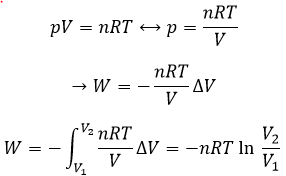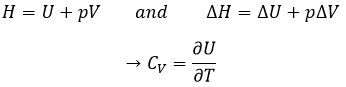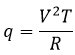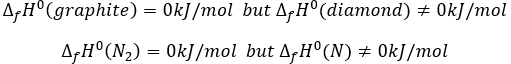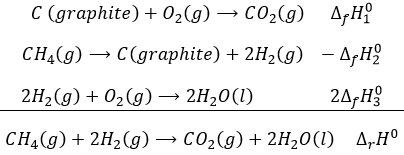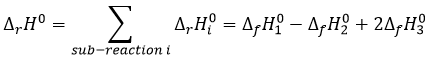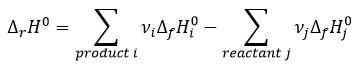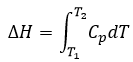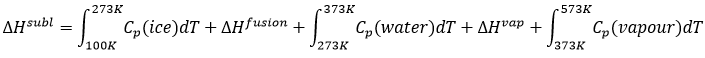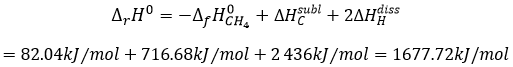La thermodynamique est l’étude du transfert de l’énergie et surtout de la chaleur. Il est important de faire la distinction entre la chaleur (q) et la température (T). La température reflète le mouvement des particules et est reliée à leur énergie cinétique mais la température n’est pas l’équivalente de l’énergie. La chaleur est une énergie qui est proportionnelle à la différence de température entre plusieurs compartiments, par convention elle va à partir du compartiment le plus chaud vers celui qui est le plus froid. Les unités de la chaleur sont les unités d’ énergie, c.-à-joules J = Nm
Quand il s’agit de transferts d’énergie nous devons définir le système dans lequel nous travaillons. Le système est la partie de l’univers que nous analysons et nous distinguons à partir de l’environnement qui est le reste de l’univers.
3 types de systèmes peuvent être définis :
– Le système isolé : il n’y a pas d’échange entre le système et l’environnement
– Le système fermé : les échanges d’énergie sont possibles entre le système et l’environnement
– Le système ouvert : les échanges d’énergie et/ou de matières sont possibles entre le système et l’environnement
Un système est exothermique s’il dégage de la chaleur. S’il prend la chaleur, le système est endothermique.
La thermodynamique est régie par trois grands principes.
Premier principe :
Conservation de l’énergie : l’énergie de l’univers est constante.
Cela signifie que le processus se produisant dans un système isolé ne comporte pas de variation de l’énergie. Si les échanges d’énergie sont autorisés avec l’environnement, par exemple dans des systèmes fermés, la variation interne de l’énergie dans un système est composé par le q de chaleur et le W de travail.
Si le système permet également les échanges de matière, un terme représentant l’énergie de l’écoulement de la matière dEm est ajoutée.
La variation de l’énergie est une fonction d’état. Cela signifie que cette fonction ne dépend pas de quelle manière le système a atteint ce point mais seulement sur son état initial et final. W et q ne sont pas des fonctions de l’Etat et dépendent de la façon dont le système évolue au cours du processus.
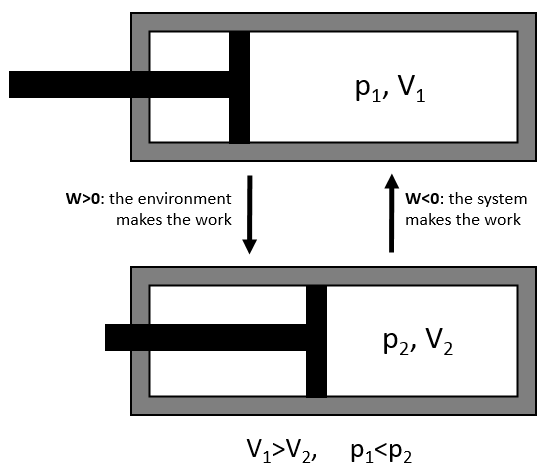
Le travail a une valeur négative si elle est faite par le système. Par exemple, imaginez un volume dans lequel un gaz est stocké.
Pour comprimer le gaz l’environnement doit appliquer une force sur le piston. W est donc positif dans ce cas. Si le piston est libre de mouvement, le gaz dans le volume applique une pression sur le piston pour augmenter le volume du système. Dans ce cas W <0.
Le travail est une énergie il est donc essentiellement une force multipliée par la distance. Si nous considérons la dilatation d’un gaz parfait le travail serait :
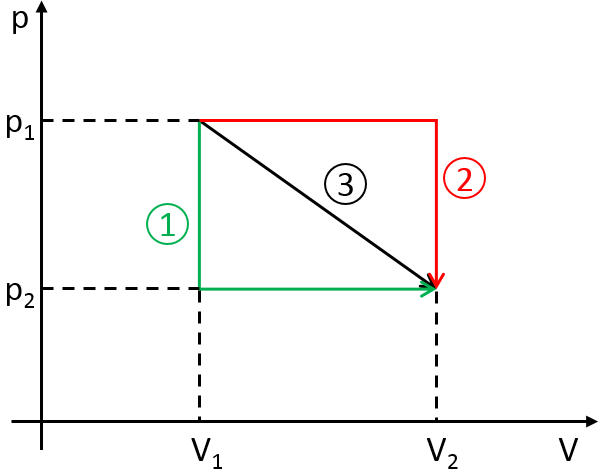
Pour passer d’un état (p1, V1) à (p2, V2) plusieurs chemins peuvent être pris.
Ces chemins sont équivalents en terme de variation de l’énergie parce que l’énergie est une fonction d’état : l’état final et les états initiaux sont caractérisés par une énergie qui ne dépend pas de la façon dont ils ont été obtenus. Pourtant le travail et la chaleur sont différents pour chaque trajet.
En effet sur le chemin 1, W = -p1 (V2-V1). Sur le chemin 2 le travail est W = -p2 (V2-V1). Comme p2 <p1, cela signifie que plus de travail est nécessaire sur la voie 1 et qu’il ya une plus grande production de chaleur sur la voie 2. Sur la voie 3 le volume et la pression varient simultanément. Nous utilisons la loi du gaz parfait pour déterminer le travail dans ce cas. Voie 3 est en fait une courbe isotherme où q = 0.
Maintenant parlons un peu de chaleur. Dans les chapitres précédents nous avons discuté à propos de la capacité de la chaleur. C’est l’énergie nécessaire pour augmenter la température du substrat par un kelvin/degré. Nous distinguons la capacité thermique à pression constante Cp et au volume constant CV.
Notez que nous avons utilisé les dérivés partiels ∂ / ∂T au lieu de dérivés d/dt. Un dérivé partiel d’une fonction de plusieurs variables est son dérivé par rapport à une de ces variables, les autres restant constants.
H est l’enthalpie de l’état et ΔH est la variation d’enthalpie du processus (qui peut être une réaction ou une transition de phase par exemple) à une pression constante. ΔH est donc équivalente à qp, l’indice p indiquant que c’est la chaleur à p = cst :
L’équation de l’enthalpie est :
Pour les gaz parfaits PV = nRT donc :
Étant donné que Cp= ∂H/∂T nous trouvons une relation entre Cp et CV des gaz parfaits :
Pour les solides et les liquides la variation de volume est négligeable et Cp»CV.
La calorimétrie :
Une enthalpie de réaction AH° est associée à chaque réaction.
Le ° indique que cette valeur est l’enthalpie trouvée pour une mole de réactif à 1 atm. Expérimentalement l’enthalpie de la réaction peut être mesurée par calorimétrie. Au cours de la calorimétrie une réaction est réalisée dans un système isolé (pas d’échanges avec l’environnement). La variation de la température dans le système est mesurée et à partir de cette mesure nous pouvons déduire la chaleur de réaction. Par exemple, la neutralisation de l’HCl par du NaOH est exothermique (AH°<0) ce qui signifie que cette réaction produit de la chaleur. Il est ainsi possible de mesurer une variation de la température ΔT pendant la réaction. Pour ce faire, nous utilisons un récipient fermé et isothermique dans lequel les réactifs sont initialement séparés. La température dans le système peut être lue sur un thermomètre. La température n’est pas directement prise dans la solution (des réactives). Habituellement la réaction a lieu dans un récipient appelé bombe calorimetrique qui est entouré par l’eau. La configuration entière est dans le recipiant isotherme. La variation de la température est mesurée dans l’eau. Lorsque la réaction a lieu l’élévation de la température est enregistrée en fonction de la quantité utilisée de NaOH. Avec le réglage adapté nous pouvons mesurer qp (p = cst) ou qV (V = cst).
Si la pression est maintenue constante la variation de la température ΔT est proportionnelle à qp.
Comme nous considérons une phase liquide qp»qV.
CV peut également être déterminée expérimentalement : une quantité de chauffage donnée est appliquée à la solution à travers une résistance électrique :
Avec la tension V et la résistance R la variation de température ΔT en raison de ce chauffage dépend de la capacité calorifique du liquide :
Donc si l’on connaît la tension appliquée et la résistance la mesure de la variation de la température donne la valeur de Cv.
Loi de Hess :
L’énergie et l’enthalpie sont des fonctions de l’état, à savoir que leur valeur ne change pas en fonction de la voie/processus et ne sont qu’une fonction de l’état du système. Cependant la loi de Hess dit que la valeur absolue de l’énergie des choses ne peut pas être déterminée seules les variations de l’énergie peuvent être déterminées. Cela signifie que l’on peut déterminer la valeur de l’enthalpie par rapport à un procédé donné et donc que l’enthalpie de formation d’une molécule est déterminée par rapport aux autres réactions.
Par convention, l’enthalpie de formation de corps simples dans leur état standard à 25°C et 1 atm est égale à 0 kJ/mole. Dans la nature certains éléments peuvent être trouvés dans plusieurs Etats mais le corps dans son état normal à 25°C et 1 atm seul a une ΔfH° = 0 kJ / mole. Par exemple
By convention, the enthalpy of formation of simple bodies in their standard state at 25°C and 1 atm equals 0kJ/mol. In the nature, some elements can be found in several states but the body in its normal state at 25°C and 1 atm alone has a ΔfH°=0kJ/mol. For instance,
Pour les molécules qui ne sont pas dans leur forme standard l’enthalpie de formation est l’enthalpie de la réaction produisant la molécule à partir des éléments dans leur état standard qui le composent.
L’enthalpie de cette réaction est donc l’enthalpie de formation du dioxyde de carbone CO2 : il est la réaction qui génère du dioxyde de carbone à partir des éléments dans leur état standard qui composent CO2.
Cette réaction est l’inverse de la formation du méthane CH4. L’enthalpie de réaction est simplement l’enthalpie de formation avec un signe(-) ΔrH°=-ΔfH°.
L’enthalpie de cette réaction est deux fois l’enthalpie de formation de l’eau parce que nous formons deux moles d’eau avec cette réaction. L’enthalpie de réaction est donnée en kJ par mole de produit.
Si nous combinons ces trois réactions nous obtenons le cycle de Hess. L’enthalpie de cette équation finale est la somme des enthalpies de formation des trois sous-réactions :
On peut résumer les enthalpies des réactions secondaires pour obtenir l’enthalpie de la réaction de formation de CO2 et H2O de CH4 et O2.
D’une manière générale, l’enthalpie de réaction est la somme des enthalpies de formation des produits moins les enthalpies de formation des réactifs chacun multiplié par ses coefficients stoechiométriques.
Nous voyons clairement ici que ces deux expressions sont identiques :
Ne pas oublier que l’enthalpie est une fonction de l’état, mais dépend de la température et que la réaction peut être favorisée par une variation de la température.
À une pression constante l’enthalpie peut donc varier en cas de variation de température
Un changement d’état va également augmenter l’enthalpie de la réaction.
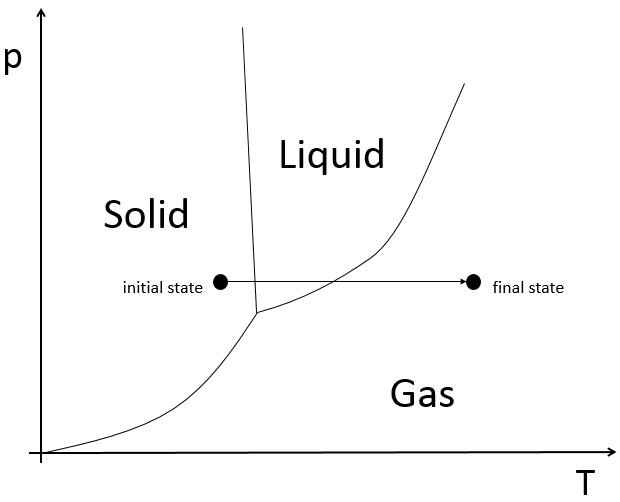
Si nous voulons changer la glace en vapeur, à savoir sublimer la glace, à une pression constante = 1 atm,
L’enthalpie sera
Le point triple est un point particulier où la glace, la vapeur et l’eau coexistent et où :
De ce point nous pouvons trouver l’enthalpie d’une transition de phase des deux autres.
L’énergie de liaisons :
Nous avons vu que nous pouvons trouver l’enthalpie deS réactions des enthalpies de formations de chaque participant de la réaction. Il devrait donc y avoir des réactions qui nous permettent de déterminer l’énergie de liaisons chimiques. Par exemple la réaction :
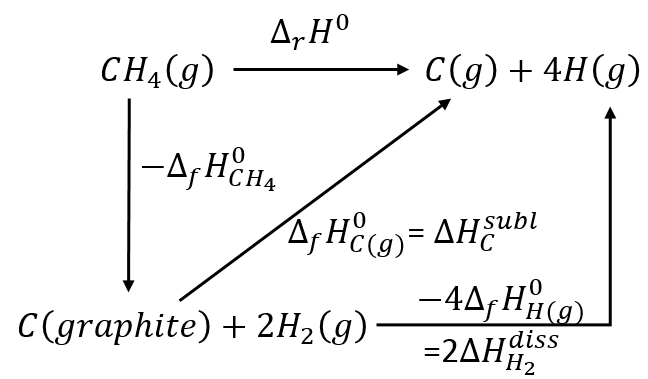
est fondamentalement la scission de 4 liaisons C-H. Rien d’autre n’a été fait au cours de cette réaction. On peut déterminer l’enthalpie de la réaction ΔrH0 de l’enthalpie de formation de CH4, C et H. On a vu plus haut l’inverse de la réaction de formation du méthane
De cette réaction nous avons encore besoin de dissocier les molécules de H2 et de sublimer le graphite dans un gaz.
Comme il ya quatre liaisons CH qui ont été brisées chaque obligation a une énergie de 419kJ / mol.
Carburants :
La thermochimie est un vaste domaine de la chimie qui trouve des applications dans les carburants par exemple. Nous pouvons déterminer l’énergie des liaisons lors de la combustion des molécules composant le carburant exactement de la même manière que nous l’avons fait pour la liaison C-H. L’hydrazine N2H4 est une molécule d’azote utilisée comme carburant pour les hélices de l’espace.
La plupart des composés azotés ont une enthalpie positive de la formation ce qui signifie que nous avons besoin de dépenser de l’énergie pour les générer. Cela signifie aussi qu’ils vont se casser facilement pour former N2 et H2O générant beaucoup d’énergie. Une exception est NH3. Quel est l’énergie de la réaction? O2 et N2 sont dans leur forme standard ce qui signifie que leur ΔfH0 = 0kJ/mol. L’enthalpie de réaction est ainsi
Cette réaction produit de la chaleur parce que l’énergie des liaisons formées est supérieure à l’énergie des liaisons cassées. Nous avons cassé 4 liaisons NH pour former 4 OH et la liaison NN devenue une liaison triple N≡N. Les liaisons OH et N≡N représentent respectivement 460kJ/mole et 941kJ/mole.
En raison de la quantité d’énergie qui a été générée par la réaction, il y a un changement de la phase et l’eau devient gaze. La propulsion de la navette spatiale est le résultat de l’énergie,qui provient de l’expansion du gaz : à partir d’une mole d’eau on fait 3 moles de gaz. Le gaz s’élargit très rapidement en raison de la chaleur (pV = nRT) générant l’explosion dans l’hélice.
Cette réaction produit de la chaleur parce que l’énergie des liaisons formées est supérieure à l’énergie des liaisons cassées. Nous avons cassé 4 liaisons NH pour former 4 OH et la liaison NN est devenue une liaison triple N≡N. Les liaisons OH et N≡N représentent respectivement 460kJ/mole et 941kJ/mole.