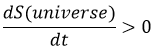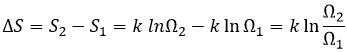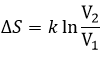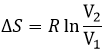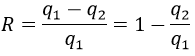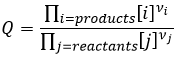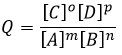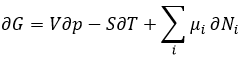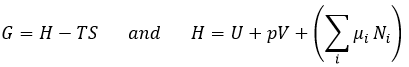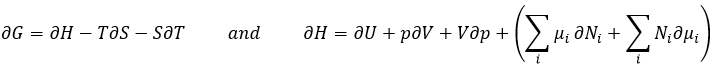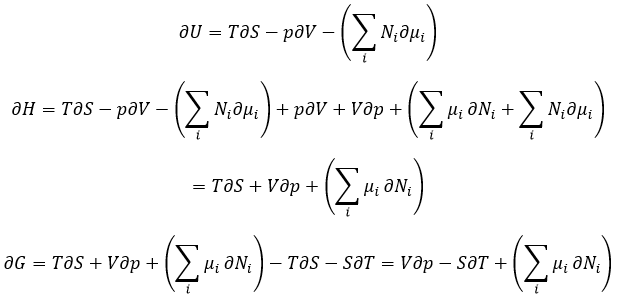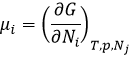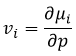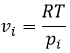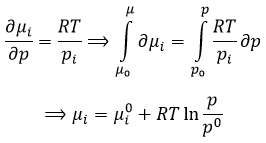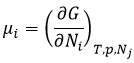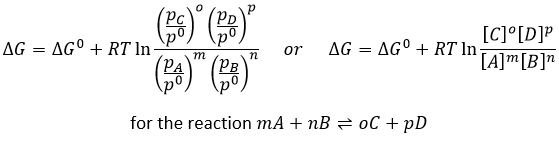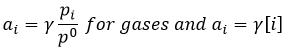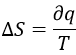Deuxième principe :
Augmentation de l’entropie: L’entropie dans l’univers augmente avec le temps.
L’entropie est une mesure du désordre d’un système. La seconde loi de la thermodynamique a plusieurs formulations mais la plus commune est qu’un processus est spontané si, sans influence externe (système isolé), il induit une augmentation de l’entropie dans l’univers.
Par exemple, si deux réservoirs sont connectés, l’un étant vide et l’autre plein de gaz, le gaz occupera spontanément tout le système même s’il n’implique aucune variation d’énergie.
Le gaz se dilate car il y a plus de positions à occuper dans un plus grand volume. Une autre définition de l’entropie est qu’un système a tendance à changer à l’état le plus probable.
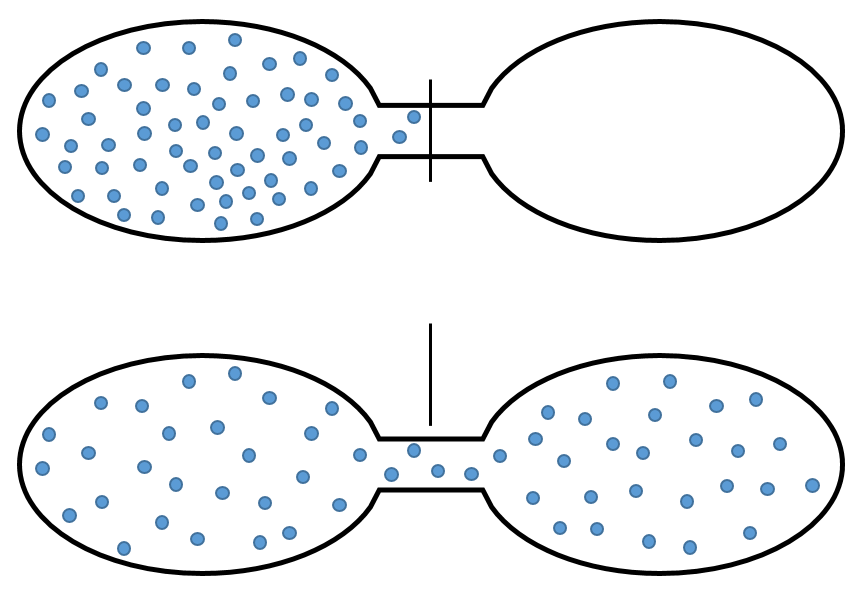
Imaginez une petite boîte avec seulement quelques positions disponibles. Deux particules sont dans cette boîte et chacune occupe une place. Plusieurs combinaisons sont possibles:
Si nous augmentons le volume de la boîte, la quantité de possibilités augmente exponentiellement. C’est une entropie de position / disposition. La formule de ce type d’entropie pour une particule est :
Ω étant la quantité de configurations possibles pour cette particule.
Si le volume contenant cette particule passe d’un volume V1 à un volume V2, la variation de l’entropie est
Le nombre de positions pour une particule est directement proportionnel au volume et
Pour les gaz dilués, le volume des particules est négligeable par rapport au volume du système. En conséquence, nous pouvons ignorer la présence d’autres particules dans la formule et dire que pour les particules NA (1 mole)
Nous avons vu plus haut la dilatation d’un gaz que l’énergie était une fonction d’état mais que le travail et la chaleur n’étaient pas et donc que la façon dont le processus se déroule a une influence sur le travail et sur la chaleur. Le troisième chemin que nous avons discuté était le processus isotherme pour lequel nous avons trouvé une expression pour le travail
Ce processus est isotherme donc ΔE = q + W = 0.
Nous pouvons donc trouver la variation d’entropie pour ce processus par la chaleur. Si le gaz se dilate, la chaleur pénètre dans le système (c’est un processus endothermique).
La variation de l’entropie est donc équivalente à la quantité de chaleur que le gaz doit absorber pour maintenir sa température constante.
Les états de la matière n’ont pas la même entropie. Un gaz a une valeur d’entropie plus grande qu’un liquide, lui-même un peu plus grande que celle d’un solide. Nous pouvons facilement comprendre cela en utilisant la répartition des particules dans une petite boîte.
Dans un gaz (parfait), les particules n’ont pas d’interactions entre elles. Ils peuvent ainsi occuper n’importe quelle position du volume sans restriction. Dans un liquide, les particules interagissent entre elles et restent groupées mais la forme de la grappe n’est pas figée. Les possibilités sont donc plus limitées que pour un gaz. Dans un solide, les particules sont fixées ensemble dans une forme donnée. Les positions qu’un solide peut prendre sont donc plus limitées que celles qu’un liquide peut prendre et beaucoup plus limitées que pour un gaz.
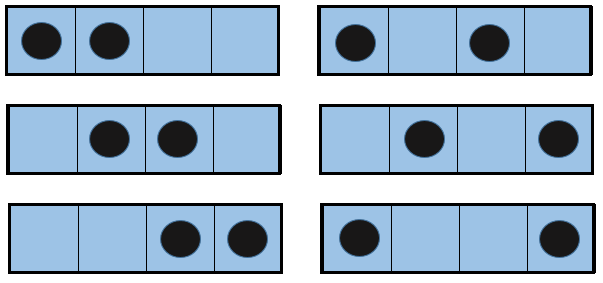
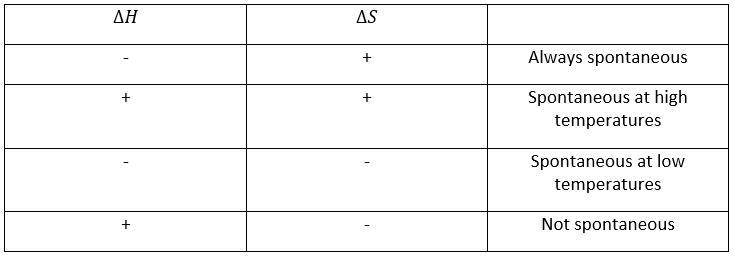
Des tables d’entropies standard existent et donnent l’entropie des molécules dans un état donné à 298K. Pour résumer, plusieurs cas peuvent être distingués. Un processus se produit si la production d’entropie dans l’univers est positive. Cette production d’entropie est composée de la variation de l’entropie dans le système et dans l’environnement. Une de ces composantes de l’entropie peut être négative si l’autre composante est positive et plus grande en valeur absolue.
Quand une réaction produit un gaz, la variation de l’entropie est positive. Si cette réaction est exothermique, la chaleur est transmise à l’environnement, ce qui signifie que son entropie augmente. Cette réaction est donc spontanée. Si la réaction était endothermique, la variation de l’entropie de l’environnement aurait été négative. La réaction pourrait encore être spontanée si la production de l’entropie de la réaction est plus grande que la diminution de l’entropie dans l’environnement.
Cycle of Carnot
Nicolas Léonard Sadi Carnot a proposé un moyen de convertir l’énergie thermique en travail. C’est un cycle thermodynamique, c’est-à-dire une série de transformations d’état ramenées à l’état initial, composées de deux processus isothermes (pas de variation de température) et de deux processus adiabatiques (pas d’échange thermique avec l’environnement). Tous les processus sont réversibles et le cycle peut donc se faire dans le sens opposé, convertissant le travail en une différence de température.
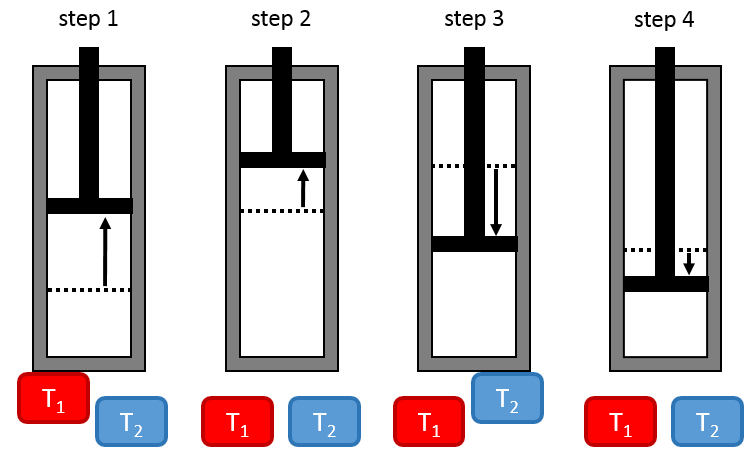
La configuration est faite d’un réservoir dont le volume peut changer et qui peut être en contact avec deux corps de température T1 et T2, T1 étant plus grand que T2.
Première étape: expansion isothermique du gaz à T1. Le réservoir est en contact avec le corps chaud à T1. La chaleur q1 est échangée entre le corps et le réservoir de gaz qui se dilate sans variation de température. Il y a donc une variation d’entropie ΔS1=q1/T1.
Deuxième étape: expansion adiabatique du gaz. Au cours de cette deuxième étape, il n’y a pas d’échange de chaleur mais le gaz continue à se dilater, à travailler sur le piston et à refroidir de T1 à T2. Le corps à T = T1 n’est plus en contact avec le réservoir. Comme il n’y a pas d’échange de chaleur, il n’y a pas de variation d’entropie.
Troisième étape: compression isothermique du gaz en T2. Le réservoir est maintenant en contact avec le deuxième corps, à T = T2, provoquant un transfert de chaleur q2 tandis qu’une compression est appliquée par le piston, gardant la température constante. Il y a donc une variation d’entropie ΔS2=q2/T2.
Quatrième étape: compression adiabatique du gaz. Le corps à T = T2 n’est plus en contact et il n’y a pas de transfert de chaleur possible. Le gaz continue à diminuer en volume tandis que sa température change de T = T2 à T = T1. A la fin de cette étape, le système est de nouveau dans les conditions (volume, température et pression) de l’état initial.
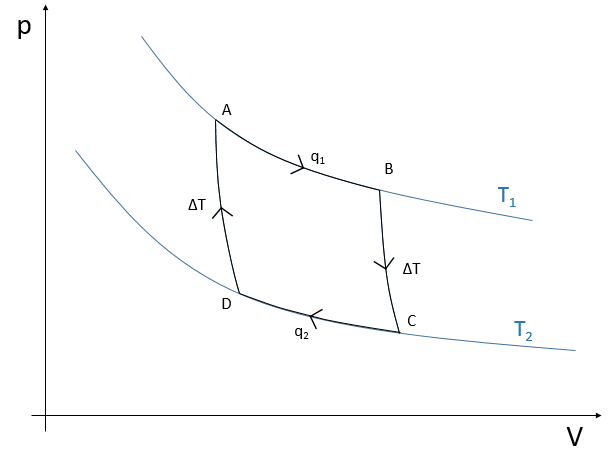
Le cycle peut être tracé dans le diagramme de phase pV comme indiqué ci-dessous:
L’efficacité R = W/q1 du cycle de Carnot serait de 100% si tout le travail W était transformé en chaleur q. Le travail ici est la différence de chauffage q1-q2 car ΔE = 0 = q + W (système isolé, les corps en T1 et T2 étant dans le système). Par conséquent,
Il est possible de montrer que le rapport q2/q1 est égal au rapport T2/T1.
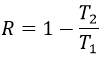
La conséquence est que l’efficacité n’est jamais à 100% sauf à T2 = 0K, que nous ne pouvons pas atteindre sur terre. La perte d’énergie est causée par la production d’entropie.
Energie libre de Gibbs :
Pour qu’une réaction se produise, nous venons de voir que deux facteurs sont importants: l’enthalpie de réaction (si la réaction est exo ou endothermique) et la variation d’entropie. L’énergie libre de Gibbs ΔG regroupe les deux facteurs dans une équation
Une réaction est spontanée si ΔG <0. Le terme entropique montre clairement qu’une réaction peut être spontanée à une température donnée mais pas si la température est modifiée
Nous pouvons trouver des tables pour des valeurs standard de ΔH0 et ΔS0 et des tables de ΔG0 pour les réactions de formations de molécules. A d’autres températures mais à 1 atm, la relation est :
Q est le quotient réactif que nous avons déjà rencontré précédemment :
Par exemple, le quotient réactif de cette réaction
est:
Si AG est négatif, la réaction va vers la droite, si elle est positive, les réactions vont vers la gauche. Si ΔG = 0, nous sommes à l’équilibre. En conséquence, nous pouvons trouver une relation reliant la constante de l’équilibre K avec l’énergie libre de Gibbs:
Le potentiel chimique :
Le potentiel chimique μi est l’énergie d’une molécule i qui peut être utilisée lors d’une réaction ou d’un processus physique.
Équation de Gibbs-Duhem:
Le dernier terme est donc une variation d’énergie dans le système due à une variation des quantités de particules dans le système, ce dont nous n’avions pas tenu compte auparavant (il sera montré entre parenthèses dans les équations suivantes). La relation ci-dessus vient des définitions de G et de H:
Les dérivées partielles de ces fonctions sont
Nous avons vu que l’énergie interne ∂U=∂q+∂W-(∑iNi∂μi) et que ∂S=∂q/T et que ∂W=-p∂V. Par conséquent.
Le potentiel chimique est donc la variation de l’énergie libre de Gibbs en ce qui concerne la variation de concentration d’une espèce spécifique, en gardant les autres paramètres (p, T et les concentrations des autres espèces) constants.
Nous définissons également le volume molaire partiel
c’est utile pour les gaz. De la loi des gaz parfaits,
Cela nous conduit à l’expression du potentiel chimique pour un gaz
En solution, la formule est très similaire
Nous savons que
On peut donc trouver l’expression de ΔG en fonction des pressions ou des concentrations de l’espèce:
Pourtant, cela n’est vrai que pour les solutions idéales et les gaz. Normalement, nous devons considérer l’activité de chaque molécule
γ est égal à 1 pour les solutions idéales mais peut varier si les concentrations augmentent, ce qui représente l’augmentation des interactions entre les espèces. Cependant, l’activité a des solides est égale à 1.
Troisième principe :
L’entropie d’un cristal parfait au zéro absolu est exactement égale à zéro.
La troisième loi fournit une référence pour l’entropie de tout cristal pur (et donc de n’importe quoi) à n’importe quelle température. Un cristal parfait et pur est un cristal dont l’arrangement est parfaitement organisé: il n’y a pas de défaut, la matrice est régulière et elle est composée d’une seule espèce. Au zéro absolu, c’est-à-dire zéro Kelvin, l’état du système est à l’énergie minimale possible. Cet état est unique du fait de la mécanique quantique et c’est bien le cas: il n’y a qu’une seule façon de placer les atomes dans un cristal parfait. La quantité de configurations possibles est donc 1, conduisant à une entropie égale à
Si un état de base est dégénéré, c’est-à-dire qu’il y a plusieurs états de même énergie, il y a plusieurs configurations possibles Ω et l’entropie n’est pas égale à 0 mais elle est très proche de celle-ci. Dès qu’il y a un défaut dans le cristal, le nombre de configurations possibles augmente. En conséquence, l’entropie augmente. Cette variation d’entropie est synonyme de variation d’énergie comme le dit la deuxième loi
L’augmentation de température dT due à la chaleur ∂Q est déterminée par la capacité calorifique (cp ≈ cV) du cristal
Conséquences de la troisième loi
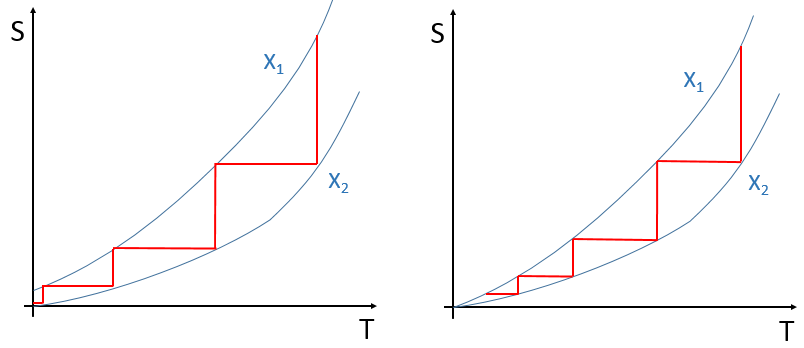
Une première conséquence de la troisième loi est que T= 0K ne peut être atteint par un nombre quelconque de processus finis. Cela est dû au fait qu’il n’y a qu’un seul état d’énergie minimale. Si nous essayons de changer de façon contrôlée un paramètre donné pour que l’énergie diminue à chaque fois, il faudrait un nombre infini de répétitions pour atteindre le zéro absolu. C’est un peu similaire au problème de la balle: si à chaque période de temps une balle se déplace de la moitié de la distance nécessaire pour atteindre sa cible, la cible sera approchée mais jamais atteinte. Si plusieurs états étaient autorisés à T= 0K, il serait possible de basculer le paramètre pour obtenir l’un ou l’autre état: une valeur du paramètre s’approche du système d’un état et l’autre approche du système de l’autre état. Avec une seule cible, nous ne pouvons pas passer d’une valeur du paramètre à l’autre et atteindre l’état final. Nous pouvons visualiser ceci comme ceci :
Une deuxième conséquence est que les capacités calorifiques cp et cV tendent vers zéro lorsque T tend vers zéro.