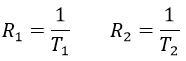Une section complète peut être (et sera) dédiée à la mise en place détaillée de la résonance magnétique nucléaire (RMN) et aux analyses que nous pouvons effectuer avec cet outil. Dans ce chapitre, nous n’avons pas besoin de beaucoup d’explications sur la théorie de la RMN car c’est une section orientée technique. Nous donnerons cependant une introduction sur la RMN appliquée au proton mais gardons à l’esprit que beaucoup plus peut être fait.
Principe de la RMN
De même que pour la spectroscopie, lorsqu’un champ magnétique est appliqué sur un échantillon, une partie des rayonnements électromagnétiques peuvent être absorbés, dont les fréquences dépendent des propriétés de l’échantillon. Un spectre RMN donne des pics d’intensités diverses en fonction de la fréquence d’absorption. Les atomes ont des réactions différentes résultant de l’application du champ magnétique et absorbent dans des régions séparées de fréquences ou n’absorbent pas du tout. Mais plus important encore, et c’est ce qui nous intéresse dans cette section, la fréquence d’absorption d’un atome dépend de son environnement direct. Par exemple, nous pouvons détecter la différence d’absorption pour les atomes d’hydrogène situés à l’extrémité de la chaîne et à l’intérieur de la chaine dans la molécule suivante CH3-CH2-CH3 (δ≈0.91, 1.34, 0.91).
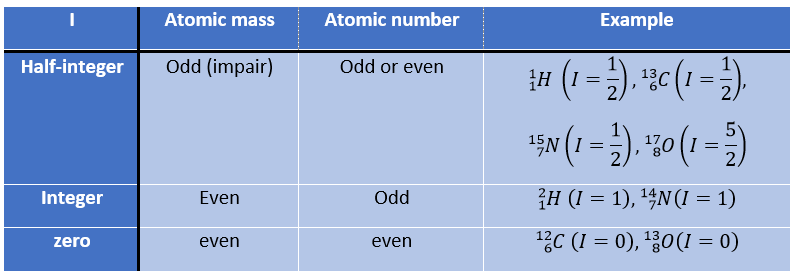
Premièrement, revenons à l’absorption de différents atomes. Tout noyau porte une charge électrique mais dans certains d’entre eux cette charge tourne dans une direction donnée autour de l’axe nucléaire. Ce mouvement induit un dipôle magnétique qui peut être décrit en terme de nombre de spin nucléaire I. Je peux avoir n’importe quelle valeur positive à partir de 0 et par étape de ½, soit 0, ½, 1, 3/2, 2, … Un isotope a une valeur de spin qui dépend de la masse atomique et du nombre d’isotopes. Nous pouvons reprendre de cette façon:
Le nombre de spin détermine le nombre d’orientations qu’un noyau peut prendre dans un champ magnétique externe uniforme, suivant la formule n = 2I + 1. Un atome avec I = 0, tel que le carbone 12, ne peut donc prendre qu’une orientation et est « inactif » en RMN. Les atomes avec I≥1 ont une répartition non sphérique de la charge décrite par un moment quadripolaire qui affecte les noyaux voisins.
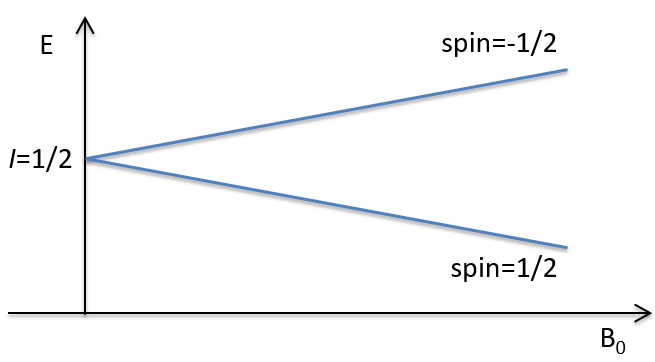
Les atomes avec I = 1/2, tels que 1H et 13C peuvent prendre 2 orientations avec des énergies différentes correspondant au spin +1/2 et -1/2. Le niveau d’énergie inférieure a un petit excès de population qui dépend de l’intensité du champ magnétique appliqué.
Les atomes avec I=1/2, tels que 1H et 13C peuvent prendre 2 orientations avec des énergies différentes correspondant au spin +1/2 et -1/2. Le niveau d’énergie inférieure a un petit excès de population qui dépend de l’intensité du champ magnétique appliqué.
Pour faire la transition entre les deux niveaux, les quanta d’énergie hν, avec ν la fréquence du rayonnement électromagnétique, sont nécessaires dans un champ magnétique B0. La fréquence est liée au champ magnétique par la relation :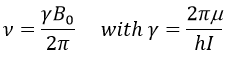
γ est la constante gyromagnétique qui dépend du spin I et du moment magnétique μ. Sachant cela, le problème est de trouver un moyen de transférer cette énergie et de mesurer l’énergie absorbée.
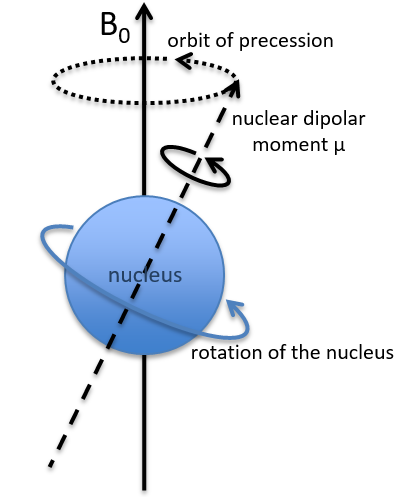
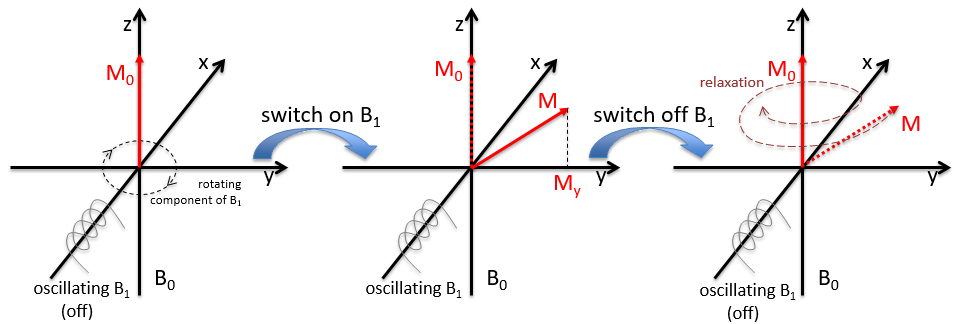
Dans un champ magnétique, un proton tourne sur lui-même et autour de l’axe du champ magnétique (voir la figure suivante).
La vitesse de précession ω0, aussi appelée fréquence de Larmor est égale au produit de la constante gyromagnétique γ avec l’intensité du champ magnétique B0.
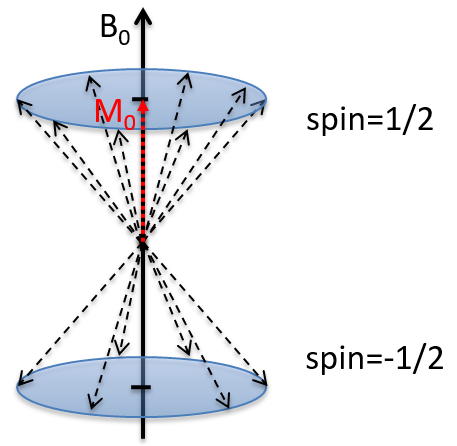
A cause du champ magnétique, tous les atomes sont orientés dans la même direction mais ils ne sont pas au même stade de la précession. Selon le spin, l’orientation est parallèle au champ (spin = 1/2) ou antiparallèle (spin = -1/2). Comme il y a un petit excès de population pour le spin = 1/2, une aimantation globale M0 est dans l’axe de B0 (axe z) mais il n’y a pas de magnétisation particulière dans les autres directions (axes x-y).
Nous inclinerons la magnétisation vers le plan horizontal en utilisant un oscillateur qui génère un second champ magnétique B1 perpendiculaire à B0. Le champ électromagnétique résultant tourne à la même vitesse que le proton. Nous pouvons détecter la composante magnétique générée dans ce plan (My par exemple) si vous le souhaitez. Maintenant que le noyau est excité, nous fermons le champ magnétique B1 et laissons le noyau se détendre jusqu’à sa magnétisation précédente.
Deux méthodes de relaxation existent. La première est appelée relaxation spin-réseau ou relaxation longitudinale et implique le transfert de l’énergie des noyaux aux molécules voisines. Cette relaxation prend un temps T1. Le deuxième mécanisme de relaxation est la relaxation spin-spin, ou relaxation transversale et implique le transfert d’énergie d’un noyau à un second. Il a un temps caractéristique T2. Nous pouvons définir R1 et R2 comme :
Pour obtenir un spectre de RMN, on scanne soit la fréquence de l’oscillateur B1 soit celle du champ magnétique B0.