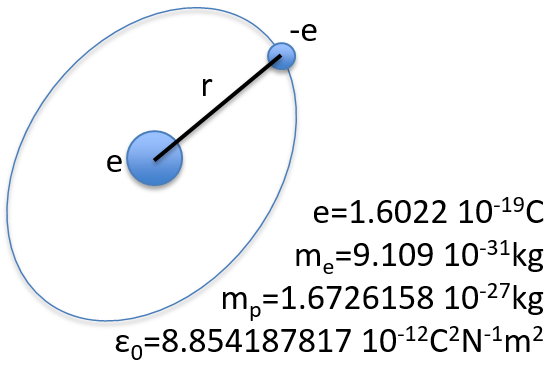
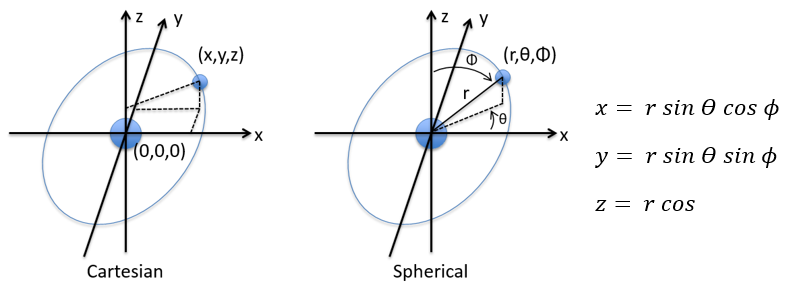
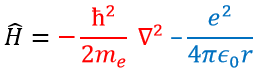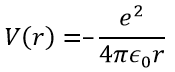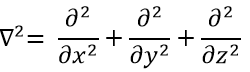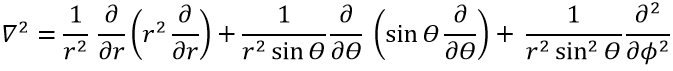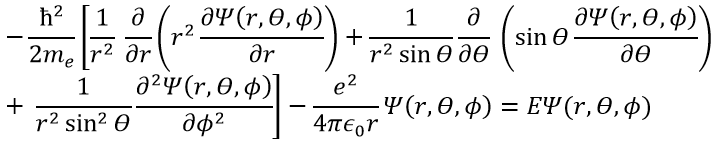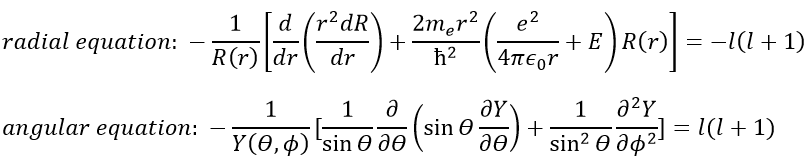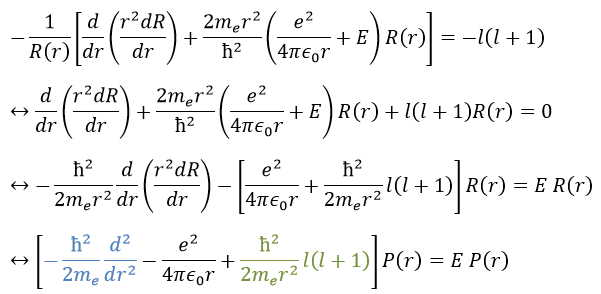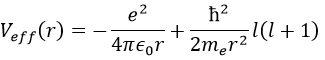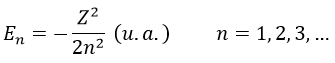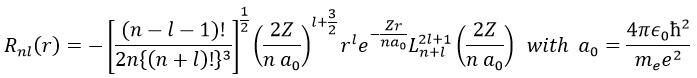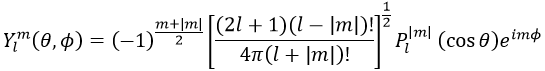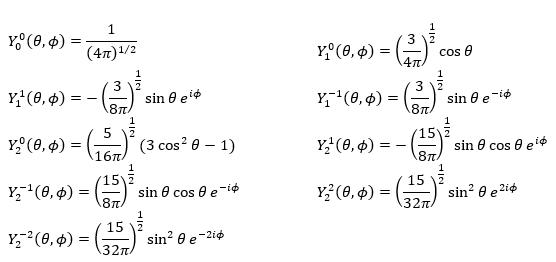Pour commencer doucement, nous décrirons la molécule non chargée la plus simple: l’hydrogène. Il est composé d’un proton avec une charge positive e et un électron de charge opposée -e qui tourne autour du proton à une distance r.
En mécanique quantique, le système est décrit par l’équation de Schrödinger
Ψ est une fonction d’onde et Ĥ est l’hamiltonien, composé d’un terme cinétique et d’un terme potentiel.
Le terme potentiel est le potentiel d’attraction entre deux charges opposées dans le vide (ϵ0 est la permittivité du vide).
Le terme cinétique décrit le mouvement de l’électron en orbite autour du noyau, où ћ=h/2π et le gradient ∇ est
en coordonnées cartésiennes. Il est intéressant de changer pour les coordonnées sphériques. L’expression semble plus complexe mais permet de séparer certaines expressions.
Alors
Cette expression semble plus complexe que la précédente, mais il y aura un gros avantage. L’équation de Schrödinger devient
Cette équation, développée, donne
En conséquence, la fonction d’onde peut maintenant être séparée en une équation radiale et une équation angulaire.
La solution des équations est directement liée au nombre quantique l. Pour rappel, les nombres quantiques n, l et m donnent la configuration électronique des atomes avec l entre zéro et n (O ≤ l ≤ n) et m entre -l et l (-l ≤ m ≤ l). Par exemple si n = 2, l peut avoir une valeur de 1 ou 0, donnant 3 valeurs possibles pour m: -1, 0 (deux fois), 1. Fermi nous dit que nous pouvons mettre 2 électrons de spin opposé sur chaque orbitale. Pour les atomes, les orbitales sont notées s, p, d, f, g, … pour l = 0, 1, 2, 3, 4, … précédées du nombre quantique n.
Nous allons d’abord essayer de résoudre l’équation radiale. Pour ce faire, nous multiplions tout par ћ2/2mer2 et changeons la variable de R(r) to P(r)=rR(r).
Il y a trois termes dans l’équation: l’énergie cinétique radiale, le potentiel de Coulomb et le terme centrifuge. L’équation est similaire à l’hamiltonien initial, mais il existe un terme de centrifugation supplémentaire. Le terme potentiel est maintenant composé d’un terme de Coulomb (potentiel d’attraction) et du terme centrifuge.
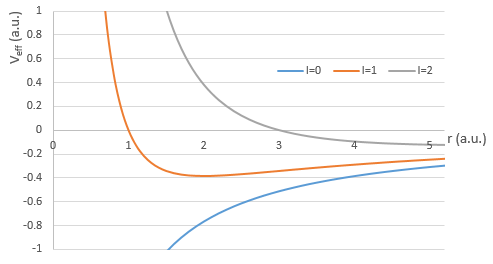
Si nous considérons le potentiel effectif, nous voyons que le terme centrifuge repousse les électrons du noyau. Les orbitales s (l = 0) n’ont pas de terme centrifuge et leurs électrons sont donc proches du noyau. Les autres orbitales impliquent un terme centrifuge positif éloignant les électrons du noyau.
L’énergie En des orbitales dépend de n et pas de l ou m.
Elle est proportionnelle à 1/n2. Les orbitales sont donc de plus en plus proches les unes des autres quand n augmente. L’énergie est négative et tend vers zéro pour n → ∞, c’est-à-dire l’ionisation. L’énergie est également proportionnelle au carré du nombre atomique. L’énergie est donc différente pour H ou He+, ou n’importe quel atome avec un seul électron malgré la structure similaire.
La solution pour la fonction d’onde est :
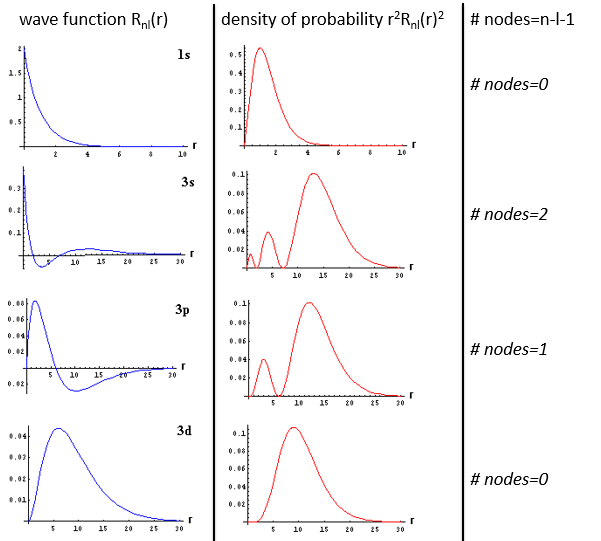
La fonction d’onde Rnl(r) dépendra donc des nombres quantiques n, l, du nombre atomique et du rayon. Dans le cas des orbitales s, la fonction d’onde n’est pas égale à zéro à r = 0. Pourtant, la densité de probabilité est r2.Rnl(r)2 et il n’y a donc pas d’électron dans le noyau.
Comme la densité de probabilité est le carré de quelque chose, les zones avec une valeur négative de Rnl(r) peuvent posséder des électrons. Les points où la densité de probabilité est égale à zéro sont appelés nœuds et leur nombre est égal à n-l-1. Notez qu’il n’y a donc pas de rayon fixe pour un électron mais pour sa plus grande probabilité de présence et que même si l’énergie des orbitales est égale, les électrons ne sont pas à la même distance du noyau. Pour les atomes mono-électroniques, les orbitales 3s et 3p sont donc à la même énergie. Ils sont dégénérés. C’est le cas pour toutes les orbitales de même valeur de n.
Maintenant, regardons la fonction d’onde angulaire Y.
où Pl∣m∣(cos) sont les fonctions associées de Legendre. La solution ici ne dépend pas de n mais de l et m. Quelques solutions sont données ci-dessous:
La première fonction d’onde angulaire Y00 donne une sphère car elle n’a aucune dépendance sur les angles et ϕ . Les autres fonctions ont des formes différentes qui dépendent des angles.
Pour obtenir des orbitales atomiques, il suffit de combiner les fonctions d’onde angulaire et radiale. Les orbitales sont sphériques. Il y a 3 orbitales p car il y a 3 valeurs possibles pour m: -1, 0 ou 1. Les orbitales sont identiques mais pointent dans des directions différentes. En fait c’est un peu plus compliqué: les fonctions d’onde angulaire pour m = -1 et 1 ont un terme imaginaire dont on se débarrasse par un changement de coordonnées, revenant aux cartésiennes. Nous pouvons faire ce changement avec une combinaison des orbitales. Nous pouvons dessiner les orbitales avec la technique suivante:
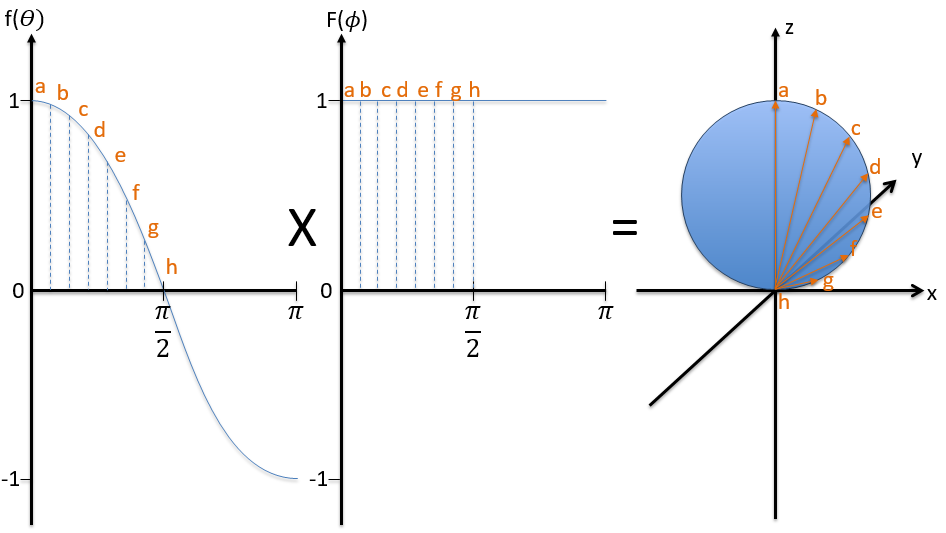
Nous prenons d’abord les fonctions qui dépendent d’un angle et dessinons leur valeur en fonction de l’angle. Pour l’orbital pz les fonctions sont f()=cos et F(ϕ)=1. Quand F = 1 pour n’importe quel angle, f va de 1 à -1. L’orbitale est donnée par la multiplication des deux fonctions. F = constant signifie que l’orbitale est identique pour toute valeur de ϕ. L’axe z est donc un axe de symétrie et l’angle dans la direction z. Quand = 0 (point a), nous sommes sur l’axe z et l’intensité est 1. Quand> 0, nous ne sommes pas sur l’axe. L’intensité est inférieure à un, donc nous dessinons un point à une plus petite distance du centre que le point précédent. L’intensité continue de diminuer pour atteindre zéro à=π/2 (point g), l’intersection avec le plan x = 0, y = 0. En fait, nous avons dessiné une sphère au-dessus du plan x = 0, y = 0. La même chose est faite de l’autre côté du plan (π/2 <<π). Cette partie de l’orbitale a un signe négatif car la fonction est négative (cos <0). Nous pouvons répéter cette méthode pour les autres directions.