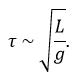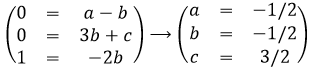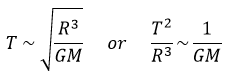Chapitre 2: quantités et unités

Les unités sont nécessaires pour évaluer les quantités. Évidemment, un rhinocéros est plus lourd qu’un chien, mais pour savoir de combien, nous avons besoin d’unités de référence. De plus, les rhinocéros n’ont pas tous le même poids. Nous avons donc besoin d’une unité cohérente pour mesurer le poids des objets. Le même problème se pose pour toutes les mesures possibles: nous ne mesurons pas avec précision la distance par rapport à la longueur des bananes car les bananes n’ont pas une longueur constante et il n’est pas pratique pour de nombreux pays d’utiliser cette unité de mesure . Les hommes ont donc défini certaines quantités comme des références, des quantités constantes quel que soit le temps ou les conditions externes (si elles ne sont pas explicitement décrites). Notez que certaines unités de mesure inexactes sont toujours utilisées dans les activités quotidiennes lorsque la précision n’est pas si importante. Par exemple, lors de la cuisson, nous ajoutons x cuillères d’huile sans donner explicitement le poids ou le volume requis.

D’autre part, nous pouvons mesurer une distance en mètres ou en miles, le poids en grammes ou en livres. Toutes ces unités ont une valeur bien définie et peuvent servir d’unités de référence. Alors que certains pays comme le Royaume-Uni ou les États-Unis utilisent des unités différentes, les conventions internationales définissent un système international d’unités (unités de base SI). Leur plus grand avantage est la relation simple entre les unités de différentes quantités. Dans le SI, un millilitre d’eau occupe un centimètre cube, pèse un gramme et nécessite une calorie d’énergie pour chauffer d’un degré centigrade, soit 1% de la différence entre son point de congélation et son point d’ébullition. Dans le système américain, vous devrez faire d’énormes calculs pour calculer la quantité d’énergie nécessaire pour faire bouillir un gallon d’eau à température ambiante, car vous ne pouvez relier directement aucune de ces quantités.

Le Bureau international des poids et mesures (Bureau international des poids et mesures) est une organisation intergouvernementale créée pour maintenir le Système international d’unités (SI) aux termes de la Convention du Mètre (Convention du Mètre, 20 mai 1875). L’organisation est généralement désignée par son initialisme français, le BIPM. Son rôle est de :

– établir des normes et des échelles fondamentales pour la mesure des grandeurs physiques principales et pour conserver les prototypes internationaux;
– comparer les normes internationales avec les normes nationales;
– assurer la coordination des techniques de mesure correspondantes;
– mesurer et coordonner les mesures des constantes physiques fondamentales impliquées dans les activités ci-dessus.

Les unités SI :

Les définitions des unités de référence sont principalement faites pour leur donner une valeur bien connue et fixe.

Ces définitions fixent la vitesse de la lumière c à 299792458 m/s et la perméabilité du vide μ₀ à 4π 10^-7 H/m exactement. Ils ont aussi parfois besoin de quelques précisions. Par exemple, nous signalons que l’atome de césium est au repos et que les atomes de carbone ne sont pas connectés, sont au repos et dans leur état fondamental.

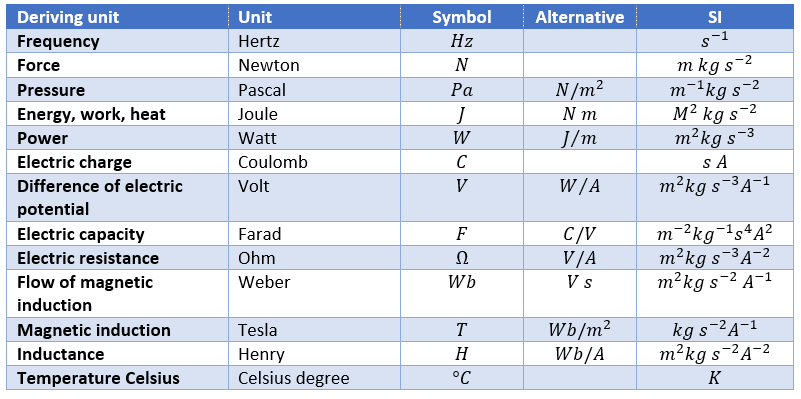
Unités dérivées :

Par facilité, certaines unités sont la combinaison des unités SI pour exprimer les unités fréquemment utilisées.

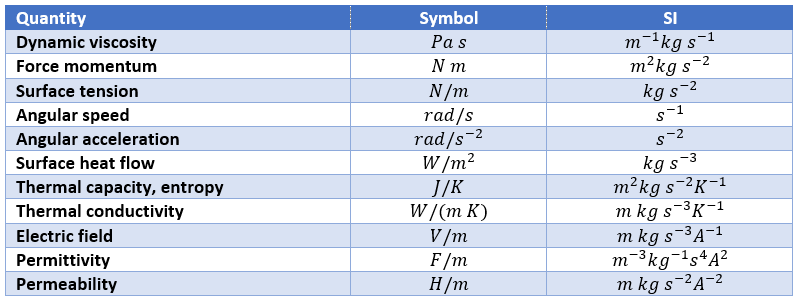
Enfin, il y a des quantités sans noms d’unités spécifiques.

Nous pouvons signaler quelques unités spécifiques:

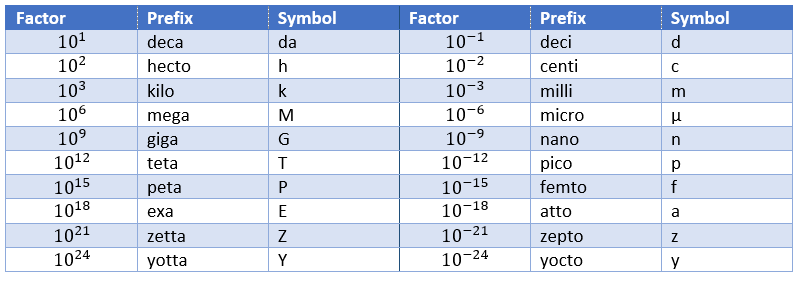
Pour mettre fin à cette section, nous listerons le préfixe des multiples des unités SI.

Analyse dimensionnelle :

L’existence du système IS signifie que toutes les autres grandeurs physiques ont des unités qui sont des fonctions homogènes de ces unités de base. Une fonction est homogène si, faisant un changement d’échelle sur toutes ses variables: x₁ → λ₁x₁, x₂ → λ₂x₂, x₃ → λ₃x₃, … la fonction elle-même change d’échelle : f(λ₁x₁, λ₂x₂, λ₃x₃,…) = λ₁^α1 λ₂^α2 λ₃^α3…f(x₁, x₂, x₃,…). Les unités de n’importe quelle quantité, appelons-le Q_r est donc toujours exprimée par une relation comme :

Donc, si nous connaissons les unités d’une quantité physique, et admettons qu’il y a une relation entre cette quantité et d’autres variables, et connaissant les unités de ces variables, nous pouvons deviner la relation entre les quantités.

Par exemple, nous observons le balancement d’un objet attaché à une corde: un pendule. Le pendule oscille parce qu’il tombe et il est retenu par la ficelle. Nous voulons déterminer la relation entre les temps pris par le pendule pour faire une oscillation, c’est-à-dire la période, avec les paramètres que nous supposons importants: la masse M de l’objet, la longueur L de la chaîne et l’accélération gravitationnelle g chaque objet sur la planète. Les unités des variables sont kg pour la masse, m pour la longueur et m/s² pour l’accélération. La période est un temps et donc son unité est s. La relation entre les variables et la période devrait être quelque chose comme ceci:

Comme il n’y a pas de kg à la gauche de l’égalité, et il est présent du côté droit de l’équation avec l’exposant a, alors nous concluons que a = 0. En regardant les secondes, leur exposant est 1 à gauche et -2b à droite, b est donc b = -1 / 2. Enfin, il n’y a pas m à gauche tant qu’il est présent du côté droit de l’équation, donc 0 = b + c. Comme nous avons déterminé la valeur de b, nous avons que c = 1/2 et que la relation globale est:

De notre analyse dimensionnelle, nous avons déterminé que la masse de l’objet n’a aucune influence sur la période d’oscillation du pendule. Notez que nous n’avons pas écrit le signe égal: l’analyse dimensionnelle ne donne pas la vraie loi; il donne des indices sur les variables mais il peut encore y avoir des facteurs numériques qui peuvent être déterminés expérimentalement. D’autre part, l’analyse dimensionnelle permet d’identifier les mauvaises lois ne respectant pas les unités des quantités.

Analysons un deuxième exemple: la période T de révolution des planètes autour du Soleil. Nous identifions d’abord les paramètres importants impliqués dans le problème: la masse M du Soleil, la distance R entre la planète et le Soleil, et une constante G donnant la force gravitationnelle. Les unités des paramètres sont respectivement kg, m et kg^-1m³s^-2. La période est donnée en secondes s. La loi devrait avoir la forme T ~ M^aG^bR^c. Pour les unités, nous avons la relation