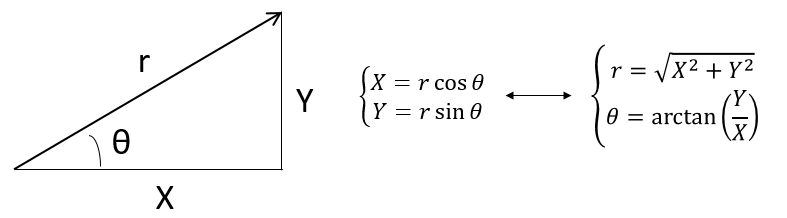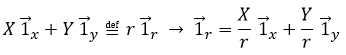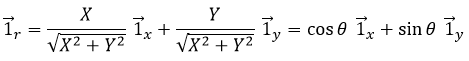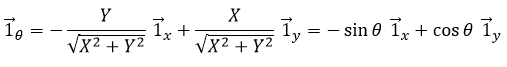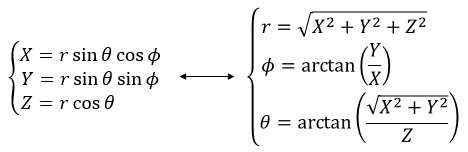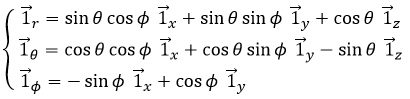Le premier formalisme qui doit être connu en physique est le formalisme du mouvement. Un formalisme est associé à une certaine méthode mathématique rigoureuse, définissant des symboles et des règles qui sont communément acceptés, dans le but que tout le monde comprenne immédiatement le sujet discuté. Nous ne nous intéresserons pas à la prédiction du mouvement ni à sa cause, mais seulement à sa description.
Dans cette section, nous considérons que chaque objet peut être considéré comme un point sans volume.
La position :
Le mouvement est l’historique de la position d’un objet, la succession des positions de cet objet sur le temps. Pour définir la position de l’objet, nous avons besoin d’un système de référence dans lequel nous pouvons donner la position: coordonnées. Plusieurs systèmes de référence existent et il existe plusieurs façons de calculer les coordonnées des objets. Tous sont corrects mais certains sont plus pratiques que d’autres. Lors d’un voyage, vous ne donnerez pas votre position à l’égard du soleil, il en est de même en physique.
Plusieurs coordonnées sont généralement nécessaires pour déterminer la position exacte d’un objet. Si vous dites que vous êtes à 10 km de Paris, vous donnez une information sur votre position mais il nous manque au moins une coordonnée pour déterminer votre position. Habituellement, vous avez besoin d’une coordonnée par dimension du système.
Une dimension :
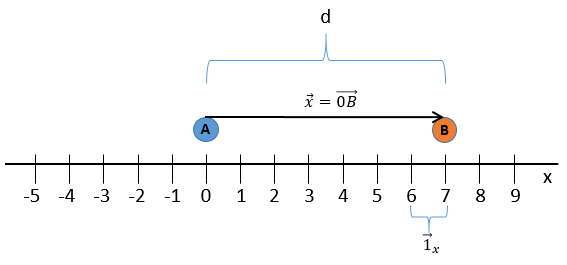
Nous choisissons une origine pour le système de coordonnées, le point zéro. Il est commode de choisir la position initiale de l’objet A comme origine mais ce n’est pas obligatoire. Ensuite, nous choisissons une direction qui sera les positions positives. Dans la direction opposée, nous avons les positions négatives. Toujours par commodité, les positions positives sont placées dans la direction vers laquelle nous devinons que l’objet se dirigera. Imaginez que l’objet se déplace vers un autre objet B placé à une distance d. Le vecteur de position indique la distance entre un objet et l’origine, et pointe vers l’objet avec une flèche. Le symbole des vecteurs est surmonté d’une flèche pointant vers la droite. Le vecteur de position pour B est
Où est le vecteur unité dans la direction x (la direction unique dans ce problème).
où 
est le vecteur unité dans la direction x (la direction unique dans ce problème).
Deux dimensions :
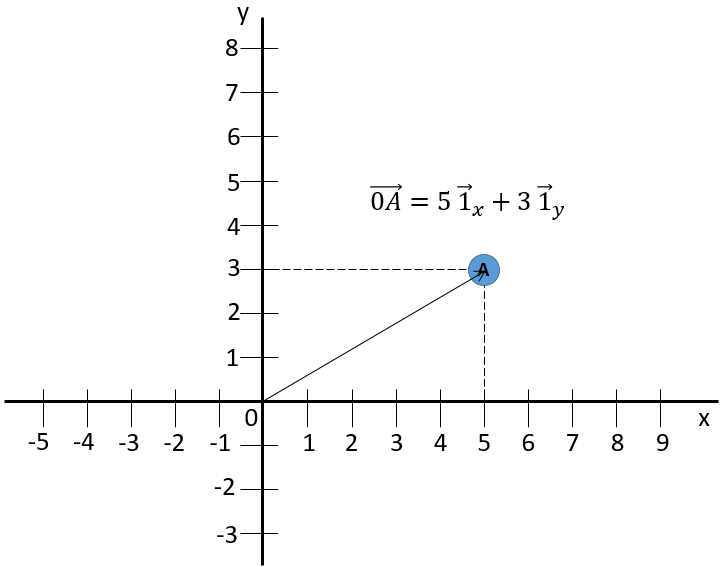
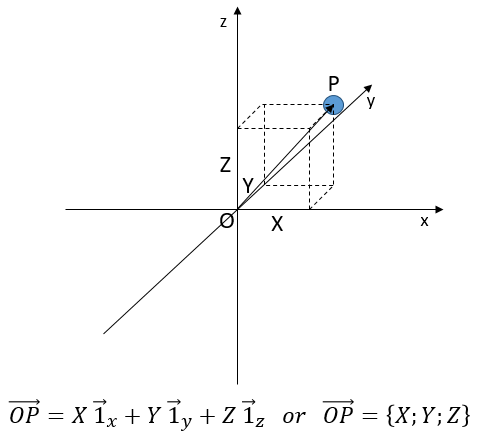
La deuxième coordonnée est généralement orthogonale, perpendiculaire à la première coordonnée pour éviter un maximum de problèmes d’angle et pour bénéficier de la simplicité du calcul pour les triangles rectangles. Chaque coordonnée, a une direction. Le vecteur de position est maintenant défini par deux composants à partir desquels nous pouvons calculer sa longueur.
Le signe d’addition entre les deux vecteurs unitaires est comme ci-dessous et non comme l’addition de deux nombres usuels. Une autre façon d’écrire des coordonnées est de les mettre entre parenthèses. Si nous faisons cela, nous n’écrivons pas les vecteurs unitaires.
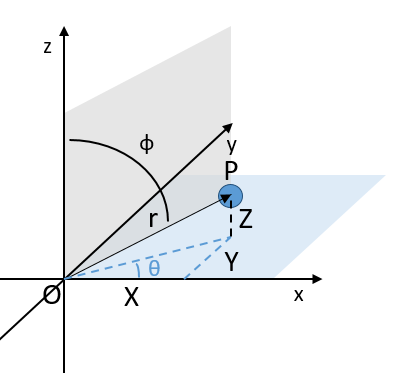
Ce système de référence, le système cartésien, n’est pas le seul qui puisse être utilisé (à deux dimensions pour déterminer la position d’un objet). Nous pouvons également positionner l’objet de sa distance r au point d’origine et un angle θ d’un axe. Ce système de référence est appelé le système polaire.
Il est possible de déterminer la relation entre les coordonnées X; Y dans le système cartésien et r; θ dans le système polaire en utilisant la relation définissant le cosinus, le sinus et la tangente:
Le vecteur d’unité 
peut ainsi être calculé.
ou
Nous pouvons également définir le vecteur de l’unité 
:
Les deux vecteurs d’unité polaire dépendent donc de θ qui doit donc être choisi consciencieusement.
Trois dimensions :
Une troisième coordonnée est ajoutée dans les systèmes de référence. Dans le système cartésien, nous ajoutons une coordonnée orthogonale aux deux précédentes
Dans le système polaire, nous avons besoin d’un second angle pour déterminer la position d’un objet. Nous prenons le premier de l’axe x dans le plan xy et le second angle est pris de l’axe z dans le plan zr de l’objet.
Encore une fois, le système cartésien peut être associé au système polaire.
Les vecteurs unitaires sont définis comme :
