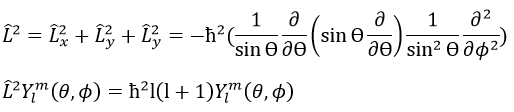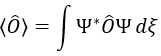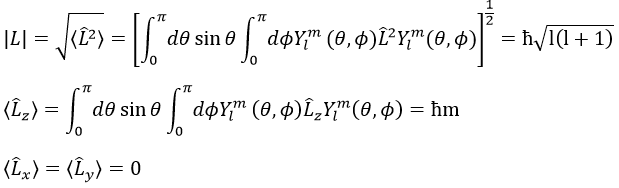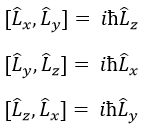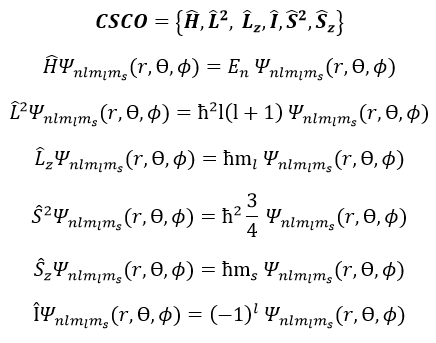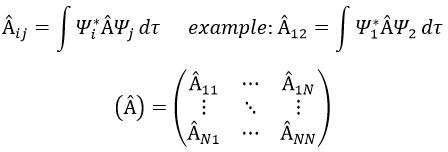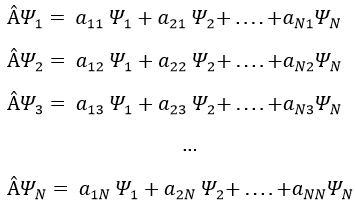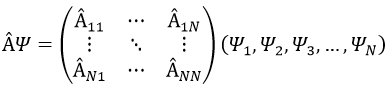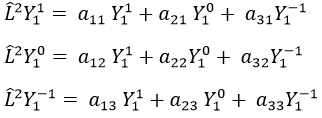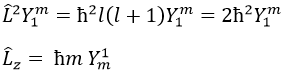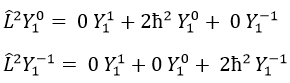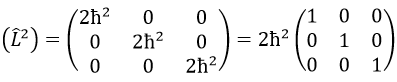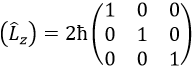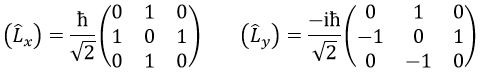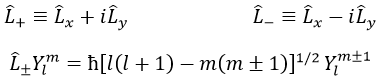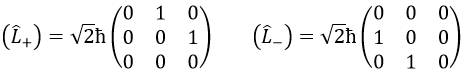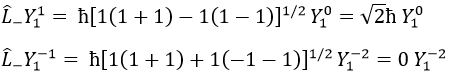Chapitre 10 : chimie physique moléculaire – opérateurs

Les opérateurs peuvent être appliqués aux fonctions d’onde et respecter l’équation de Schrödinger. L’inversion de l’opérateur Î est un opérateur tel que, si une symétrie centrale peut être trouvée,

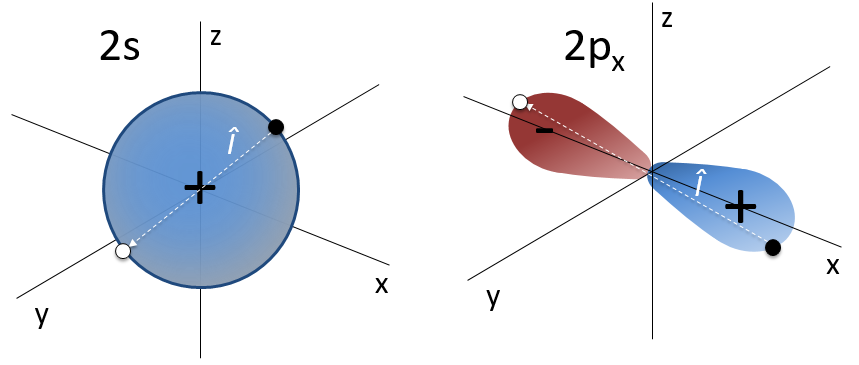
Par exemple, l’orbitale  s a un centre de symétrie. Nous disons que cet état est pair. Si nous appliquons l’opérateur d’inversion à cette orbitale, le signe de l’orbitale est toujours inchangé du côté opposé de l’atome (c’est-à-dire obtenu par symétrie centrale).

L’orbitale p est impaire parce que si nous regardons un point dans la partie positive de l’orbitale et appliquons la symétrie, nous serons dans le lobe négatif de l’orbitale. Les orbitales d sont paires. En fait, nous avons

L’opérateur Î peut également être appliqué aux électrons pour obtenir le spin opposé (en haut ou en bas).

Le moment angulaire L est le produit croisé de deux vecteurs r et p. Le produit croisé ou produit vectoriel est une opération binaire sur deux vecteurs et est désigné par le symbole ×. Étant donné deux vecteurs linéairement indépendants a et b, le produit croisé, a × b, est un vecteur c perpendiculaire aux deux et donc perpendiculaire au plan qui les contient (deux vecteurs linéaires partagent toujours un plan).

L’intensité du nouveau vecteur est a × b = |a||b| sin n (avec n le vecteur d’unité pointant dans la bonne direction) et la direction du produit croisé est donnée par la règle de la main droite: l’index se tient dans la direction du premier vecteur et le majeur dans la direction du second vecteur. Si vous placez votre pouce perpendiculairement aux deux autres doigts (pour montrer votre approbation), il indique la direction du produit croisé. Il peut être nécessaire de faire tourner votre main étrangement pour obtenir les bonnes directions, par exemple pour obtenir le b x un produit d’en haut.

En mécanique quantique, p est un opérateur

Nous avons donc

Notez que L_z ne dépend pas de Θ et  il y a donc une symétrie autour de l’axe Z pour cet opérateur. Si on applique l’opérateur L_z à la fonction d’onde angulaire, on obtient la fonction d’onde multipliée par ћm:

Cela signifie que la fonction d’onde angulaire est la fonction propre de l’opérateur Lz. C’est aussi le cas avec l’opérateur L².

Nous pouvons donc déterminer les  valeurs propres de L² simultanéments(=ћ²l(l+1)), charactéristique du moment angulaire L, et de L_z (=ћm), la projection de L sur l’axe z, pour valeurs fixes des nombres quantique.

La valeur propre d’un opérateur est l’intégrale de la fonction d’onde multiplié par l’opérateur agissant sur la fonction d’onde :

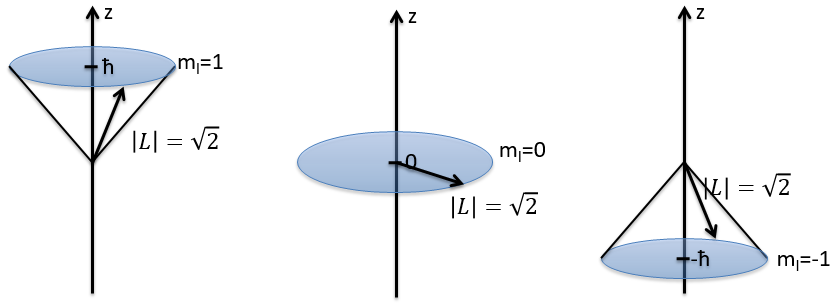
Et la longueur du vecteur L et de ses projections sur les axes :

Par exemple, pour l = 1, on peut dessiner L et sa projection en fonction de m. La longueur de L ne dépend pas de m.

L² et L_z commute: deux opérateurs qui ont la même fonction d’onde. La commutativité signifie que :

C’est en effet le cas : [L²,L_z]=0 et ce n’est pas le cas entre L_x, L_y et L_z:

Notez que L_x et L_y aussi commute avec L², comme L_z fait, mais leur valeur propre  <L_x> et <L_y> est égale à zéro.

Le même type de propriétés est vrai pour le spin des électrons avec les opérateurs S² et S_x, S_y, S_z.

Pour décrire l’ensemble du système, nous avons des séries d’équationscontenant les 5 nombres quantiques n, l, ml, s et m_s. Ils forment un CSCO(complete set of commuting observables) .

Représentation matricielle :

Dans une base orthonormée de fonctions {Ψ₁, Ψ₂,…Ψ_N}, l’opérateur  a une représentation matriciellethe (Â) qui est une matrice composée des opérateurs  Â_ij come.

si Ψ₁=Ψ₂, le résultat aurait été la bonne valeur de Ψ₁ si Ψ₁  est une fonction propre de Â. En générale on utilise la notation bra-ket de Dirac:

La partie avant l’opérateur est appelée bra et la partie après l’opérateur est le ket.

si Ψ₁  n’est pas une fonction propre de  (ÂΨ≠aΨ), alors nous pouvons trouver une combinaison linéaire (combili) de fonctions d’onde telles que :

ou écrit en tant que matrices

Prenons un exemple avec les opérateurs L_z and L² et les fonctions angulaires Y_m^l que nous avons utilisées auparavant pour l=1. La base complète des fonctions est Y₁^m={Y₁¹, Y₁⁰, Y₁^-1}. Les équations sont:

 Les valeurs de aij peuvent facilement être trouvées

L’équation pour Y₁¹ ne dépend pas de Y₁^-1 ou Y₁⁰. En conséquence, aij=0 for i≠j et aii=2ћ².

La même chose vaut pour Y₀¹  et Y₁¹

Ensuite, nous avons que la représentation de la matrice (L²) de l’opérateur L²

Cette matrice est diagonale, c’est-à-dire que les composants de la matrice qui ne sont pas sur la diagonale sont tous égaux à zéro. (L_z) est aussi diagonale.

La règle est que si les opérateurs sont des opérateurs de fonctions qui sont des fonctions propres à cet opérateur, alors la matrice est diagonale. Tous les opérateurs de la CSCO ont une représentation matricielle diagonale sur la base de leurs fonctions propres communes. Notez que cela signifie que Lx et Ly ne font pas partie du CSCO: ils ne commutent pas avec Lz et leur représentation matricielle est

C’est une conséquence directe du principe d’incertitude de Heisenberg: nous ne pouvons pas connaître la position exacte et la vitesse d’une particule en même temps. Par conséquent , L²  ne peut pas commuter avec tous les L_x, L_y et L_z.

On peut définir les opérateurs d’escalade L₊ et de descent L_– de L_x et L_y.

Pour notre exemple avec l = 1, ils sont :

Leur rôle est de passer d’une orbite à l’autre.

 

Comme le montre la dernière ligne, il est impossible de sortir du système. Il n’y a pas d’orbitale Y₁^-2.