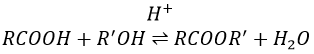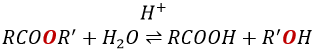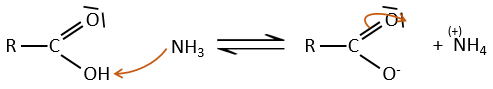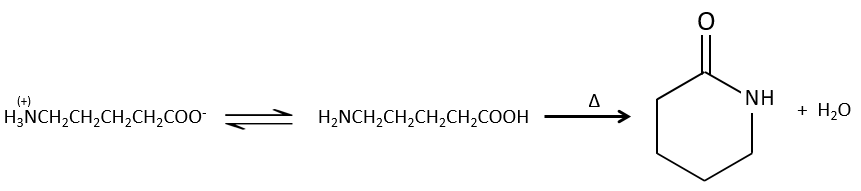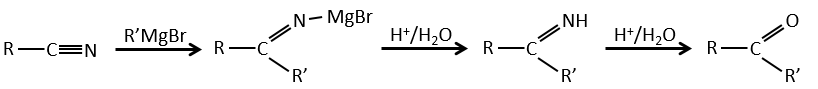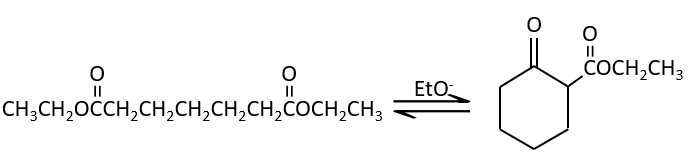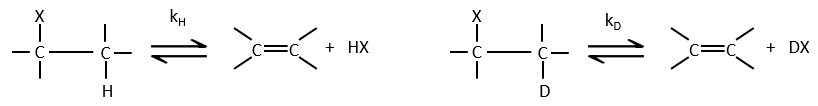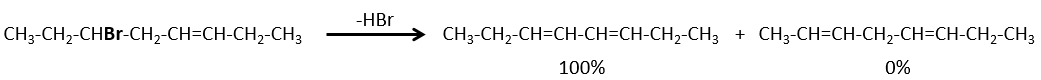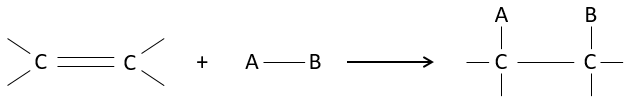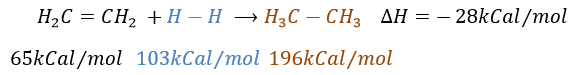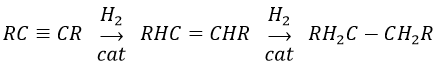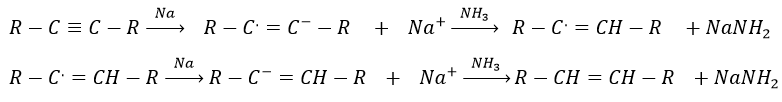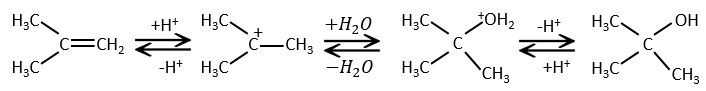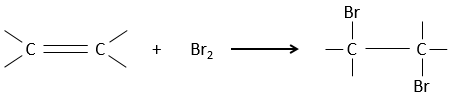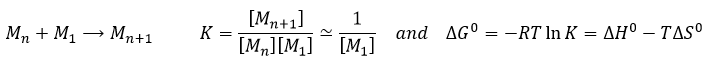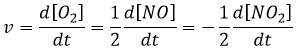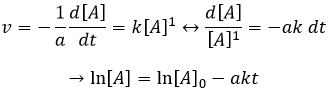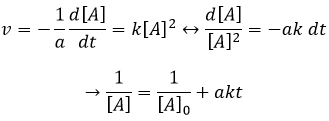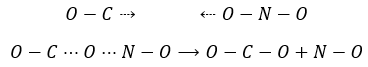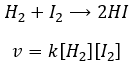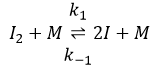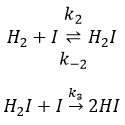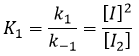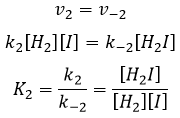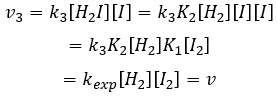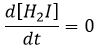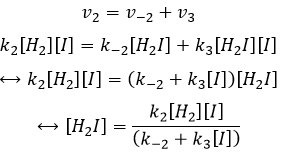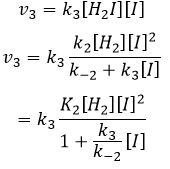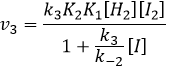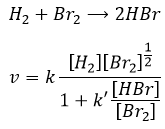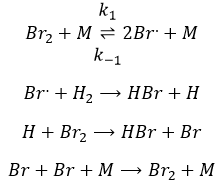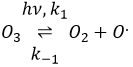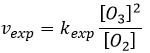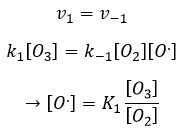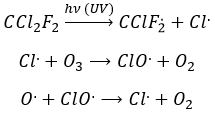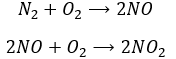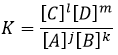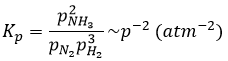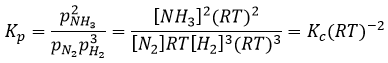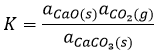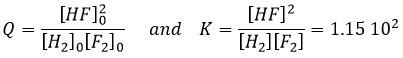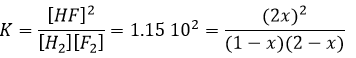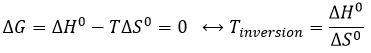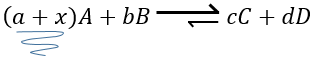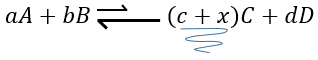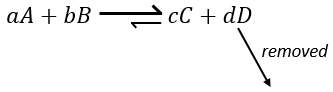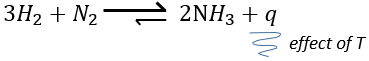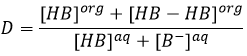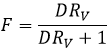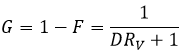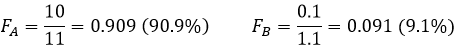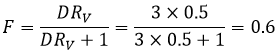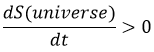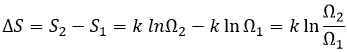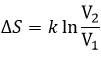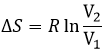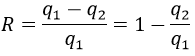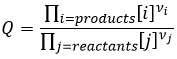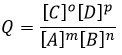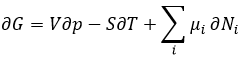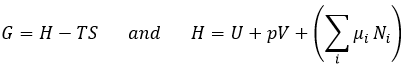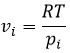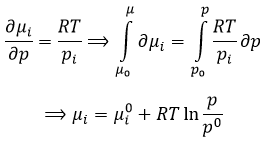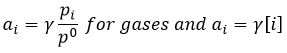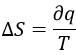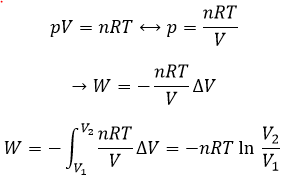Chapter 10 : Reactions of carboxylic acids and their derivatives
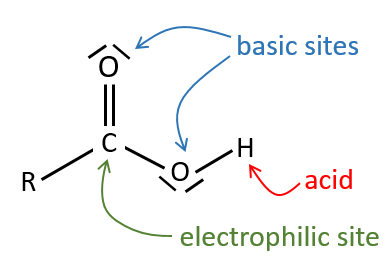
All the atoms of carboxylic acids groups have a specific character. The group is thus ambident: it possesses two or more alternative and strongly interacting distinguishable reactive centres. It has acidic and basic properties.
A carboxylic acid is more acid than the corresponding alcohol because the conjugated base, the carboxylate, is stabilised by resonance (pKa≈5 vs pKa≈17).
The oxygen of the carbonyl is more basic than the other one because the positive charge is more stabilised.
Synthesis of carboxylic acids
There are several ways to form carboxylic acids:
- by oxidation:
Carboxylic acids can be made by the oxidation of aldehydes or of alcohols. We can use CrO3 or KMnO4 as oxidants for instance.
- by Grignard

A reactant of Grignard can react with CO2 and then with water to form a carboxylic acid
- from nitriles

In acid environments, nitriles react with water to generate new acids and free a molecule of ammoniac.

This method can be used to extend a carbonic chain. Once a carboxylic acid is obtained, we reduce it to obtain an alcohol. The –OH group is removed by nucleophilic substitution and the whole loop restarts. Each loop adds one carbon to the chain.
The derivatives of carboxylic acids are
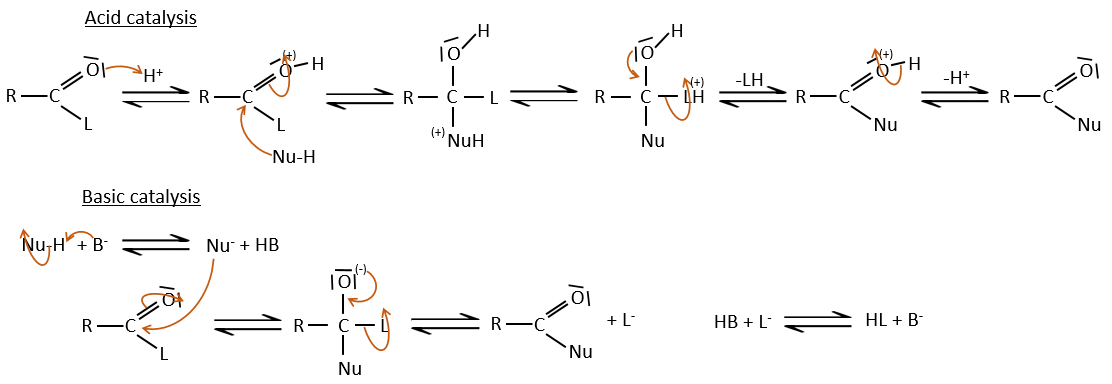
Reaction of Addition-Elimination
Carboxylic acids and their derivatives are attacked by nucleophiles on the carbon, as it is done for ketones and aldehydes. However, this addition is followed by an elimination.
It is thus the substitution of one group by the nucleophile at the condition that the group L that was previously on the carbonyl is a better leaving group than the nucleophile.
Cl–>RCOO–>RO–>OH–>NR2–>C–
As for ketones and aldehydes, the reaction can be catalysed by an acid or a base.
Note that the addition-elimination reaction for carboxylic acids is in competition with acid-base reactions. OH– is not a very good leaving group and if the nucleophile is a strong base, the carboxylate is formed. In the case of a nucleophile which is not a good base, there is a competition between the AE and the AB reactions.
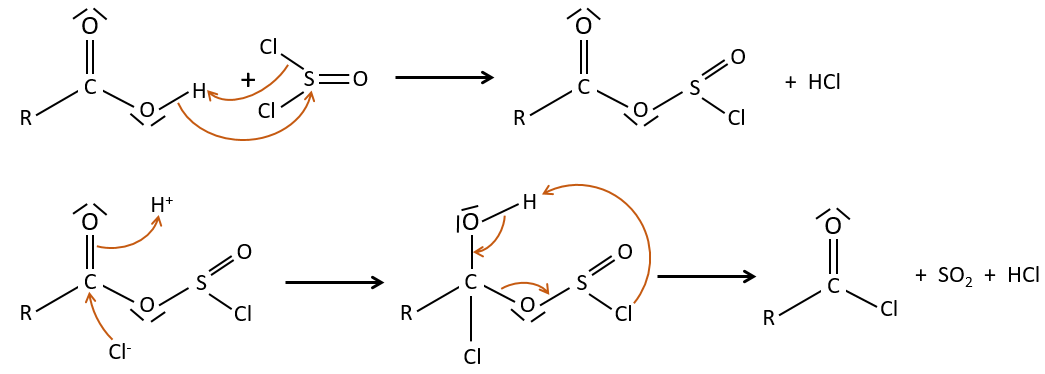
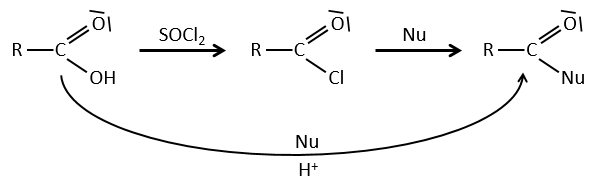
Formation of the acyl chloride
From what we wrote just above, we cannot replace RCOOH by RCOCl because Cl– is a better leaving group than OH–. However, there is a trick to make this reaction possible: we use thionyl chloride (SOCl2). The oxygen bound to the hydrogen in COOH is a nucleophile and can attack the sulphur atom, expelling a chlorine that catches the proton on its way. The newly formed chlorydric acid can now react with the thioester, eliminating a molecule of SO2 and of HCl.
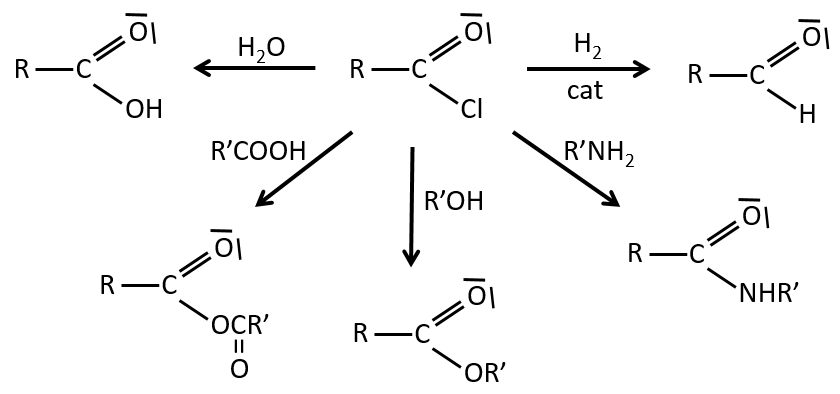
The same kind of mechanism is used to produce acid bromine from carboxylic acids and PBr3 (phosphorous tribromide). Yet, those reactions don’t work with HCOOH because the products HCOCl and HCOBr are unstable. They decompose in carbon monoxide and the corresponding acid.
Formation of esters
Carboxylic acids react with alcohols to produce esters.
Strong acids catalyse this reaction.
RO– is a slightly better leaving group than OH– so we want to displace the equilibrium towards the right by the use of an excess of alcohol or carboxylic acid and by the removal of water from the system. If we want to do the hydrolysis of an ester, i.e. the reverse reaction, we use an excess of water. It was shown that the hydrolysis of esters works this way (attack of the water on the carbonyl and not an attack of the water on R’) by the use of isotopes for the esteric oxygen.
Another way to obtain esters is the use of diazomethane, reaction that we have seen at the beginning of the elimination chapter.
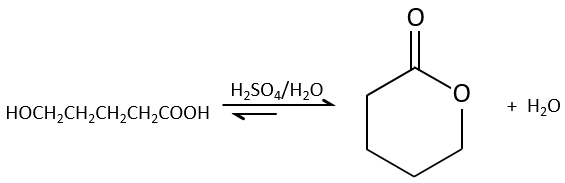
Intramolecular esterifications are more favourable than intermolecular ones for entropic reasons and are especially favourable if a cycle of 5 or 6 atoms is formed.
This kind of cycle is called a lactone (δ-lactone if a cycle of 6 atoms, γ-lactone if a cycle of 5, etc.). Lactones are sensible to the hydrolysis.
Formation of amides
Under normal conditions, an amine reacts with a carboxylic acid to form a salt (ammonium carboxylate) through an acid-base reaction. Once the amine has taken the proton, it cannot attack the carbonyl anymore.
If we heat up the system, the reaction goes back and another process, thermodynamically more favourable occurs, leading to the formation of an amide. In an amide, the nitrogen is not basic.
Intramolecular reactions are possible and lead to the formation of lactams.
Reactions of carboxylic acids and their derivatives
We have shown several reactions of the carboxylic acids. It is often interesting to consider to transform the carboxylic acid into an acyl chloride prior to the desired reaction. Acyl chloride are usually more reactive and this additional step in the process can increase the global yield of the reaction.
Reactions of acyl chlorides
From the acyl chloride, we can obtain many other functional groups.
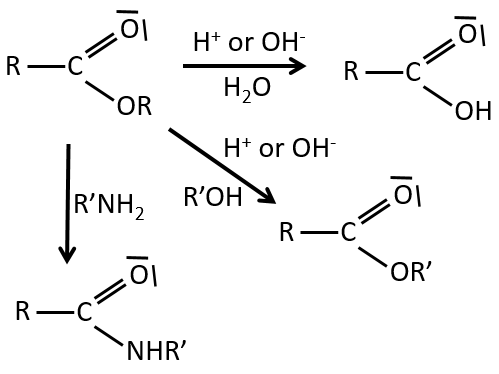
Reactions of esters
As ester are less reactive than the acyl chlorides, less reactions are available. We can hydrolyse the ester, exchange the esteric chain with another one or generate an amide.
An additional reaction is to use a Grignard reactant on an ester to obtain a tertiary alcohol. The ketone is more reactive than the ester so the reaction continues.
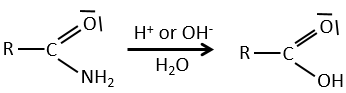
Reactions of amides
Peptide bonds can be hydrolysed.
Reactions of nitriles
The carbon atom from a nitrile is at the same oxidation state than the one of the carboxylic acid. A nitrile in presence of water and acid leads to the formation of a carboxylic acid and the rejection of ammoniac.
Nitriles can also react with reactants of Grignard but the reaction stops at the formation of ketones.
Nitriles can also be reduced into primary amines by LiAlH4.
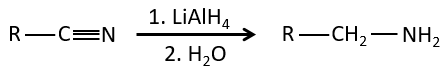
Chapter 9 : carbanions in α of carbonyl
In the previous section, we discussed the possible reaction on the carbonyl group of organic molecules. The carbon is an electrophile and the oxygen is a nucleophile. Yet, the presence of a carbonyl can imply other processes. The hydrogen’s that are on a carbon neighbour of a carbonyl group, i.e. the carbon in α of carbonyl, are acid and strong bases can snatch it.
Its pKa is around 20 (for comparison, the hydrogen of a –C-H has a pKa of 40, a =C-H a pKa of 37 and –O-H a pKa of 18). The result is the enolate ion. It is stabilised by resonance with the carbonyl.
Tautomerization
The enolate ion can react by its oxygen or the carbon in α.
Enols are usually unstable and tautomerize into the corresponding carbonyl. It is the enol-ketone tautomerism. The tautomerization is done by acidic or basic catalyse.
The difference of energy is about ΔG=15kcal in favour or the ketone form. The enol-ketone equilibrium can be displaced if one form is stabilised by the structure of the molecule.
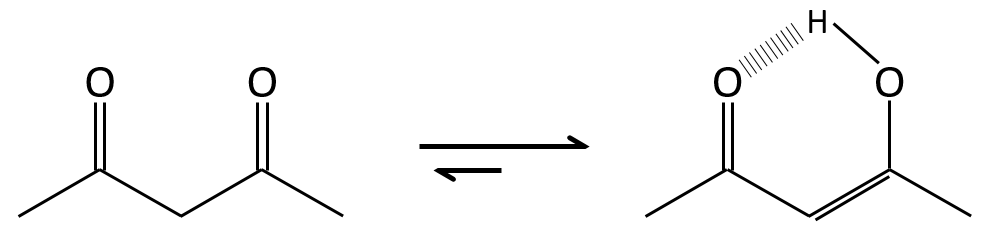
The tautomerization allows to modify the conformation of the molecule. A cis molecule tautomerizes to become trans and decrease the steric hindrance.
We can also exchange hydrogen’s for its isotopes because of the tautomerism.
The chemical properties of isotopes are almost identical (because given by the electrons), but some physical properties can be different between isotopes of the same element. The speed of reaction and the ebullition temperature are two examples of properties that change depending of the isotope. It is thus possible to separate the species wearing isotopes by distillation or by centrifugation.
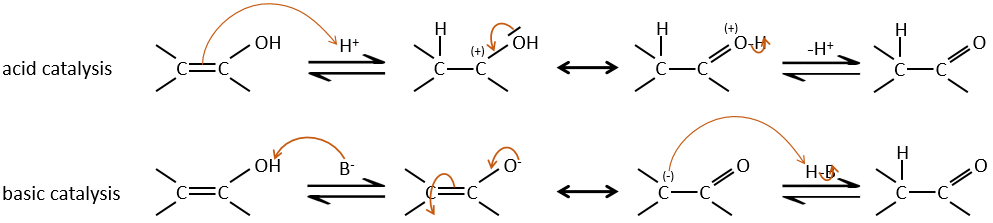
Halogenation
The hydrogen can also be exchanged with halogens through acidic or basic catalyse. In this case, the results are different depending on which catalyst we use.
– Acid catalysis:
Once one halogen is on the molecule, it is harder to form the enol because it is more difficult for C=O to catch a proton due to the inductive captor effect of the halogen.
– Basic catalysis:
During the basic catalyse, we don’t have to protonate the carbonyl and the halogenation can take place as many times as there are α protons.
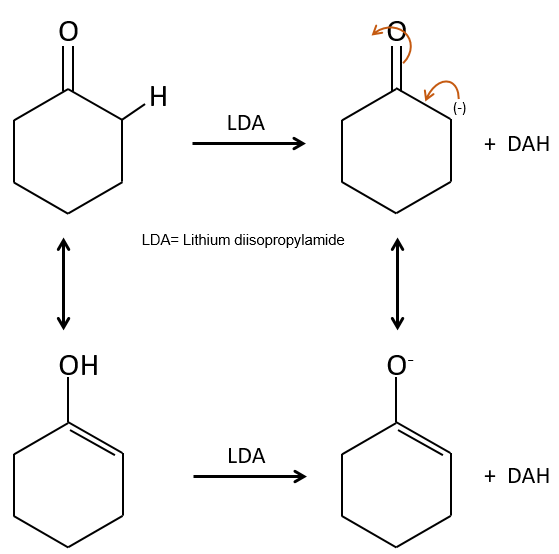
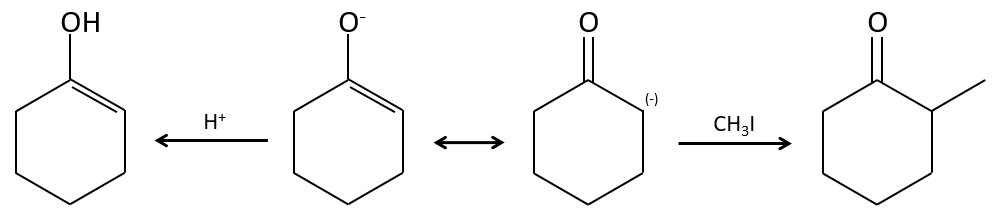
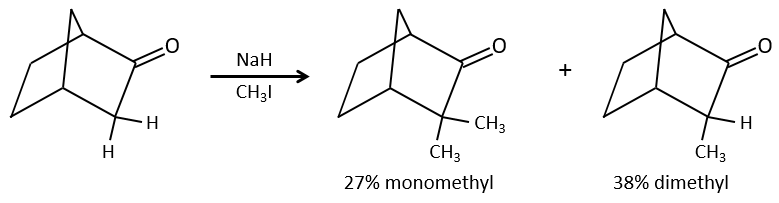
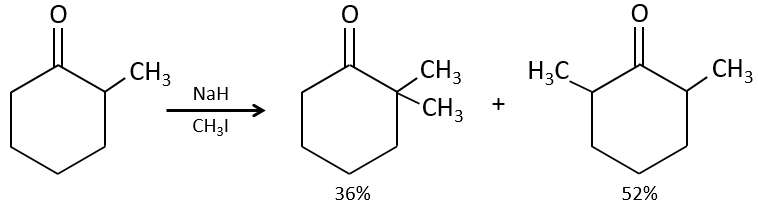
Alkylation
We have seen in the previous section that NaH alone doesn’t reduce carbonyls. However it has an effect on the carbon in α of carbonyls. It is a good way to introduce an alkyl group at this position.
A strong base can also take the proton α of carbonyl.
One problem is that the reaction can continue if there are several hydrogen’s in α of carbonyl and polyalkylation is frequent, leading to a racemic mix of products.
Moreover, the regioselectivity is low, giving an additional possibility of product.
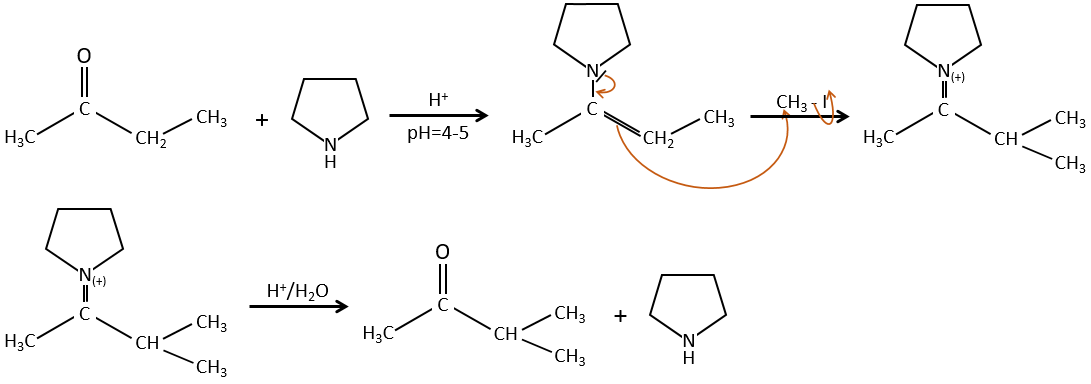
To avoid polyalkylation, we can replace the oxygen by pyrrolidine (C4H9N) to obtain the corresponding enamine that has the advantage of a low polyalkylation.
This protection is also effective for aldehydes that are subject to the aldol condensation reaction in basic environments.
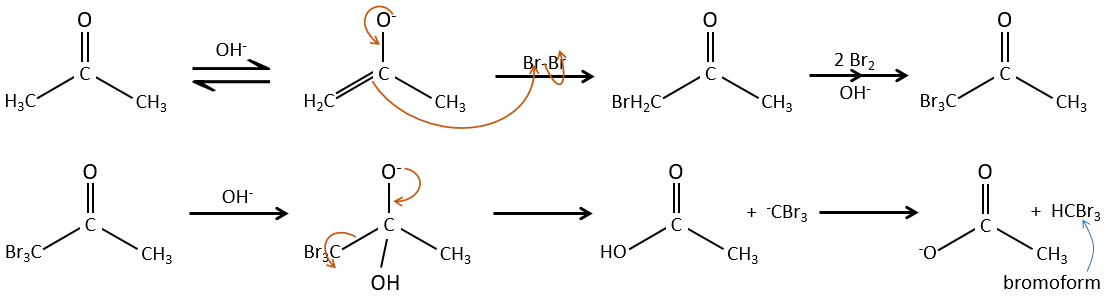
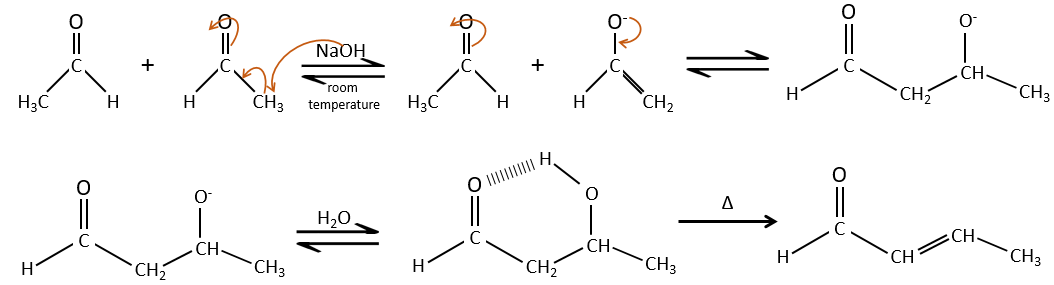
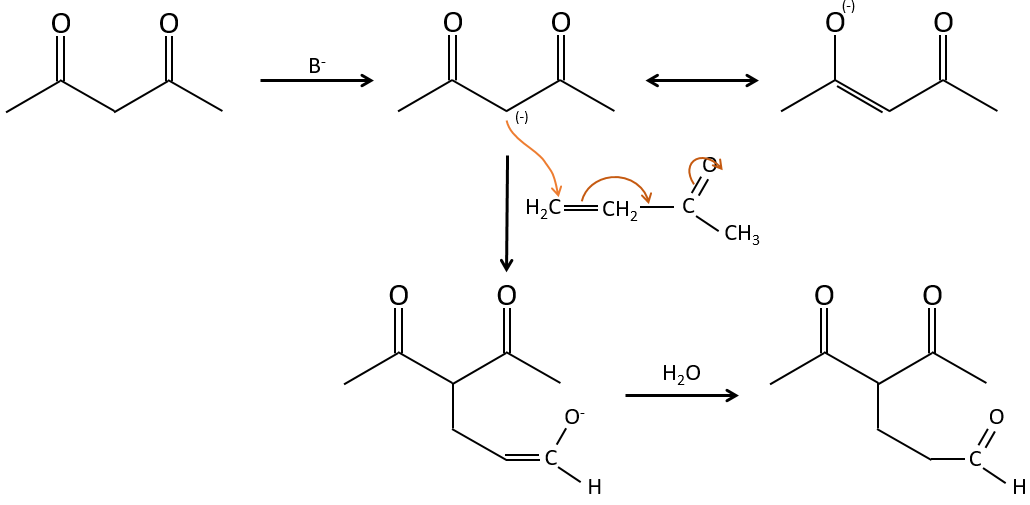
Aldol condensation
If we add a few NaOH in a solution of acetaldehyde, dimers are formed. The first step is the deprotonation in α of carbonyl by the base to obtain the enolate ion that attacks next another aldehyde, leading to the formation of a β-hydroxyaldehyde. The β-hydroxyaldehyde is stabilised by its internal hydrogen bond.
If we heat up the solution, the molecule loses a water molecule to form an enone (double liaison conjugated with a carbonyl).
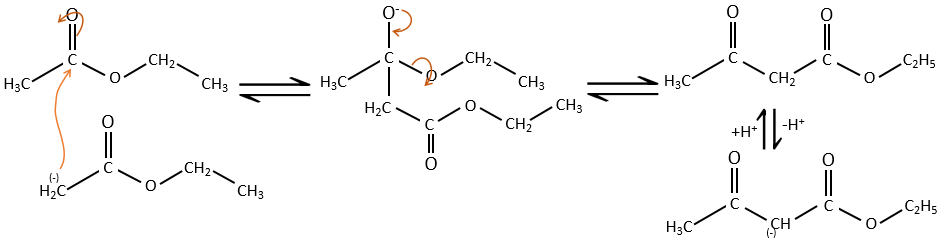
Condensation of Claisen
The analogue reaction for esters is called the condensation of Claisen. NaOH is not used in the present case because it would cleave the ester. We can use sodium ethoxide instead for instance to obtain the enolate ion.
As for the aldol condensation, the enolate ion attacks another ester to obtain β-ketoesters.
The condensation of Claisen can be made with two different esters (mixt condensation of Claisen) or between two esters in the same molecule (intramolecular condensation of Claisen).
The intramolecular reaction is favoured in comparison to the intermolecular one because it does not decrease the entropy.
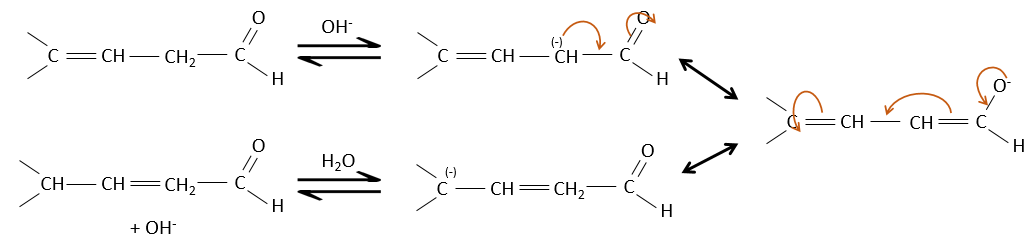
Properties of α,β unsaturated aldehydes and ketones
Such species are stabilised by resonance.
They are way more stable than β,γ-unsaturated aldehydes/ketones that rearrange themselves into the α,β unsaturated compound in presence of a base.
Obviously, the double liaison and the carbonyl groups can go through reactions independently, such as addition reactions for example.
But additions can also be made in several cases on the conjugated system. Those are 1,4 additions.
The nucleophilic attack is possible on the carbon of the double liaison because it is depleted by the conjugation with the carbonyl.
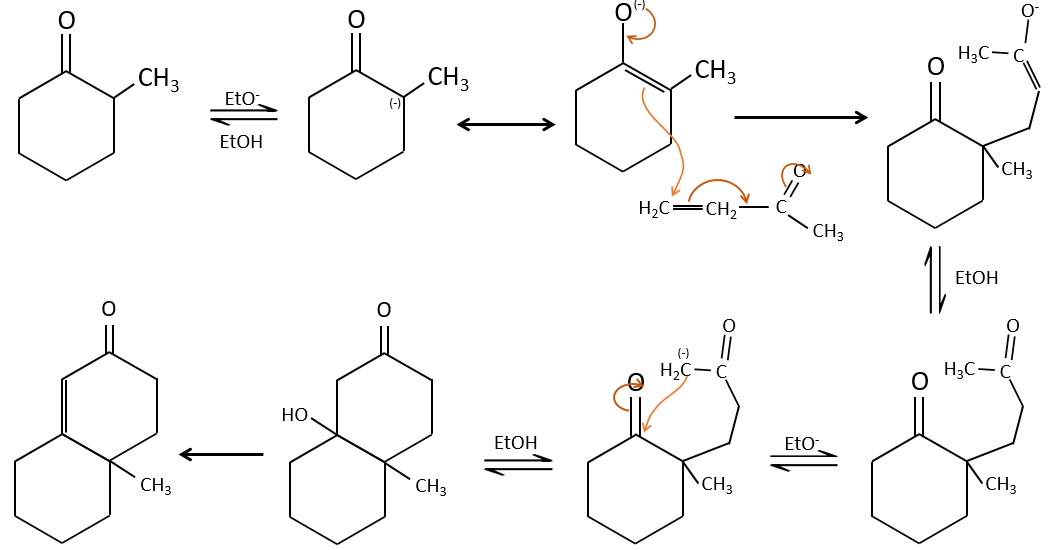
The Michael’s addition is the 1,4 addition of an enolate ion on an enone:
A Michael’s addition can be followed by an intramolecular aldol condensation, the reaction is known as the annulation of Robinson.
Chapter 8 : Reactions of elimination
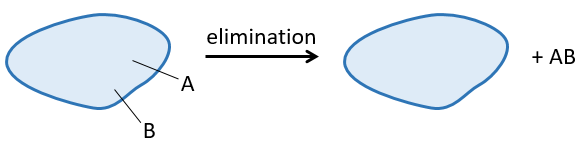
A reaction of elimination is a reaction during which one molecule loses two fragments A and B as a neutral substrate AB.
The two fragments A and B that are removed can be removed from the same carbon, in which case we talk about a 1,1 elimination, from two adjacent carbons (1,2 elimination or beta elimination) or two carbons separated by one carbon (1,3 elimination). The 1,2 elimination is the most common one.
Elimination 1,1
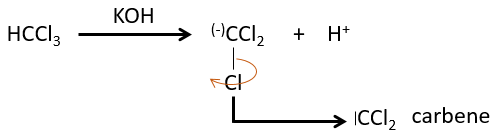
The two fragments are removed from one single carbon. It leads to the formation of a higly reactive carbene.
This reaction is possible because the chlorine atoms take the electrons from the carbon. Because of that, the C-H bond is destabilised and a strong base can remove the proton.
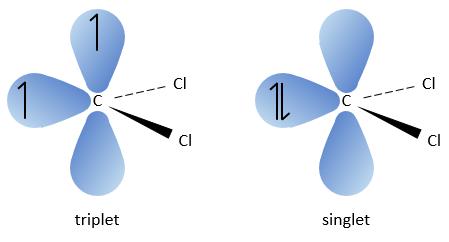
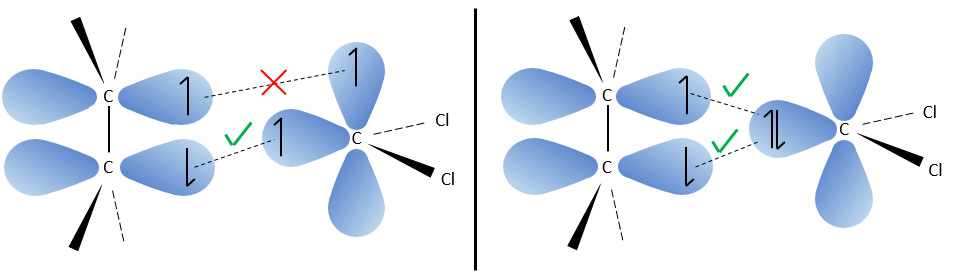
The carbon of the carbene is a singlet and is less stable than a triplet. It will thus react quickly with double liaisons to obtain a cyclopropane chain. A triplet would not be able to attack the π liaison.
The reaction is stereoselective (on the same side of the plane).
The smallest carbene is the methylene that can be produced from diazomethane (check nom anglais). The diazomethane is toxic and explosive so the reaction has to be controlled.
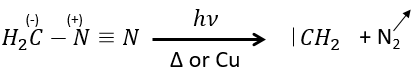
It can also be used to produce methyl esters.
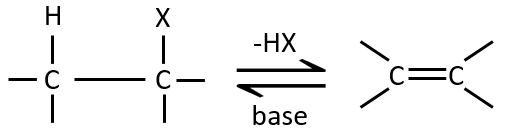
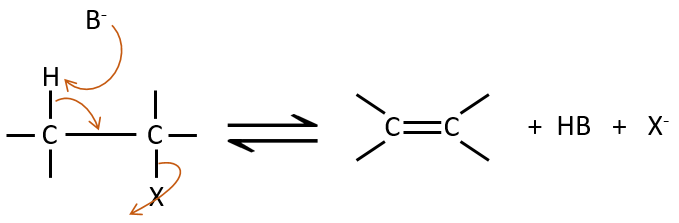
Elimination 1,2
This kind of elimination leads to the formation of new π liaisons. It is the opposite of a reaction of addition. We will only discuss the main reaction of β elimination but there can be other mechanisms involved to obtain such a reaction.
Similarly to the substitutions, where there is a mechanism with a kinetic of order 1 (SN1) and one of order 2 (SN2), there is an elimination of order 1 (E1) and of order 2 (E2).
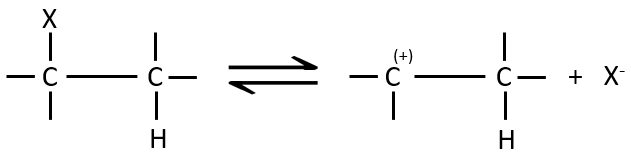
E1 mechanism
The first step of the reaction is the departure of one anion and the formation of a carbocation. This step is slow and is determining the speed of the reaction.
The second step is the capture of a proton on the adjacent carbon by a base. It leads to the formation of the π liaison to have a neutral species.
We can know if an elimination is of order 1 from
- the order of the kinetic of reaction (order 1).
- the isotopic effect: if the hydrogen is replaced by a deuterium, we don’t see any modification of the speed of reaction. It is so because the hydrogen doesn’t take part in the determining step. If it was involved, the speed would be divided by 5 to 8.
- the stability of the carbocation: the stability of the carbocation (degree of substitution or hyperconjugaison) affects the speed of reaction.
- rearrangements: explained by the existence of a carbocation.
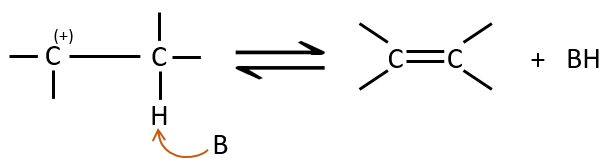
E2 mechanism
The kinetics is of order 2 and involves a reaction in one step, where the base takes the proton and the departure of the leaving group are simultaneous.
This reaction is only made if the proton and the leaving group are in anti positions.
The argument in favour of the E2 mechanism are
- a kinetic of order 2
- a huge isotopic effect
- no rearranging
- huge influence of the energy of the C-X bond (X– is the leaving group)
Competition between the mechanisms
As for the nucleophilic substitutions, there is a competition between the two mechanisms. It is not always 100% of E1 but it can be a mix of both, eventually leading to a racemic melange of products. The strength of the base and the steric hindrance influence which elimination mechanism is used: a strong base favours the E2 mechanism while a weak base and steric hindrance favours the E1 mechanism.
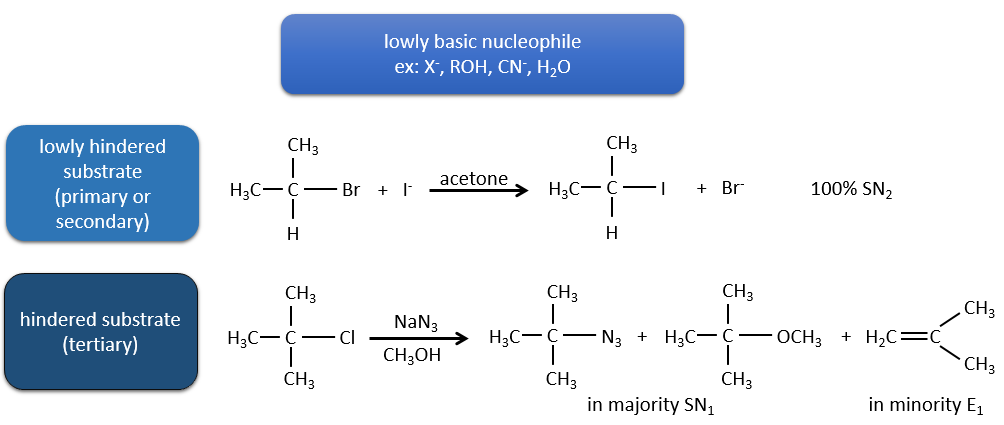
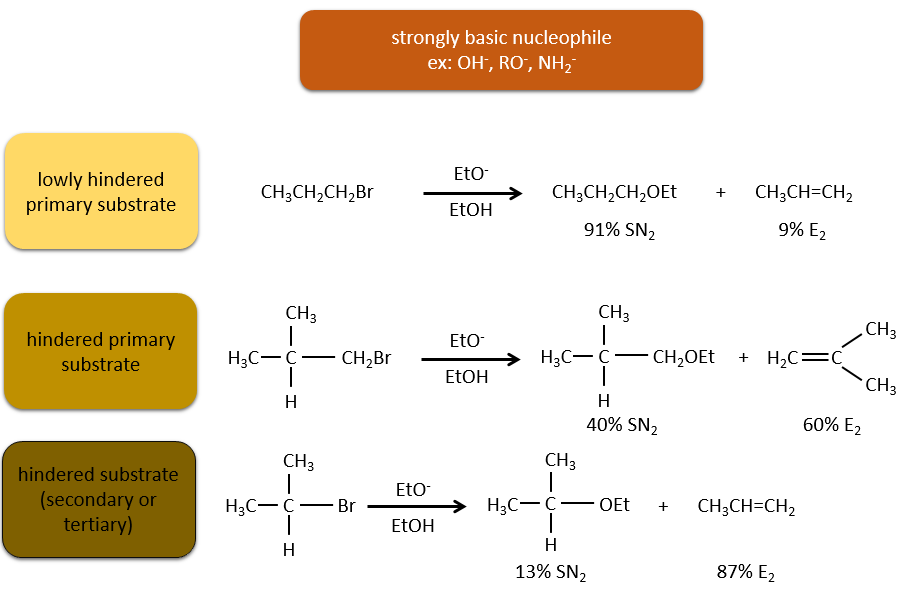
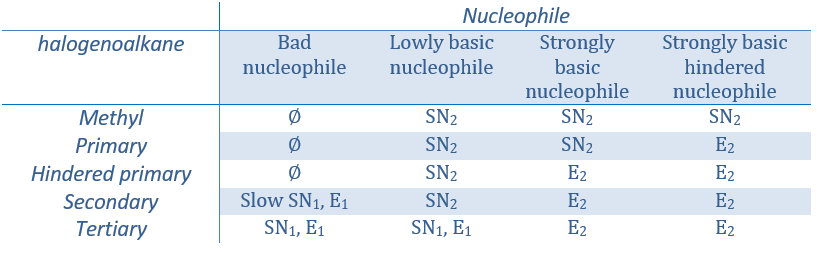
Now, the molecules with a good leaving group can often also be the target of a substitution reaction in presence of nucleophiles. There is thus a competition between E1, E2, SN1, SN2 and eventually other reactions. The three main parameters to consider to determine which reactions should occur are the strength of the base, its nucleophilicity and the steric hindrance.
Nucleophiles that are bad nucleophiles have good yields with SN2 with primary and secondary substrates. If the steric hindrance is larger, the main product becomes the SN1 product. If the nucleophile is a strong base, the main product is the SN2 but if the steric hindrance increases, the elimination becomes more important.
Nucleophiles that are strong bases and that are hindered favour the elimination.
To resume:
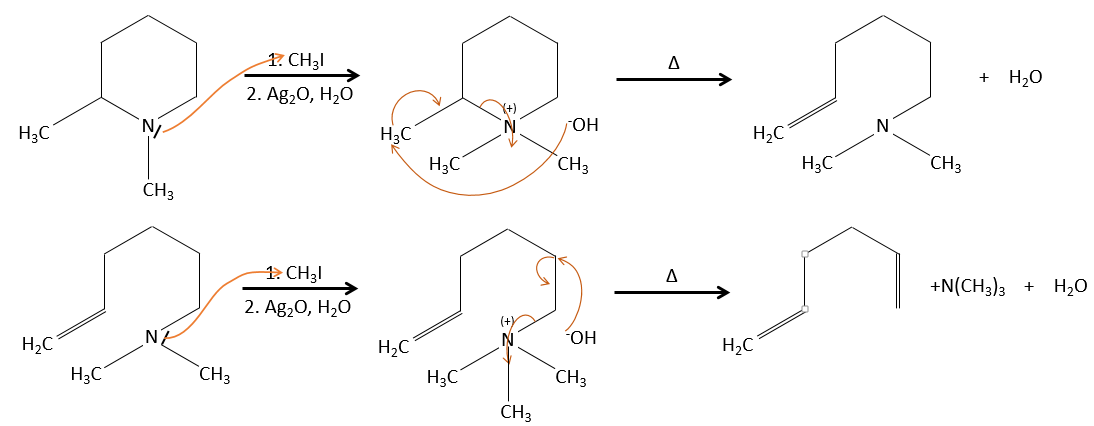
Regiochemistry of the elimination
When the carbon wearing the leaving group is not at one extremity of a chain, there can be several possible products. We can predict which hydrogen will be removed.
- If the generated double liaison can be conjugated with other π liaisons, those products will be favoured.
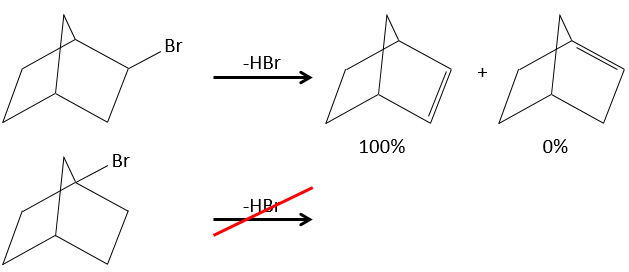
- In the case of bridged substrates, the product never involves a π liaison on a bridgehead carbon.
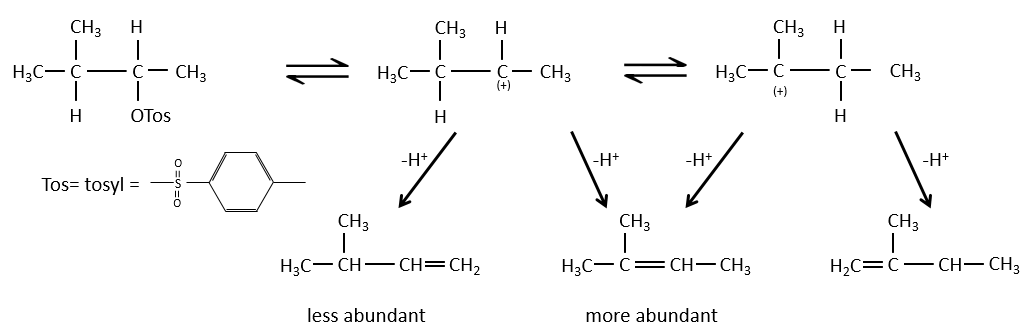
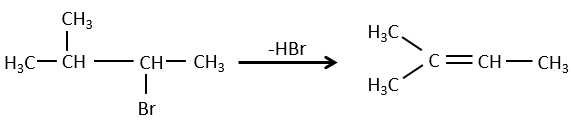
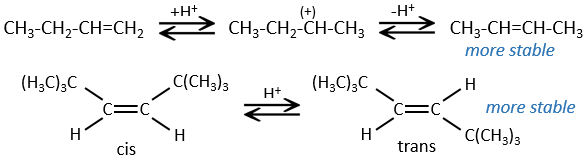
- For E1 eliminations: the elimination is determined by the stability of the formed olefins. The most substituted C=C is thus favoured. It is the rule of Zaitsev.
– There can be exceptions because of steric hindrance
- for E2 eliminations, one H in anti is required
- the rule of Zaitsev is followed if the leaving group is not charged (most substituted C=C)
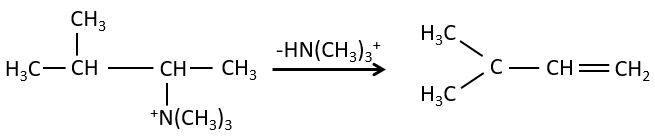
- it is the opposite it the leaving group is charged: it is the rule of Hofmann
Configuration of the product
In the case of one E2 elimination, the reaction is stereospecific and there is thus only one possible configuration.
In the case of one E1 elimination, the product is more stable if the voluminous substituents are in trans.
Dehydratation of alcohols
This elimination does not occur in basic or neutral environments: OH– is a bad leaving group and we would form –O– in presence of a strong base.
In an acidic environment, the elimination can be done by E1 or by E2. The E1 is favoured in the case of substituted products and the E2 is the main mechanism for primary carbons.
Reactivity: tertiary>secondary> primary
E1 E1 E2
Fragmentation of 1,3 diols
It is one case of 1,3 elimination during which the molecule is cleaved
Chapter 7 : Electrophile additions on alkenes and alkynes
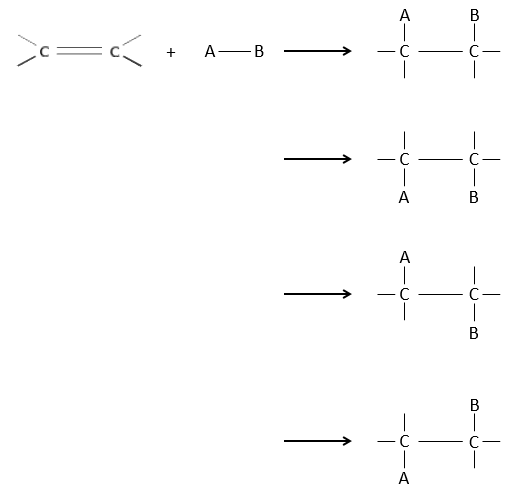
The interest of electrophile additions on C=C liaisons is to transform two sp2 carbons into two sp3 carbons and to add a chain or a group on the existing molecule.
As two carbons are involved in the reaction, the addition of the new group can give several products, with more or less (stereo)selectivity. Moreover, the transformation into sp3 carbons also introduces a regioselectivity that often has to be considered.
Consequently, we will discuss in this section the methods and the rules that have to be followed to obtain the desired product during the addition of an electrophile group on double or triple liaisons.
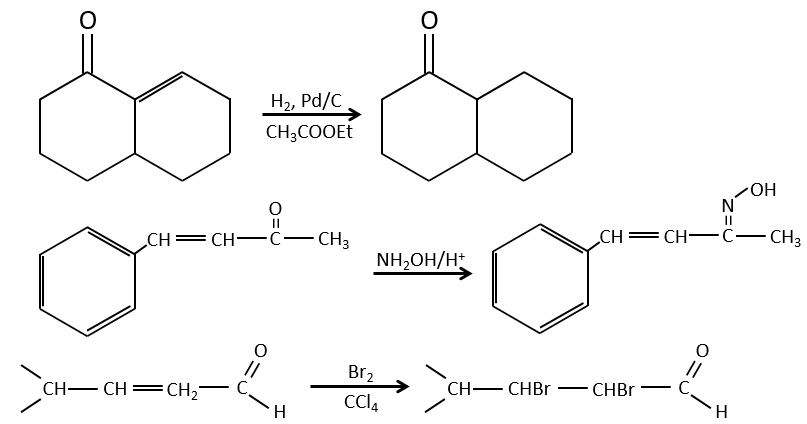
Catalytic hydrogenation
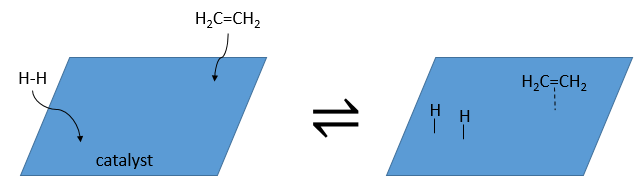
It is, in the principle, the easiest addition on a C=C liaison because there is no new group on the product. The sp2 carbons are reduced into sp3 carbons. Yet, this reaction is not spontaneous despite the fact that it is an exothermic reaction. The activation energy to break the H-H liaison is huge and a catalyst is required to perform the reaction.
As catalyst, we can use platinum (Pt), Raney’s Nickel (Ni) and Palladium on C (Pd/C).
The have the ability to dissociate the hydrogen atoms and to fix them on their surface, making them available for the addition on the alkene. As detailed in the kinetics section, the catalyst decreases the energy of activation of the reaction and the process can be depicted in 4 steps:
– approach and binding of the reactants
– displacement on the surface
– reaction(s)
– departure of the products
At the first step, the reactants take place on the surface of the heterogeneous catalyst. The amount of reactant that can take place on the catalyst depends on its surface. It is thus advised to use small particles of catalyst to increase the ratio surface/volume (or surface/mass). The alkene places itself parallel to the surface, in the direction of the π liaison.
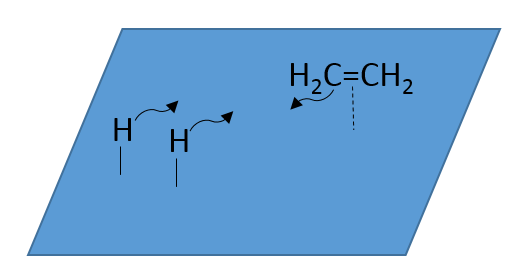
There is no reason that the reactants immediately bind on nearby spots. The second step is thus that the reactants are moving on the surface. They will eventually be in contact with each other so that the reaction can take place.
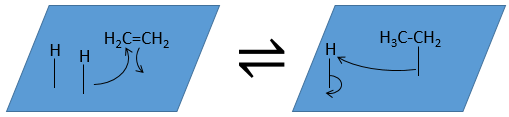
The third step (and eventually the next ones) is the reaction between the reactants. One activated hydrogen attacks one sp2 carbon while the π liaison is now connecting the second carbon with the platinum. The next step of the reaction is that the liaison between the carbon and the platinum attacks the remaining hydrogen.
As last step, the alkane leaves the surface of the catalyst, letting space for reactants to bind.
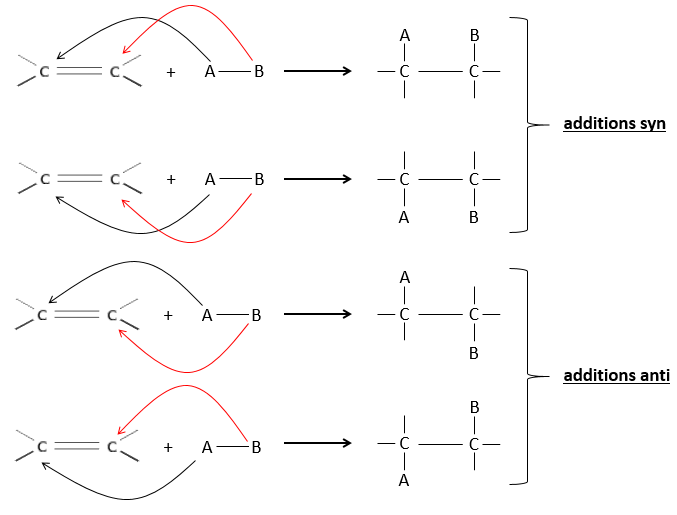
The hydrogenation is stereoselective, i.e. the place of the groups on the carbons are not equivalent: at the level of the C=C liaison, the molecule is planar. If the hydrogen atoms are fixed on the same side (but not on the same carbon) of the molecule. It is a syn addition. As the added groups are hydrogen’s, the product is thus cis (see nucleophilic substitutions about cis and trans products).
If the groups were added on the opposite sides of the molecules (still not on the same carbon), the addition would be anti and the product would be trans. This product is not observed because the reactants are bound to the catalyst and cannot move freely during the reaction. Both hydrogen’s are thus on the same side of the molecule before the reaction and after the reaction.
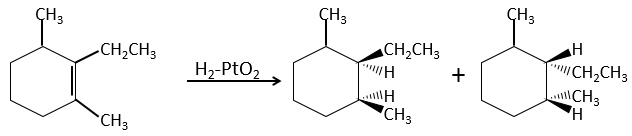
This is of importance only if, after the reaction, the newly sp3 carbon cannot rotate. It will be the case when the liaison is involved in a cycle or if there are voluminous groups. Moreover, the fact that we obtain only the cis product does not mean that only one product is possible. The reason is that there is one plane at each side of the π liaison (for a total of 2). If the two planes are equivalent, we will obtain a 50-50 racemic mix of two cis products.
If the planes are not equivalent, one product is favoured: the hydrogen’s are fixed on the least occupied side because the alkene places itself on the catalyst so that the voluminous groups are far from the catalyst.
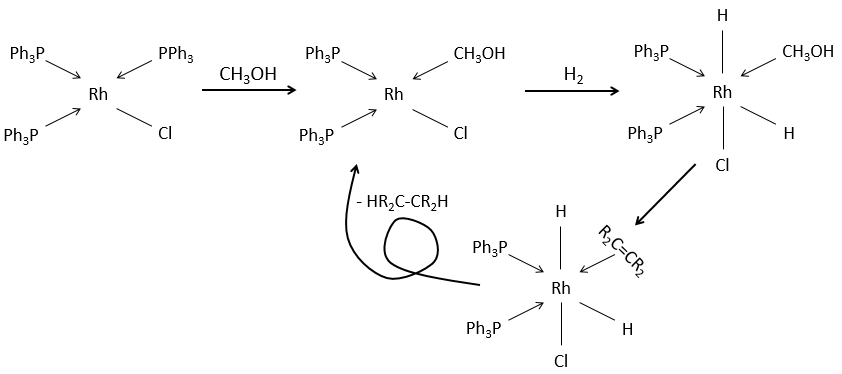
Soluble catalysts can also be used for this reaction. It is the case for the Wilkinson’s catalyst chloro(tris(triphenylphosphine)rhodium(I).
It also lead to the cis products.
In terms of reactivity, the substituted carbons react slower than carbons with less groups because of the steric hindrance: the hydrogen’s are not very mobile on the surface of the catalyst and the π liaison has to be nearby to obtain the hydrogenation.
The alkynes also react faster than alkenes, allowing us to hydrogenate all the alkynes into alkenes before the formation of alkanes. We can thus limit the hydrogenation to the alkenes if we use a bad catalyst and put one equivalent of H2 by alkyne. We will obtain the alkane with 2 equivalents of H2 by alkyne.
Again, it will lead to the cis alkene. To obtain the trans alkene, we use sodium in ammoniac. The sodium generates a radical on one carbon and a negative charge on the other one.
The trans product is favoured for steric reasons.
Aromatic products can difficultly be hydrogenated with H2/cat (at 150°C) but it can also be reduced differently by the reduction of Birch, involving Na, NH3 and an alcohol.
Other electrophile additions
Addition of HX
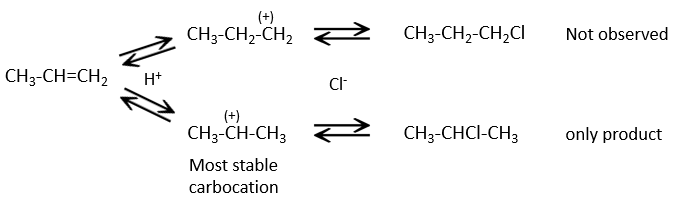
The other reactants HX containing a hydrogen atom can more easily be broken (or are already ionic) and do not require a catalyst. In the case of a halogen acid, because of their nucleophilic character, the π liaisons which are weaker than σ liaisons tend to attack electrophile molecules. In this case, the electrophile target is the proton. It is called an electrophile attack. The nucleophile X– attacks the positive carbon (or carbocation) afterwards.
This reaction does not involve stereoselectivity because there are two distinct steps but involves regioselectivity: it is the rule of Markovnikov that says that the halogen is fixed on the most substituted carbon, or inversely that the proton is fixed on the least substituted carbon. Personally, I prefer to remember that the most stable carbocation is formed. Remember that carbocations can rearrange the molecule to form the most stable carbocation.
Addition of water
Water is added to alkenes in presence of sulphuric acid.
The sulphuric acid is chosen because the sulphate is less nucleophilic than the water because the charge is stabilised by resonance. HCl has to be avoided because Cl– is more nucleophilic than H2O. Moreover, all the steps are reversible. It means that the newly generated alcohol can be dehydrated in the case of an excess of acid.
The presence of a carbocation explains some rearrangements of alkenes that can be observed in acidic solvents.
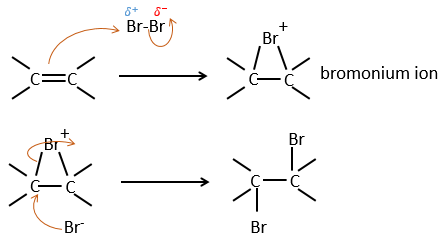
Addition of X2
Halogen’s are added to C=C to obtain trans products.
It is strange that something as charged in electrons as halogens are used as electrophiles for this reaction. The reason is that the liaison between the halogens is polarisable. A halogen will thus feel the electrons of the π liaison and transfer part of its electrons to the other one. The partially positive halogen can thus be attacked by the π liaison and forms an intermediate halonium that will be attacked by the negative halogen on the other side of the C-C liaison.
This reaction is stereoselective (always trans) and stereospecific (the result depends on the arrangement of the reactant). In presence of other nucleophiles, such as water, the reaction begins normally but there is a competition between X– and the nucleophile.
This reaction is slower on alkynes because the intermediate halonium is less stable. The halogenation is thus hard to control: the alkenes will react faster than the alkynes.
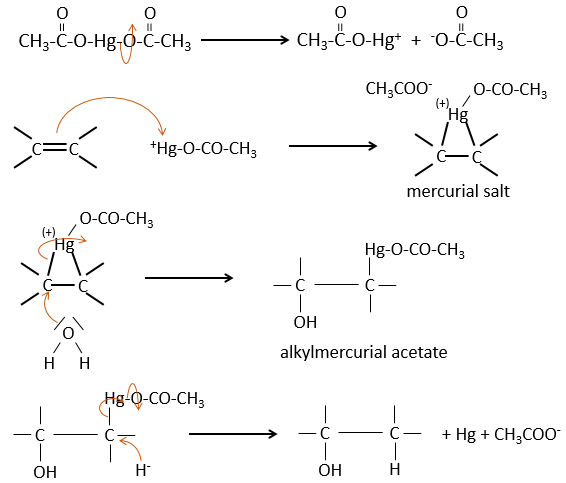
The oxymercuration reaction
This reaction is a useful way to form alcohols or ethers from alkenes. It involves mercurial acetate and water/alcohol in THF as solvent. The nucleophilic opening of the water/alcohol is done in anti and on the most substituted carbon (so there is more space for the mercurial acetate).
The oxymercuration follows the Markovnikov rule but there is no carbocation involved in the process. As all the additions, it is regioselective.
Water leads to the formation of an alcohol and we can use an alcohol instead of the water to obtain an ether.
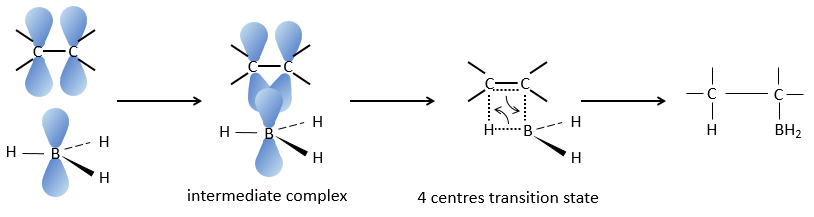
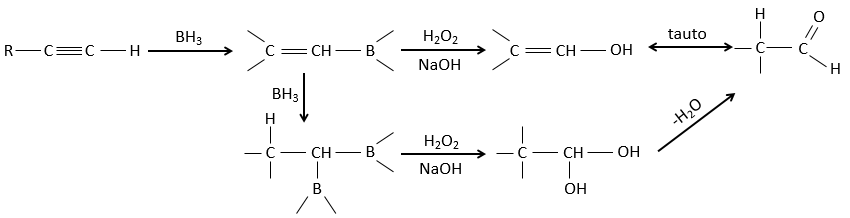
Hydroboration reaction
BH3 (borane) is a Lewis acid that is stable under the form of a dimer and can replace its 3 hydrogen by 3 carbon chains in THF (tetrahydrofuran (CH2)4O). Once the chains are bound, it is possible to remove the boron by an oxidation with H2O, NaOH and H2O2 to obtain as many alcohols.
This reaction does not follow the Markovnikov rule (anti-Markovnikov) and is stereoselective. The mechanism of reaction involves the empty p orbital of the boron that interacts with the π liaison to form a complex. This complex allows a transition state with 4 centres wherein the liaisons move.
The Markovnikov rule applies when the hydrogen is positively charged. In the present case, we add H– and BH2+.
The removal of the boron is made with retention of configuration and is stereospecific. The boron is less electronegative than the carbon and is thus giving its electrons. NaOH takes a proton from the H202 to form HOO– that attacks the boron, transferring its negative charge. There is a rearrangement occurring that puts an oxygen between the chain and the boron.
The water and OH– take action next to remove the boron.
This addition can also be done on alkynes to form aldehydes through tautomerization.
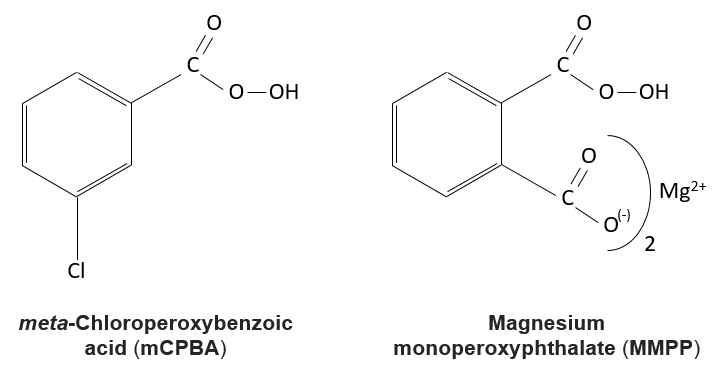
Reaction of alkenes with peroxycarboxylic acids
The peroxycarboxylic acids are generally unstable. The MCPBA and the MMPP are however stable peroxyacids vastly used in laboratory.
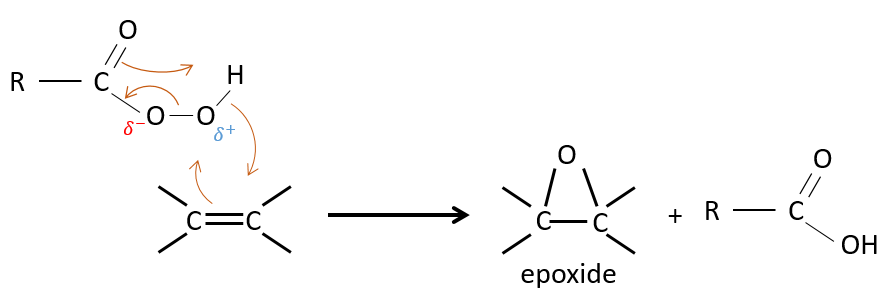
One of the oxygen of the peroxycarboxylic acids is electrophile. Those acids can thus react with alkenes to form epoxides and the carboxylic acid.
The addition is thus a concerted reaction, is stereospecific and is syn. The reaction is made on the less hindered plane of the alkene. The reactivity increases with the amount of substituents that share their electrons with the π liaison (alkyl chains for example).
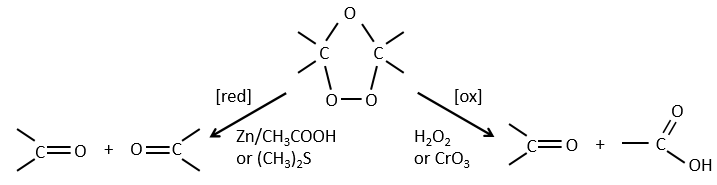
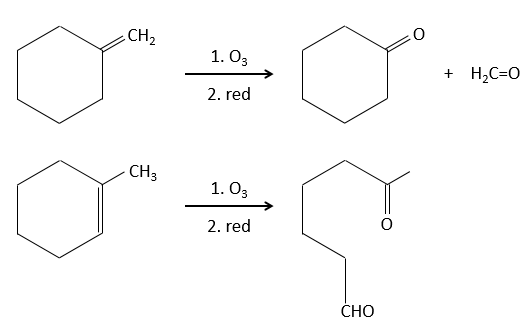
Ozonolyse
The ozone can break double liaisons. As a first step, it opens the double liaison to give the intermediate called molozonide.
It breaks to form ozonide that can next be oxidized or reduced.
The following table gives the products of the ozonolyse as a function of the substituents of the double liaison.
The ozonolyse is thus a good way to obtain ketones and carboxylic acids from alkenes. The method is also useful to determine to position of a double liaison in a molecule when we cannot easily determine it with usual techniques.
Chapter 6: Polymers
Nowadays, we find polymers everywhere. They can be solid or flexible, resist to low or high temperatures but are generally lighter than the materials they replace. For instance, wood or metallic chairs are advantageously replaced by plastic chairs. Plastic bags are in every shop (yet also in oceans or forests) and can support heavy charges without problem (when they break, it is usually because of a cutting edge). The development of the polymers was truly a revolution in our lives and we can difficultly imagine a turn back.
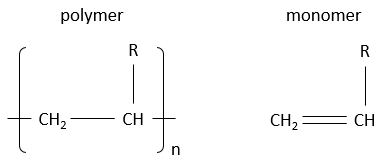
Polymers are derivatives from petroleum and are made of small blocks called monomers. Monomers are small molecules, usually gaseous, wearing a functional group that can give some properties to the polymer. The monomers composing a polymer are added one by one to the polymer that grows in length. We will see the reaction a bit later. Due to their huge size, the polymers are solid. To write the formula of a polymer, we write the smallest constituting block between brackets, that block being present n times in the polymer. Note that for one reactor, the lengths of the produced polymers are not all identical. We will obtain a distribution of size and n is thus not a fixed value.
Here are some of the usual polymers and the monomers they are made of.
The properties of a polymeric material are given by the interactions between the chains of polymer. Chains can be linear of branched. It is possible to make polymers with several different monomers. There are several ways to obtain such polymers. The monomers in the chain can be put
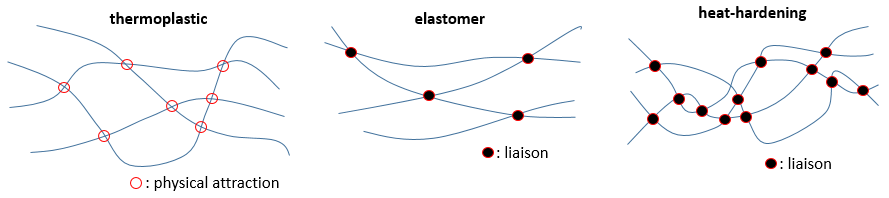
As written above, the properties of the polymers depend on the interactions between the chains. If there is no interaction at all, the chains freely move along each other, without resistance and if we stretch the material by two opposite sides, it will expend and break. The same happens if chains have physical attractions between each other. Those can easily be broken by a heating or by force. This kind of material is called thermoplastic.
Liaisons can be made between the chains. If there are only a few of them, when we stretch the material it will expend up to a point where the liaisons block any further movement. They prevent the material to break as easily as a thermoplastic one. Such a material is called an elastomer.
If there are more than a few liaisons, the material becomes more rigid and the rigidity increases when we heat it up. It is called a heat-hardening material.
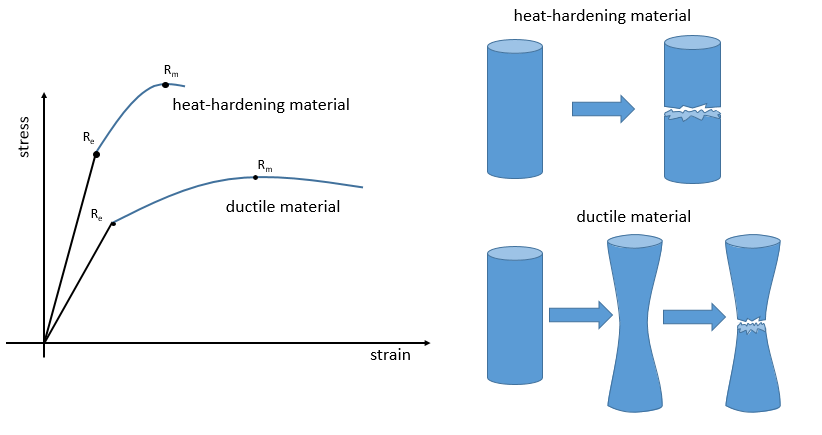
Stress-strain curve
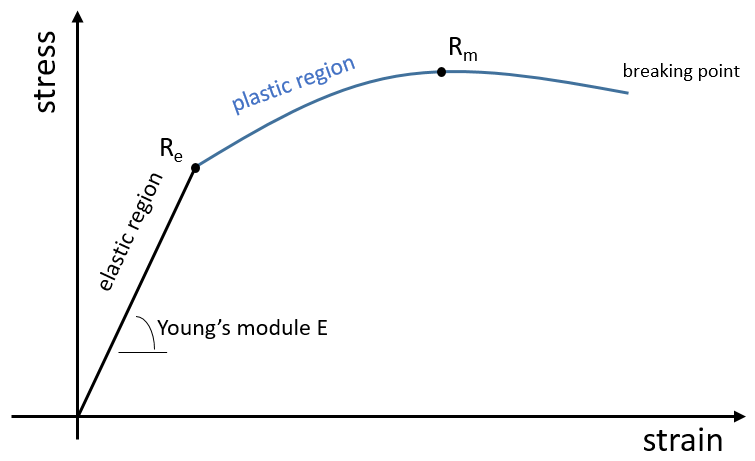
The elasticity/rigidity of polymers are determined by a stress-strain curve. A machine stretches the material while the applied force and the stretching (or strain) of the material are measured. The material should have the geometry of a cylinder to avoid problems related to symmetry. Instead of force, we measure the pressure (or stress) R=F/S where S is the surface of the base of the cylinder.
In a first time, the deformation is elastic and the variation of the length of the sample ΔL is directly proportional to the applied force F. The slope of this curve gives the module of Young E that is a characteristic of the elasticity (in the given direction) of the material. If the force was to be removed, the material would get back to its initial form. It is thus a reversible process.
Next, the curve softens and the deformation is no more an elastic deformation but a plastic deformation: the material is deformed by the applied force and cannot get back to the initial state. The variation of slope can be slight or massive. This region is called the strain hardening region and the point where the slope changes is called the elasticity limit Re. The curve should rise up to a maximum Rm called the ultimate tensile strength. Yet all the nodes don’t always break at the same time and we can see the apparition of plateaux on the curve. At Rm, the liaisons binding the polymers are all broken. The experiment continues until the material is broken in two distinct pieces.
The ductility refers to the way a material breaks. Heat-hardening materials breaks at once, after a short elastic region (with a large Young’s module E): because of all the liaisons, the material is not flexible but when the stress is large enough, the material breaks directly in two pieces. In the case of ductile materials, the sample becomes thinner and longer before the fracture. As a result, the curve continues further after Rm.
The parameters that influence the properties of polymers are
- The temperature: by the interactions between the chains. At some point, called the temperature of glass transition TG, the properties of the polymer change drastically. The temperature of glass transition TG is an interval of temperature characteristic, for a given material, of the transition between a solid and breakable state and a flexible and elastic state. TG depends on all the following parameters and on the pressure.
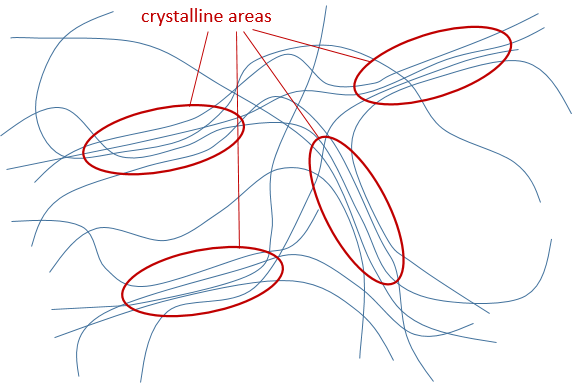
- Crystallinity: it refers to the order in the solid. The interactions and the density in the polymer are not identical everywhere in the material. The crystalline areas are areas where the chains are well packed and have strong interactions. The chains in amorphous areas are not well packed. One single chain can be simultaneously in an amorphous area and in a crystalline area.
- Length of the chains: it increases the amount of interactions
- Monomer(s): the group that the monomer wears influences the interactions between the chains
- Reticulation: it is the amount of chemical liaisons that we make in the material
- Speed of deformation: an elastic material can break if we stretch it fast enough
- Additives: we can add some molecules in the material to bind the chain together, or to avoid it to happen.
Synthesis
There are several ways to make polymers. We can subdivide them in two types: the polyaddition and the polycondensation. The difference is that there is that the Polyaddition only generate the polymer while the polycondensation also generate small molecules.
Polyaddition
It can be subdivided in two big categories: radical polymerisation (uncharged polymerisation) and ionic polymerisation (anionic, cationic or coordinative polymerisation). They are all similar in the process and we will only show the radical polymerisation here.
The synthesis is composed of 3 main steps: the initiation, the propagation and the termination step.
Initiation step
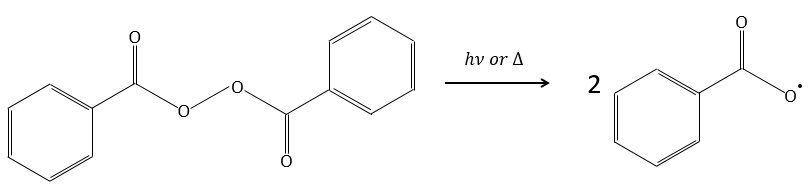
An initiator is mixed with the monomers. In the case of the radical polymerisation, the initiator is a radical. This radical can be generated by thermal decomposition or by photolysis.
For instance, benzoyl peroxide (BPO) can be homolytically cleaved by an elevation of temperature or by a laser of a given frequency.
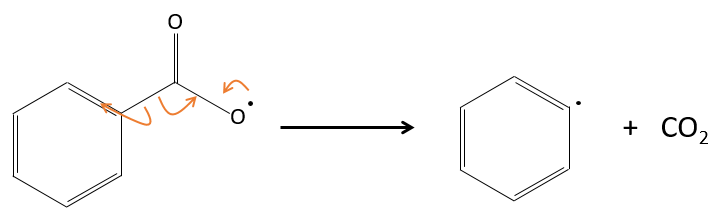
In fact, the produced radical rearranges to free CO2.
The radicals react with one monomer, transferring the radical to the other side of the molecule.
From that point, we have a beginning of chain that wears a radical and that is able to attack monomers. It is the propagation step:
As there is still a radical at the end of this reaction, it goes on and on, increasing the length of the chain by one monomer each time the reaction takes place. A chain stops to grow when the radical is neutralised. It is the termination step. During this step, two growing chains react together. It can happen two ways:
Termination: the two chains merge together
Disproportionation: the ends of the chains wearing the radical have a redox reaction together. As a reminder, the usual disproportionation reaction is a specific type of redox reaction in which a species is simultaneously reduced and oxidised to form two different products.
In the case of polymers:
![]()
Polycondentation
The process is quite different from the polyaddition. In this case, the monomers wear a functional group at both extremities. The functional groups can react with the ones of the other monomers to condensate together. For instance, a carboxylic acid condensates with ah alcohol to form an ester and water.
If the alcohol was replaced by an amine group, we would obtain an amide that is also the usual bound between peptides and thus called a peptide bond.
The production of polymers is an exothermic process: we create new bonds. However it decreases the disorder as there are less molecules in the system. As a result, the production of polymers has to be performed in a given range of temperatures. The temperature can be approximated from the type and the concentration of monomers. Indeed, except at the very beginning of the reaction, we have that the concentration of two polymers of similar sizes are approximately equal.
Chapter 5 : Kinetics – speed of reaction
Kinetics
Kinetics is a field of the chemistry that studies the speed of reactions. The speed of a reaction can depend on the conditions of the reaction. For instance, when we put H2(g) and O2(g) we don’t produce water spontaneously.
This reaction has a very negative ΔG0. However, if we produce a spark, the reaction will go very fast.
We have seen that the temperature has an influence on the equilibrium of reactions. At SCTP, the formation of ammonia has a negative ΔG0 but it becomes positive for temperatures larger than 434K.
Without temperature variation one reaction can be speeded up if we use a catalyst. We will discuss catalysts later in this chapter.
It can thus be important to know the speed of reactions in function of several parameters in order to optimise the production of one particular molecule, the destruction of some waste or any other process.
Speed of reaction
The speed of a reaction is the variation of concentration of the involved species in function of the time. It is always positive. As there can be several different stoichiometric coefficients, we have to agree on the definition of the speed of a reaction because the concentrations don’t vary the same way. To obtain this speed, we divide the variation of concentration over time of the corresponding species by the stoichiometric coefficient. In the reaction
we consider only one speed of reaction which is
The concentrations of reactants decrease over time and the speed is of the opposite sign than the variation of their concentration.
During the reaction, the speed depends on the concentrations of all the involved species.
The coefficients α, β and γ are the order of the reaction with regard to the corresponding species. α is the order of reaction with regard to NO2, β to NO and γ to O2. The order of the reaction with regard to one species is often their stoichiometric coefficient but not systematically. The sum α+β+γ is the global order of the reaction.
At the equilibrium the speed of the reaction in one direction is equal to the speed of the reaction in the other direction.
It is not true to say that v=0. The two reactions have the same speed.
At the beginning of the reaction, we can neglect the concentrations of the products in the expression of the speed with β=γ=0. The speed at the beginning of the reaction is thus simply
Integral method
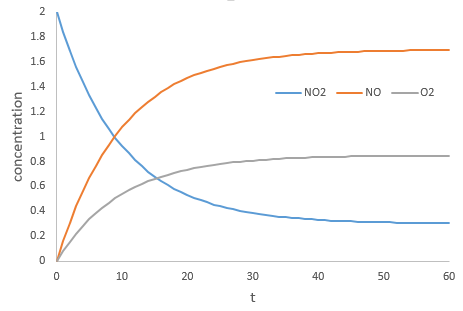
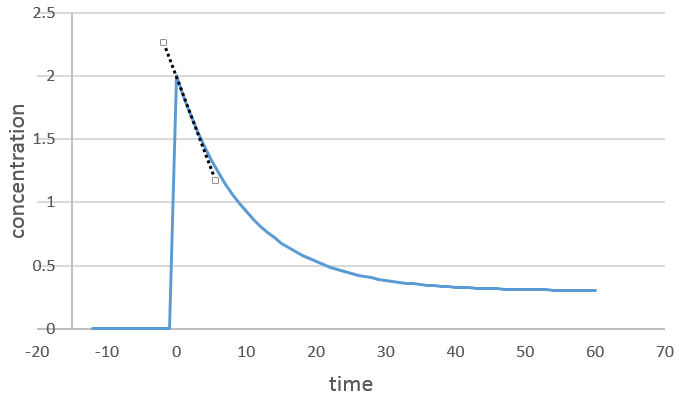
We can determine the order of the reaction with regard to one species by keeping constant the concentrations of the other reactants. Basically, we put a large excess of reactants except for the species that we want to study. This way, only one concentration varies significantly. During the reaction, we detect the variation of the concentration of the target species over time.
We focus on the period of time just after the beginning of the reaction. Before it, there is no variation to be detected (the reactant is probably not even in the solution) and later the products can play a role in the speed of reaction.
If the reaction is of order 1 with regard to the target species, the speed is
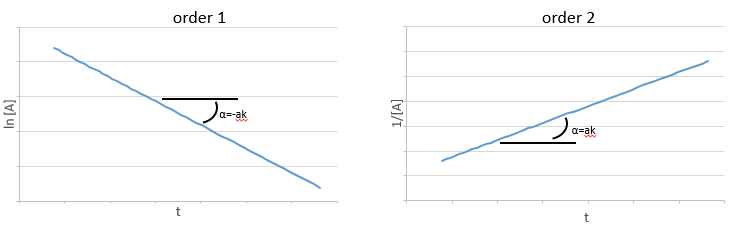
And thus we can find a straight line when we plot ln[A] in function of the time, the slope of which is –ak
If the order=2, the ln[A] won’t give a straight line but 1/[A] does. In this case, the slope is ak.
The order can also be equal to zero, meaning that the concentration of the reactant does not matter (except for very small concentrations). That means that the reaction is limited by something else. We often observe order zero reactions in presence of catalyst.
A catalyst is a species that affects the reaction but is not consumed during the reaction. The most common catalysts are solid but some catalysts are liquid. On solid catalysts, the reactants can bind on the catalyst. Because of this new liaison, the liaisons in the reactant are weaker and the reactivity is improved. The reaction is thus limited by the available surface on the catalyst. The solution is mixed during the reaction so that there is always reactants in the vicinity of the catalyst. Otherwise the reactants would be further and further of the catalyst as the time goes on. The evolution of the concentration would be more complex in this case. We will discuss furthermore about catalysts later.
Method of the initial speeds
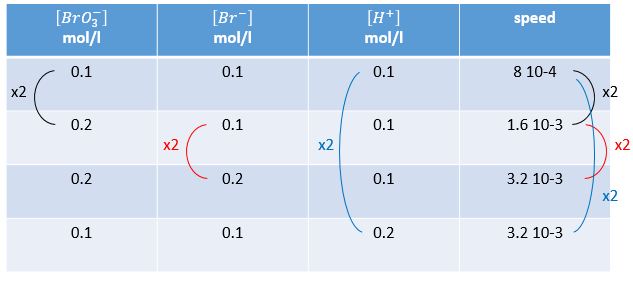
Instead of using excesses of reactants, we can do several experiments and vary one concentration each time. The reaction
is obviously not a simple reaction. The speed depends simultaneously on the three reactants BrO3–, Br– and H+. We first do the reaction with identical concentrations [BrO3–] = [Br–] = [ H+] = 0.1M. We analyse the evolution of the concentration of one species as a function of time and we only consider the variation of concentration directly after the beginning of the reaction to determine a speed of the reaction.
In a second time, we do the same reaction but modify the concentration of one reactant. The speed of reaction will change consequently and we can determine the order for each species. Ultimately when we know every order we can determine the value of k.
Model of collisions
The reactions are decomposed in elementary events. In this case the order is the stoichiometric coefficient (usually 1 or 2). Elementary events are reactions that are done in one step: everything is done during the collision between the two molecules.
For instance, the reaction between the carbon monoxide CO and NO2 is an elementary event: the oxygen atom is transferred from NO2 to the CO during a collision between the two species. When the impact occurs and the molecules were in the good orientation, the liaison N-O weakens and simultaneously a liaison is formed between C and O
The collisions between molecules don’t always lead to a new product and there are some conditions for the reaction to happen. The intermediate of reaction OCONO can be obtained only if the collision comes from a given angle: the intermediate is linear. In addition to this spatial limitation, to transfer the atom of oxygen, the liaison between O and N needs to be stretched, requiring some energy. Finally there is a variation of the number of moles of gas during this reaction: NO is a liquid and therefore there is a decrease of entropy that has to be overpassed.
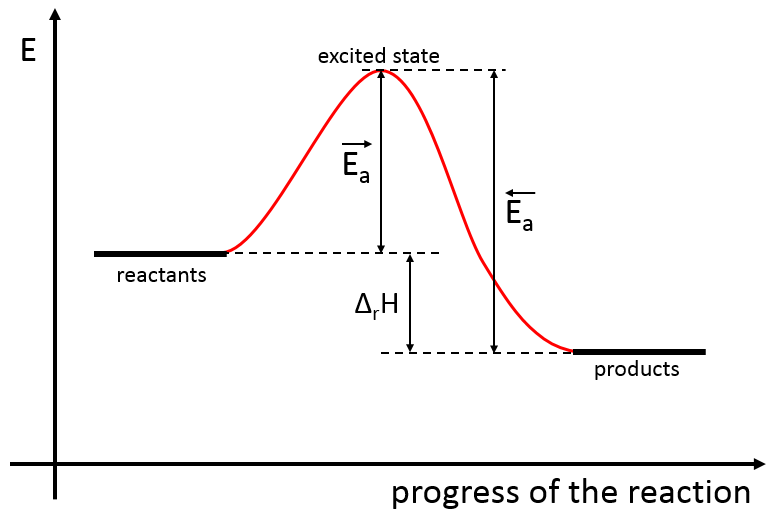
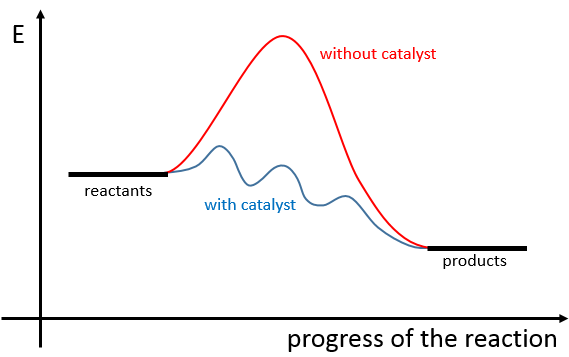
There is thus a minimum of energy that is required to obtain the reaction. This energy is called the energy of activation. One can represent the evolution of a reaction this way:
The reactants, taken separately have a given amount of energy. The products of the reaction have a lower energy. The difference of energy between the products and the reactants is the enthalpy of reaction. To obtain the products, the energy of activation is similar to a barrier that has to be climbed. At the summit of this barrier is the excited state, called this way because it is high in energy. After the excited state, the energy decreases down to the products energy that should be lower than the energy of the reactants.
To do the reaction in the other direction, forming CO and NO2, the energy of activation is much larger and the products are energetically less favourable. The difference between the two energies of activation is also equal to the enthalpy of reaction.
To surpass the energy of activation, the molecules must have enough kinetic energy. If it is the case, they do successful collisions. Remember that the kinetic energy of molecules depends on the temperature. If the temperature gets higher, a larger population of the molecules will have a kinetic energy larger than the energy of activation.
In the expression of the speed of reaction, we find these dependencies in the constant of speed k
The energy parameter is in the exponential and the spatial parameter and the frequency of the collisions are found in the constant A.
Note that slow molecules can also react if they have a large potential energy, for example a lot of energy of vibration. Instead of the kinetic energy, the potential energy is used.
As a result, if two NOBr are correctly aligned, they can form Br2 even if their kinetic energy is low because of the vibration of the liaisons Br-N.
Eventually the N-Br liaisons can be stretched simultaneously, approaching the two Br from each other and facilitating the formation of Br2.
The speed of the reaction to form hydroiodic acid from hydrogen and iodine may let us think that it is an elementary reaction.
Indeed, the exponents of the concentrations are the stoichiometric coefficients of the reactants. However, this reaction is not an elementary reaction. To have been one, the molecules would need to be aligned in one specific way and the liaisons have to break and to form at the same time. It means that 4 events have to happen at the same time in addition to the specific angle of collision.
Yet the reaction is done with a speed that let us think about an elementary event. The complete reaction is the succession of elementary events occurring one after each other.
The first step is the homolytic dissociation of I2. It is done with the help of a catalyst metal.
It was observed that the composition of the recipient can affect the speed of the reaction. The dissociation is thus done at the surface of the recipient. After the dissociation, I can now react with H2 to form H2I that can react with the second I from the first reaction to produce 2 HI.
While the last reaction is complete, the first and second reactions are reactions of equilibrium and can thus go in both directions.
The speed of the global reaction is determined by the slowest elementary event. This slow step is called the determining step and is here the last reaction:
How do we find that this speed is equal to the one obtained experimentally?
To obtain such a thing, we use two hypotheses:
- the equilibrium reactions are almost at the equilibrium: the third reaction is slower than the two first reactions and we assume that the difference of speed is such that the first reactions (almost) have the time to reach the equilibrium. As a result, we can say that for those two reactions, the speed in one direction equals the speed in the opposite direction
The ratio between the constants of reaction k1/k-1 is the global constant K1.
We can do the same for the second equation:
We can now replace the concentrations of v3 with the expressions that we found just now
The constant that was found experimentally is thus a combination of the three constants of reaction.
- the concentration of H2I is constant:
H2I is the product of the second reaction and the reactant of the third reaction. By this assumption, we assume that as soon as H2I is produced, it will be consumed by the next step of the reaction or turns back into H2 and I by the reverse of the second reaction.
We can insert this in the expression of v3.
Given that v1=v-1 (from the first hypothesis), [I]2=K1[I2] and
We have here the same expression than the one we obtained with the first hypothesis in the numerator. We can thus make the assumption that the concentration of H2I is constant if k3[I]/k-2<<1, i.e. that the concentration of I is small and that k3<<k-2. It is thus only correct at the beginning of the reaction.
We might think that the hydrogenation of Br2 follows the same kinetics but we are far from the true. Indeed,
This reaction is also a series of elementary steps
Catalyst
A catalyst is a species that is involved in a reaction but is not consumed or produced during the reaction. It helps a reaction to take place by a diminution of the energy of activation.
A catalyst can be in the same phase than the reactants, in this case we talk of a homogeneous catalyst, or in a different phase, as for the reaction between I2 and H2 where the catalyst is the surface of the recipient, a solid. In this second case, we talk of a heterogeneous catalyst. There are at least 4 stages for the action of the catalyst. We will see them through the catalytic hydrogenation of the ethylene.
- adsorption and activation of the reactants: the species that are in the vicinity of the heterogeneous catalyst may bind to it. In term of entropy, the binding is quite neutral: the species comes from a liquid to bind on a surface where a lot of spot are possible. There is thus a lot of possible configurations on the surface.
- Migration of the reactants on the surface: the reactants must be near to react together
- Reactions
- Desorption of the products
In the case of a homogeneous catalyst, the catalyst is just a species that intervene during the reaction but is not consumed by it. In high levels of the atmosphere, NO acts as a catalyst in the destruction of the ozone.
Case of the ozone
The formula of the ozone is O3. This molecule is sensible to UV beams that breaks it into O2 and a radical O.. A radical is a species or a molecule that has has unpaired valence electrons and that is very reactive. They are usually the result of a homolytic dissociation, i.e. the electrons of the liaison are equally shared between the two atoms. It is so reactive that it can break nearby molecules to form a liaison. We use radicals to produce polymers (that will be seen in the corresponding chapter) and also in antibacterial products. The good point of using ozone as an antibacterial product is that it rejects oxygen O2 as waste, so it is clean for the environment.
The destruction of ozone is done in two steps: the first step is the dissociation of a radical O. under the beaming of UV photons.
The radical can react with the O2 (reverse reaction) to get back to ozone or react with another ozone molecule to form more O2.
In total, we obtain 3 O2 from 2 O3 molecules.
The radical O. is not a catalyst of the reaction even if we don’t find it in the global reaction because it is produced and consumed during the reaction. It is not a species that is already present in the system from the beginning and that remains in the system once the reaction is complete. The speed that we find experimentally is
It is not the speed that we could expect from a one step reaction. We can do the kinetic analysis of the reaction. The determining step of this reaction is the second reaction.
The concentration of the radical is difficult to determine, but we can still make the same assumptions we made with the reaction between H2 and I2: the concentration of the intermediate product doesn’t change and the first reaction is at the equilibrium:
We can insert this in the expression of the speed
Freon’s
Freon’s are small species full of halogens, CCl2F2 for instance that have a very high heat capacity and are nonpolar and inert. There have been used as refrigerant in the fridges for a long time and we thought that, as those species were inert in the labs we had no specific care to apply to them. However Freon’s are deteriorated by UV rays. In dumps, the tubes containing the Freon eventually break and the gas goes up high in the atmosphere where it is not inert anymore. The deterioration of Freon’s due to UV’s leads to the formation of radicals that will interact with the ozone.
If we sum the two last equations, we get the determining step of the deterioration of the ozone alone.
The Cl. is thus a catalyst of the destruction of the ozone and the hole in the ozone layer started to grow. The problem is that the Freon gas takes a very long time (years) to reach the higher atmosphere and at the moment we observed their effect, a lot of Freon’s were already climbing. Now the use of Freon’s is forbidden and the hole in the ozone layer is slowly decreasing in size.
Another product having an effect on the ozone is some nitrogen products of the exhaust pipes of cars. During the combustion of the fuel, nitrogen monoxide and dioxide can be formed.
Nitrogen dioxide is deteriorated by light.
Low in the atmosphere, and at the ground level, NO acts as a catalyst and generates peaks of ozone. Higher, NO catalyses the destruction of the ozone.
Chapter 4 : Kinetics – Equilibrium
Chemical kinetics is the study of the speed of reactions. The speed of reaction is determined by the variation of the quantity of species by unit of time. Usually, we consider the concentrations for species in solution and we consider pressures for gases.
The speed of a reaction is rarely constant and is positive until the system reaches the equilibrium. At the equilibrium, the speed of reaction is zero.
Equilibrium
Given a reaction
The equilibrium is reached when the concentrations of the species don’t vary anymore over time. The constant of equilibrium K, that expresses the law of mass action, is
The constant of the reversed reaction, from right to left, is K’=1/K and if we consider a multiple n of this reaction,
K’’=Kn because stoichiometric coefficients are as exponents in the expression of the equilibrium constant.
The units of K depend of the reaction. For instance, the reaction of Haber that generates ammonia and that we already met before
has an equilibrium constant Kp that depends on the pressures of the reactants and products.
The units of K depend thus on the amount of different products and reactants and on their stoichiometric coefficients. We denoted the constant with a p because we usually consider equilibrium constants in term of concentrations, that we can denote Kc. There is a relation between Kc and Kp that we find from the law of perfect gases pV=nRT
The relation between the pressure and the concentration is thus simply a multiplication by RT. In the expression of K, this RT is also at the power of the stoichiometric coefficient.
For the reaction of Haber, we find
In the case of condensed phases, we won’t consider the concentration nor the pressure because interactions between the species have to be taken into account. We consider the activity of the species instead. The activity reflects the ability of a substrate to react. In condensed phases this ability is decreased by the interactions with the nearby molecules. The activity is proportional to the concentration of a species or to its pressure, multiplied by a coefficient γ. The equilibrium may be heterogeneous if all the species intervening in the reaction are not of the same phase. In this case too, we consider the activities of the species instead of their concentration or pressure. For instance, the reaction
is a reaction where two solids and one gas coexist. It has the following constant of equilibrium:
We choose on purpose a reaction involving solids because their activity is equal to 1. The constant is thus simply proportional to the pressure of CO2. In a closed system, this reaction won’t produce more product if we increase the quantity of reactant. The reaction is only limited by the pressure of the gas.
The reactive quotient Q
To determine the direction of a reaction, we compare the constant of equilibrium K with the reactive quotient Q. Q is determined from the initial concentrations put in presence.
For the reaction
The quotient Q and the equilibrium constant K are respectively
If we consider a system of 5l containing the following quantities of each species:
Given that there is no product in this composition, the reaction will obviously go toward the right. It is impossible to obtain negative concentrations. The reaction will proceed until it reaches the equilibrium or that all of one reactant is consumed. We can determine the concentrations of each species at the equilibrium with the following method:
We determine the concentrations of the species. Here we gave the volume of the recipient and the number of moles of each species. We write them in a table and assume that a concentration x will be consumed to reach the equilibrium. The same quantity (in stoichiometric ratios) of product has been formed.

As we know the value of K, we can determine x and thus the concentration of each species.
This equation of the second order gives two solutions but one is negative and thus impossible (no negative concentrations). We can thus determine the concentrations at equilibrium for all the species.
If K is small, for instance in the reaction
has K=1.6 10-5 mol/l, it means that the reaction does not consume a lot of reactants. If we begin the reaction with only 1 mole of NOCl(g), we will consume 0.03mol/l of it.
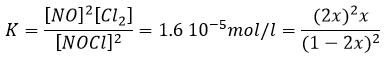
Assuming that x is small, the lower part of the fraction is simplified and
The assumption that 2x<<<1 is correct. A small equilibrium constant also means that the reverse reaction is more favourable (K’=1/K).
Temperature of inversion
The equilibrium depends on the temperature. We have seen in the thermodynamics sections that
At a given temperature, the reactions goes in one direction but if we increase the temperature enough, the reaction will go in the opposite direction. The temperature at which it occurs is the temperature of inversion and is when
If the reaction is performed at p=1atm, we can find this temperature from the tables of ΔH0 and ΔS0:
Modification of the equilibrium
Now, if we consider a system at the equilibrium and we apply a modification on this system, Le Chatelier enounced that the equilibrium will change to counterbalance this modification.
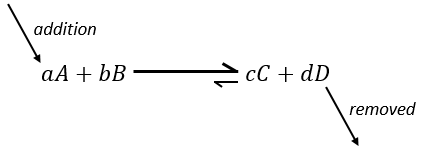
–addition of a substrate: the equilibrium will consume more of this constituent or produce less of it
For instance, let’s consider a reaction at the equilibrium
if we add more A in the system, the equilibrium is displaced to the right to consume some of the added reactant
If we added some C (a product) instead, the equilibrium would have been displaced to the left.
Another way to modify the equilibrium is to remove the products out of the system to displace the equilibrium to the right.
To optimise the speed of a reaction, we can thus add reactants and remove the products continuously.
–temperature: the equilibrium depends on the temperature, as we have seen above. The effect will be different for an exothermic reaction or an endothermic reaction. Indeed,
The variation of temperature affects the exponential with ΔH0. If ΔH0<0, i.e. it is an exothermic reaction, K decreases as result of an increase of temperature and the reaction is thus less efficient. During an exothermic reaction, heat is a product of the reaction
and the temperature increases the heat so the equilibrium is displaced to the left. If the reaction is endothermic (the reverse reaction for instance), an increases of temperature helps the reaction to proceed (more heat is available to be absorbed). The equilibrium is thus displaced to the right.
–pressure/volume: during reactions involving gases, a diminution of the volume will displace the equilibrium toward the side where there is less moles of gas. In the previous reaction, the equilibrium would be displaced toward the right because we generate 2 moles of gas from 4. We can also displace the equilibrium by the addition of an inert gas that will increase the pressure without any modification on the chemical reaction.
Experimental determination of K, ΔH0 and ΔS0
We know that the equilibrium is displaced by a modification of temperature. Imagine that we want to know the values of K, ΔH0 and ΔS0 of a dissolution process like
We know that if there is no Ag+ or Cl– in the solution before the reaction, their concentration will be equal as one of each ion is produced during the reaction. As solids have an activity a=1, the constant of dissociation Ks is
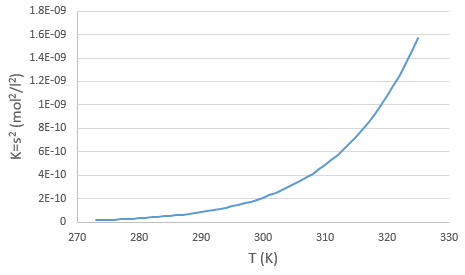
The concentration in ions is thus equal to the square root of the dissociation constant. At a given temperature, we can thus measure the concentration at the equilibrium of one of the ions to determine the value of K. We can repeat this experiment at several temperatures and plot the relation between the temperature T and K.
We see that the dissociation constant Ks increases with the temperature, meaning that if we increase the temperature, we can dissolve more AgCl in solution. AgCl is not very soluble in water: only mg of it per litre will dissolve (the square root of Ks gives the concentration). But we can find more information from this relation. We know that the equation connecting K and T:
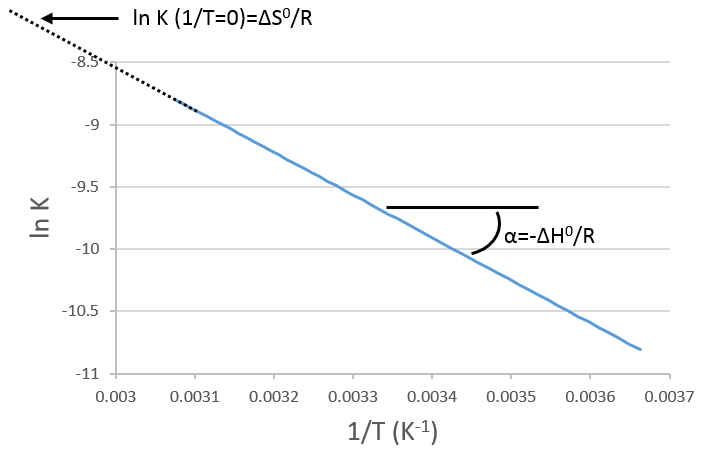
If we plot ln K in function of 1/T, we find a straight line the slope of which is –ΔH0/R.
The intersection with the axis at 1/T=0 will give us ΔS0/R. On the figure, the axis is not at 1/T=0 and the intersection of the curve with the axis doesn’t mean anything.
In the living, ΔG is usually very close to zero so that a stimulus can allow a reaction to take place. In our body, several reactions that would normally not work are coupled with the phosphorous removal of an ATP to allow the process to take place. The ATP is a reserve of energy of our body.
Chapter 3 : Methods of separation – extraction
Methods of separation
One job of a chemist is to analyse samples of chemicals. To determine the composition of the sample, a separation of the different elements is necessary to avoid interferences between the species.
It can be of importance to determine which chemical elements are present, in which quantities and oxidation state. Several methods of separation can fulfil the needs of the chemist to obtain a good separation. In most of the cases, the sample must be a solution the solvent of which does not contain any interfering species.
The separation methods are based on the affinity of species for different solvents, on equilibrium processes and on kinetics. Some methods allow to get the sample back and some destroy it.
Extraction
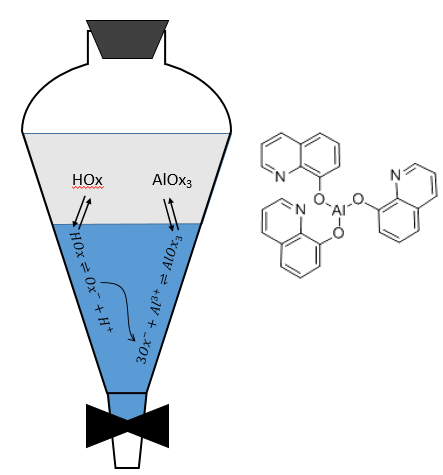
This method is based on the affinity of species with two different immiscible liquid phases. One phase is aqueous and the second one is organic. The experiment is performed in a separatory funnel (or sep funnel). It is a piece of glass or plastic shaped like a reversed cone with a valve on the bottom and an opening at its top. A cap can close the funnel to allow a vigorous mixing.
The sample is prepared in one of the two phases and is placed in the extraction funnel by its top opening. The second phase is added (the order of insertion of the two phases does not really matter). As the phases are immiscible, the exchanges of particles between the phases can only be made at the interface and charged species do not move into the organic phase: their solubility in any organic phase is very low. To improve the exchanges, the liquids are mixed by shaking the funnel and by turning it upside down. It increases the surface of contact between the two phases, thus the exchange is improved. During the mixing phase, it is recommended to open briefly the funnel (by the cap or by the valve) to release an eventual excess of pressure. Remember some security notions: it can be necessary to open the funnel under a hood and do not put your nose or an eye just above the opening when you release the pressure. Next, the system is put to rest until the interface is thin and clear. The phase of lowest density is at the top and the densest is at the bottom. Usually, the organic phase it above the aqueous phase because the density of organic solvents is usually lower than the density of the water (oil floats on water). We can thus remove the aqueous phase out of the funnel by opening the valve at the bottom of the flask.
Distribution of the species
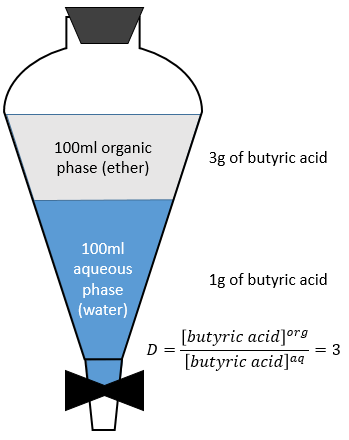
At the equilibrium, each species is distributed between the two phases. We can define a coefficient of distribution KD that is the ratio between the concentration of a species in the organic phase and in the aqueous phase:
If we don’t specifically consider the equilibrium, it is the distribution ratio D.
![]()
For the concentrations of the species, we consider all the form of a given species. Reactions often depend on the solvent and may occur in one phase but not in the other one. For instance, an acid in the aqueous phase can be in its acidic form HA or in the conjugated base form A–. The solubility of ions in organic phases being very low, the exchange of species between the two phases is limited to HA.
As a result, A– is not exchanged and remains in the aqueous phase while the neutral species HA has a concentration balanced between the aqueous phase and the organic phase. So, the distribution ratio of the acid is
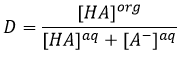
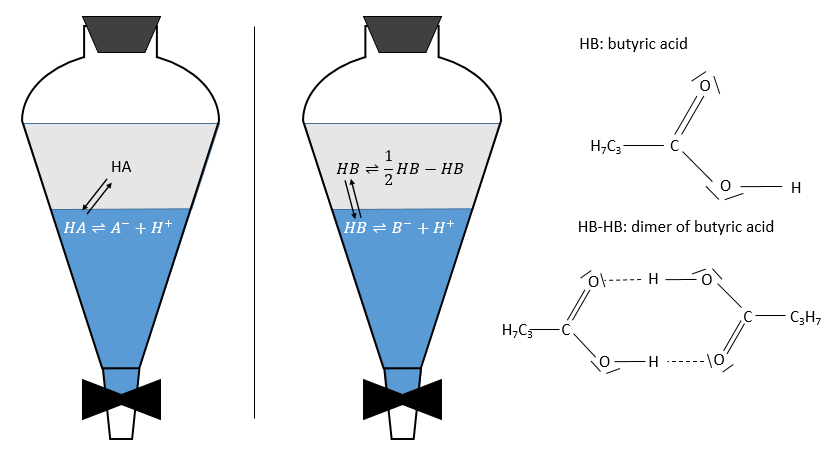
As a result, the distribution ratio may depend on the acidity of the aqueous phase. Equilibrium reaction can also specifically occur in the organic phase, as it is showed with the example of the butyric acid HB (see the right of the previous figure). In the organic phase, this carboxylic acid can form a dimer HB-HB, connecting two HB together by two hydrogen bonds. The dimer is stable in the organic phase but it is not the case in the aqueous phase where the acid can lose its proton. In this case, the distribution ratio will be
The choice of the solvents is thus crucial for a good extraction. The solvents can be polar or nonpolar depending on the separation that has to be done, but they must not be miscible.
Extraction of organic species
To extract an organic compound out of the organic phase, we want to get charged species. The neutral species are shared between the two phases but the ions remain in the aqueous phase. If the compound is not ionisable, we can only play on the nature of the solvent to expect the best extraction, i.e. when KD is small. If the compound can be dissociated, we can tune the acidity of the aqueous solution to optimise the extraction.
The acetic acid has a pKa of 4.7.
![]()
At this pH, in the aqueous solution, there will be as much CH3COOH as CH3COO–. The acetate can be extracted in the aqueous phase. If we use a stronger acid, a majority of the acetic acid that penetrates in the aqueous solution will dissociate to form acetate that can be extracted.
Another case is the case of amphoteric species. These species can play de role of a donor or an acceptor of proton. The oxine (8-Hydroxyquinoline) is an amphoteric.
At pH<5, the nitrogen is protonated, giving a positive charge to the compound that can now be extracted. At pH>10, the hydroxyl group loses its proton, leading to a negatively charged species that can also be extracted.
Between 5<pH<10, oxine remains in the organic phase.
Extraction of metals
The metallic cations can be extracted from aqueous solutions. In this case, we want to obtain a great value of D. To transfer the metals from the aqueous phase, their charge has to be hidden by the formation of strong ionic pairs or by the formation of coordination complexes. The oxine can form a complex with metals to stabilise them in the organic phase. For instance, if we want to extract aluminium from an aqueous solution, the oxine can travel from the organic phase to the aqueous phase. In good conditions of pH, the oxine loses its proton. In its basic form, the oxine forms a complex with the ions of aluminium, a complex that can now be transferred in the organic phase.
Fe3+ can form an ionic pair in a concentrated solution of HCl. The ionic pair (FeCl4)–H3O+ can move into the organic phase. Note that this product of the reaction moves out of the aqueous solution. The equilibrium is thus shifted to the right.
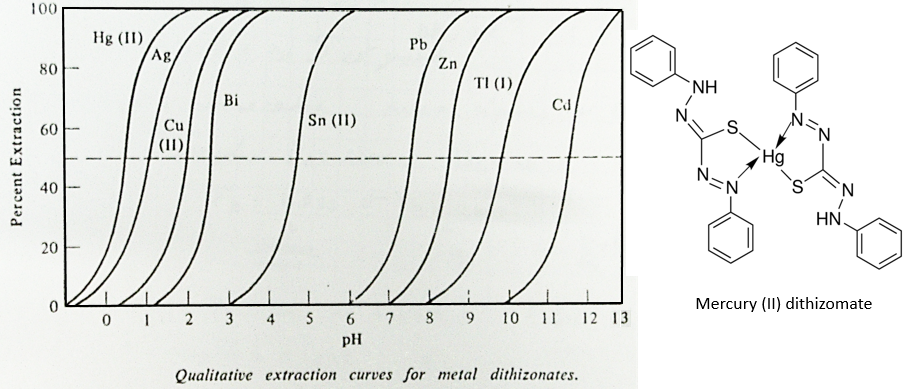
Another way to shift the equilibrium to the right is to increase the pH of the aqueous solution. It is possible to extract specifically several metals depending on the pH of the aqueous solution. The following figure represents the extraction of various metals by the formation of dithizomates in function of the pH.
One can see that the extraction of Pb starts at pH>6 while Ag is already fully extracted at pH=3. The separation of Cu (II) from Ag will require another method of separation.
Extracted fraction
Let’s consider the extraction of the butyric acid. The distribution ratio D is the ratio of its concentration in the organic phase (ether) over its concentration in the aqueous phase (water). After the extraction, 3g of butyric acid is in the organic phase and 1g is still in the aqueous phase.
The extracted fraction F is the quantity of the acid in the organic phase over the total quantity of the acid:
F=3/4 if the volumes of the aqueous and organic phases are equal. The ratio of volumes RV is the volume of the organic phase over the one of the aqueous phase. If we consider a large volume of solvent with regard of the volume of the species to separate, the initial volumes of solvents put in presence can be used with a good approximation. Injecting RV in the expression of F, we obtain the following expression:
We can conclude that an extraction has better results when D or RV is large.
The remaining fraction G is the fraction of the sample that has not been transferred to the organic phase and is simply
Now if two compounds A and B are to be separated, we have to design the experiment such as the multiplication of DA by DB is equal to 1. Indeed, if DA and DB are large but DA>>>DB, the separation will not be efficient. Image that DA=1000 and DB=20. A has a better extraction than B, but both species are extracted: the extracted fractions are, considering identical volumes of phases
Despite the huge difference of D, the separation is bad. Now, if DA=10 and DB=0.1, the extraction of both compounds is lower than in the previous example but the separation is way better:
This time, 91% of A are in the organic phase for only 9% of B.
To obtain a better separation, we can repeat the extraction starting with the organic phase we just extracted. Let’s come back to our first example of the butyric acid. For this compound, we had found D=3. We can play on the volumes of the phase to modify the efficiency of the extraction. If we put half the volume of ether, then RV=0.5. The extracted fraction will be
Out of the 4 initial grams, 1.6g are in the aqueous phase and 2.4g are in the organic phase. The extraction was batter with a larger volume of ether. However, if we do a second extraction with the same conditions, F is again 0.6 and we will have 0.64g remaining in the aqueous phase.
We have done two extractions with 50ml of ether instead of one extraction with 100ml of ether. So with the same volume, but with two extractions, we extracted more butyric acid (3.36g vs 3g). Several extractions with a small volume are thus more efficient than one extraction with a large volume. After n extraction, the remaining fraction is
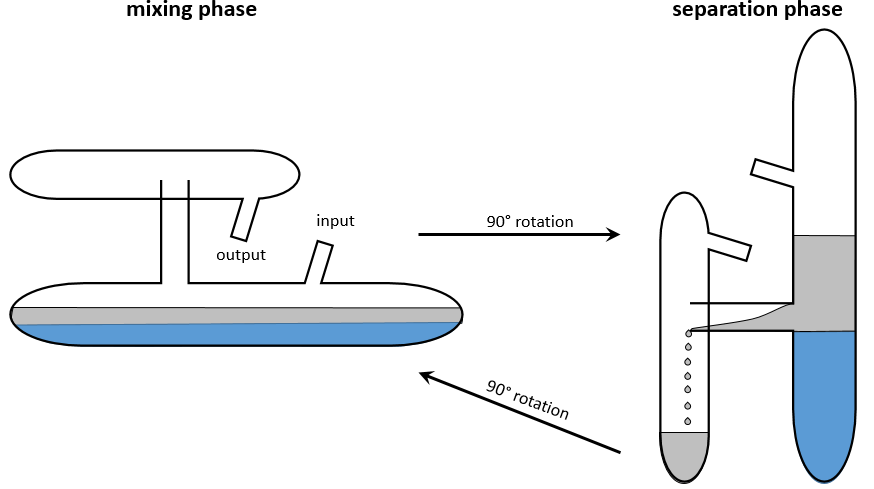
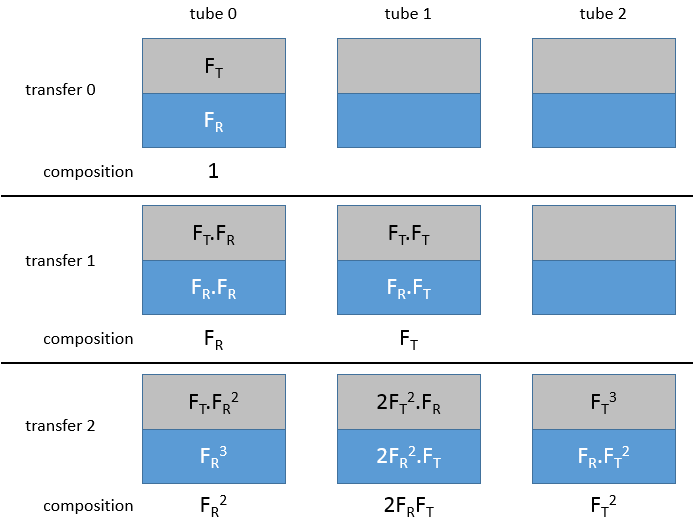
Craig Apparatus
This method has been optimized into the apparatus of Craig. Dozens to hundreds of H shaped tubes are connected. The next figure shows one tube.
Mechanical arms mix the small tubes during the mixing phase and tilt them to transfer the top phase in the small compartment of the H shaped tube. Once the transfer is done, the tubes are put back in their initial position. This rotation causes the emptying of the small compartment in the next tube. The process is repeated in all the tubes simultaneously.
Initially, the sample is in the first tube (noted 0) and the bottom phase is already in all the tubes.
Initially, all the substrate is in the tube 0, half of it in the organic phase and the other half in the aqueous phase. The organic phase is transferred into the tube 1. We can define a remaining fraction FR, that is the fraction of the sample that remains in the tube during a transfer, and a transferred fraction FT that is the fraction that is transferred in the next tube.. After the first transfer, there is FR in t0 and RT in t1. The tube 0 is now filled with the solvent and the tubes are mixed.
After the mixing in the tube 0, the remaining fraction FR is now separated in the organic and the aqueous phase. In the aqueous phase (considering that the organic phase is transferred each time), there is now the remaining fraction of the first remaining fraction, i.e. FR.FR. In the organic phase, there is the transferred fraction of the remaining fraction, i.e. FR.FT.
In the tube 1, the transferred fraction from the tube 0 is separated between the two phases. In the aqueous phase there is now FR.FT and FT.FT in the organic phase. Once the mixing is done, the organic phases will be transferred to the next tube. The aqueous phases stay in their tube. FT2 is transferred from t1 in t2 and FR.FT is transferred from t0 to t1. After the transfer, we find respectively in the tubes 0, 1 and 2, FR2, 2FR.FT and FT2.
After three transfers, we would have FR3, 3FR2.FT, 3FR.FT2 and 3FR3. You may have noticed that those values are the members of an exponent of a sum:
n being the number of transfer. In a given tube r, the fraction is
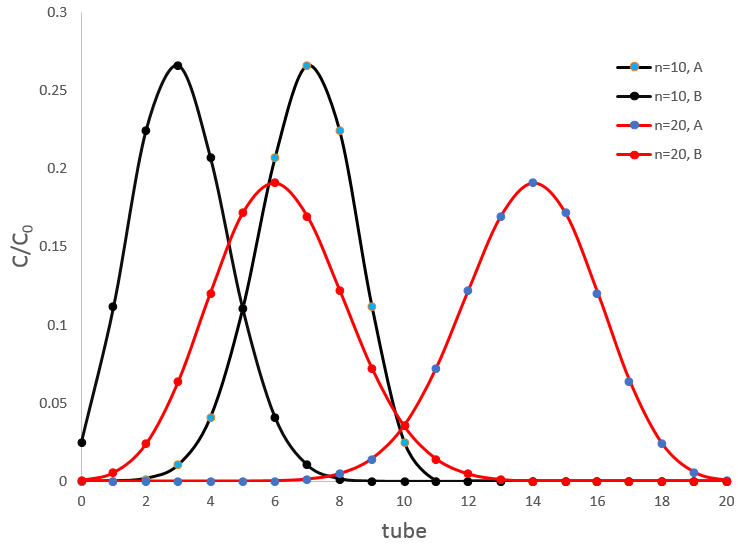
We can thus predict the composition of each tube knowing the result of one single extraction. For a large number of extraction, we find the equation of a Gaussian curve.
The width of the peak is characterised by a standard deviation
The peak moves linearly with n, spread as √n and the intensity of the peak decreases as 1/√n.
If two substrates are in the sample, the apparatus of Craig will separate them. Again, we have to choose carefully the conditions of the extraction to obtain a good separation. The figure above shows the concentrations of two species with DA=1/DB=9/4 after 10 and 20 transfers. There is an overlap between the curves where the species are not well separated but it decreases significantly with the number of extractions. At the maximum of the peak for A, after 10 transfers we find ~27% of the initial concentration of A but also 1% of the initial concentration of B. After 20 transfers, we have 19% of [A]0 and only 0.03% of [B]0.
The advantages of the apparatus of Craig is that everything is mechanical, so the precision is good and that we can either get the result of the extraction at the end of the apparatus or at one given tube in the apparatus.
Chapter 2 : thermodynamics – second and third principles
Second principle
Increase of the entropy: The entropy in the universe increases over time.
The entropy is a measure of the disorder of a system. The second law of thermodynamics has several formulations but the most common is that a process is spontaneous if, without external influence (isolated system), it induces an increase of the entropy in the universe.
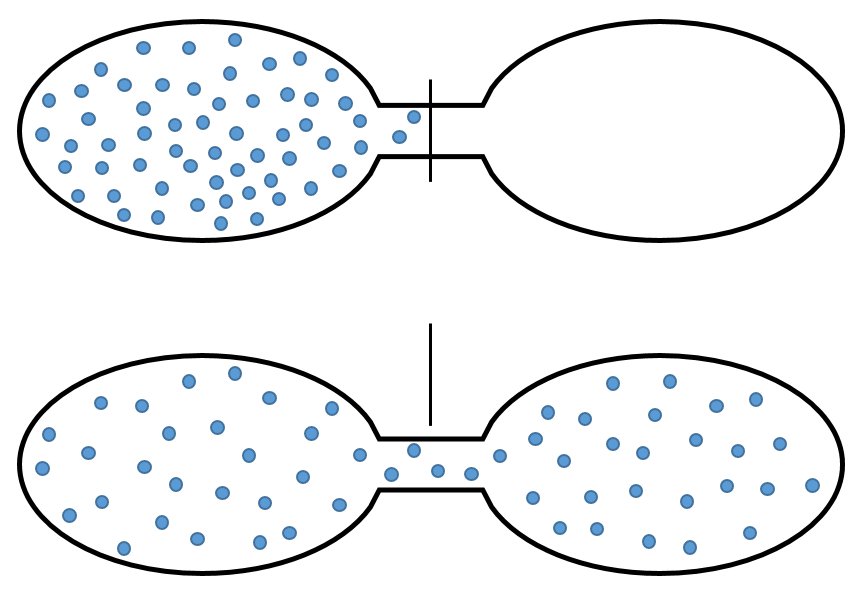
For instance, if two reservoirs are connected, one being empty and the other one full of gas, the gas will spontaneously occupy the whole system even if it does not involve any variation of energy.
The gas dilates because there are more positions to occupy in a larger volume. Another definition of the entropy is that a system tends to change to the most probable state.
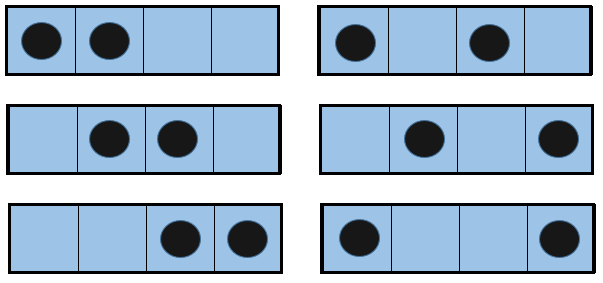
Imagine a small box with only a few available positions. Two particles are in this box and each one occupies one spot. Several combinations are possible:
If we increase the volume of the box, the amount of possibilities increases exponentially. It is an entropy of position/disposition. The formula of this kind of entropy for one particle is
Ω being the amount of possible configurations for this particle.
If the volume containing this particle changes from a volume V1 to a volume V2, the variation of entropy is
The number of positions for one particle is directly proportional to the volume and
For diluted gases, the volume of the particles is negligible with regard to the volume of the system. As a result, we can barely ignore the presence of other particles in the formula and say that for NA particles (1 mole)
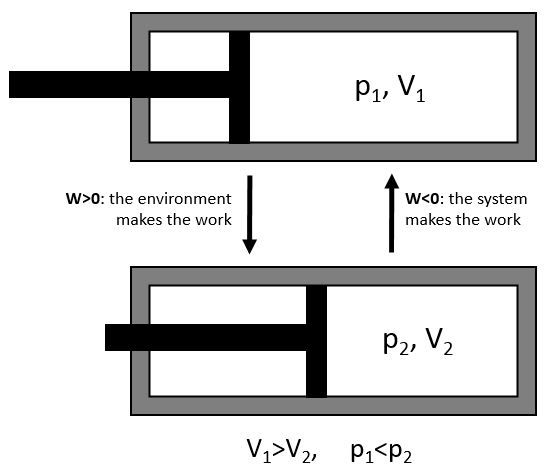
We have seen earlier the dilatation of a gas that the energy was a state function but that the work and the heat were not and thus that the way the process takes place has an influence on the work and on the heat. The third path we discussed was the isothermal process for which we found an expression for the work
This process is isothermal so ΔE=q+W=0.
We can thus find the variation of entropy for this process from the heat. If the gas dilates, heat enters the system (it is an endothermic process).
The variation of entropy is thus equivalent to the quantity of heat that the gas has to absorb to keep its temperature constant.
The states of the matter don’t have the same entropy. A gas has an entropy way larger than a liquid, itself a bit larger than the one of a solid. We can easily understand that using the repartition of particles in a small box.
In a (perfect) gas, the particles don’t have interactions between them. They can thus occupy any position of the volume without restriction. In a liquid, the particles interact together and stay grouped but the shape of the cluster is not fixed. The possibilities are thus more limited than for a gas. In a solid, the particles are fixed together in a given shape. The positions that a solid can take are thus more limited than the ones that a liquid can take and way more limited than for a gas.
Tables of standard entropies exist and give the entropy of molecules in a given state at 298K.
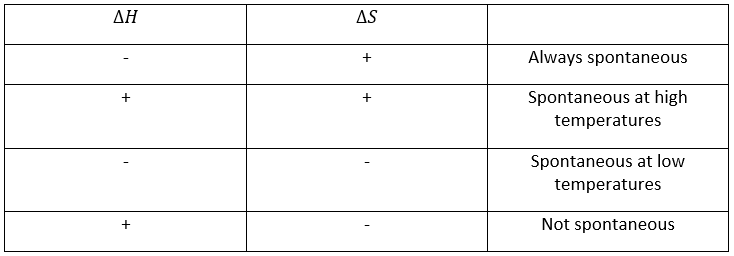
To resume, several cases can be distinguished. A process occurs if the production of entropy in the universe is positive. This production of entropy is composed of the variation of entropy in the system and in the environment. One of those components of the entropy can be negative if the other component is positive and larger in absolute value.
When a reaction produces a gas, the variation of entropy is positive. If this reaction is exothermic, heat is transmitted to the environment, meaning that its entropy increases. This reaction is thus spontaneous. If the reaction was endothermic, the variation of entropy of the environment would have been negative. The reaction could still be spontaneous if the production of entropy of the reaction is larger than the decrease of entropy in the environment.
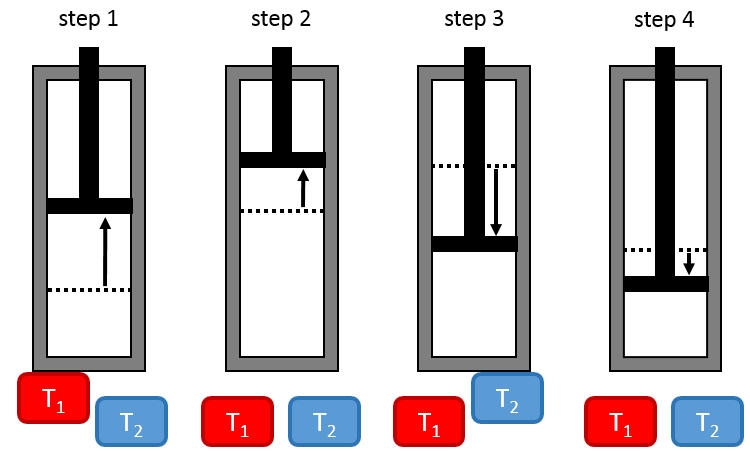
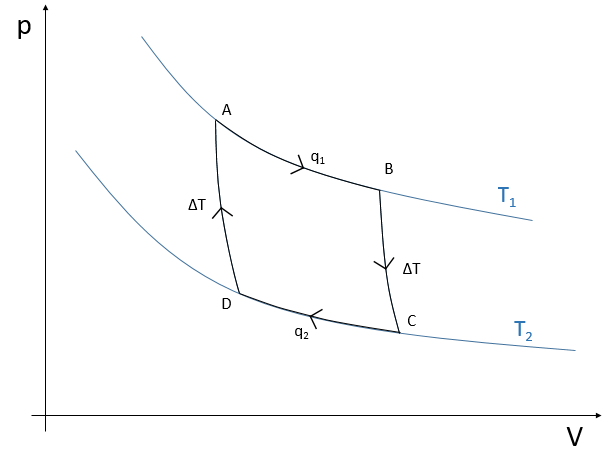
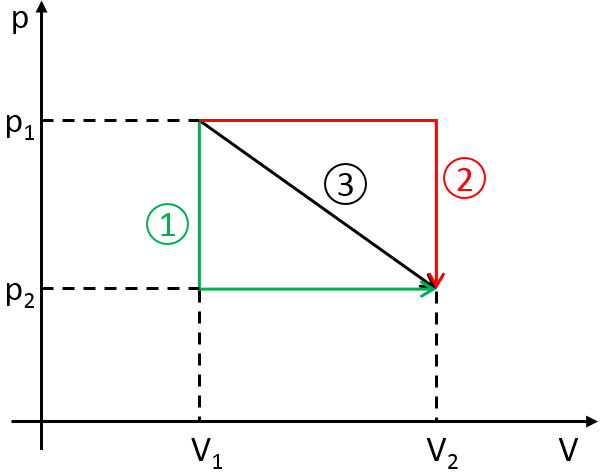
Cycle of Carnot
Nicolas Léonard Sadi Carnot proposed a way to convert thermal energy into work. It is a thermodynamic cycle, i.e. a series of transformations of state leading back to the initial state, composed of two isothermal processes (no temperature variation) and two adiabatic processes (no heat exchange with the environment). All the processes are reversible and the cycle can thus be done in the opposite way, converting work into a difference of temperature.
The setup is made of one reservoir the volume of which can change and that can be in contact with two bodies of temperature T1 and T2, T1 being larger than T2.
First step: isothermal expansion of the gas at T1. The reservoir is in contact with the hot body at T1. Heat q1 is exchanged between the body and the reservoir of gas that expands without variation of temperature. There is thus a variation of entropy ΔS1=q1/T1.
Second step: adiabatic expansion of the gas. During this second step there is no exchange of heat but the gas continue to expand, doing work on the piston and cooling from T1 to T2. The body at T=T1 is not in contact with the reservoir anymore. As there is no exchange of heat, there is no variation of entropy.
Third step: isothermal compression of the gas at T2. The reservoir is now in contact with the second body, at T=T2, causing a transfer of heat q2 while a compression is applied by the piston, keeping the temperature constant. There is thus a variation of entropy ΔS2=q2/T2.
Fourth step: adiabatic compression of the gas. The body at T=T2 is not in contact anymore and there is no possible heat transfer. The gas continue to decrease in volume while its temperature changes from T=T2 to T=T1. At the end of this step, the system is back in the conditions (volume, temperature and pressure) of the initial state.
The cycle can be plotted in the pV phase diagram as shown below:
The efficiency R=W/q1 of the cycle of Carnot would be 100% if all the work W was transformed into heat q. The work here is the difference of heating q1-q2 because ΔE=0=q+W (isolated system, the bodies at T1 and T2 being in the system). As a result,
It is possible to show that the ratio q2/q1 is equal to the ratio T2/T1.
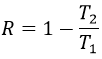
The consequence is that the efficiency is never at 100% except at T2=0K, that we can’t reach on earth. The loss of energy is caused by the production of entropy.
Free energy of Gibbs
For a reaction to occur, we just saw that two factors are important: the enthalpy of reaction (if the reaction is exo or endothermic) and the variation of entropy. The free energy of Gibbs ΔG regroups the two factors in one equation
A reaction is spontaneous if ΔG<0. The entropic term clearly shows that a reaction can be spontaneous at a given temperature but not if the temperature is modified
We can find tables for the values of the standard values of ΔH0 and ΔS0 and subsequently tables of ΔG0 for reactions of formations of molecules. At other temperatures but at 1atm, the relation is
Q is the reactive quotient that we already met previously
For instance, the reactive quotient of this reaction
Is
If ΔG is negative, the reaction goes towards the right, if it is positive, the reactions goes to the left. If ΔG=0, we are at the equilibrium. As a result, we can find a relation connecting the constant of equilibrium K with the free energy of Gibbs:
The chemical potential
The chemical potential μi is the energy of a molecule i that can be used during a reaction or a physical process.
Equation of Gibbs-Duheim:
The last term is thus a variation of energy in the system due to a variation of the quantities of particles in the system, something that we did not take into account before (it will be shown between brackets in the next equations). The relation above comes from the definitions of G and of H:
The partial derivatives of these functions are
We have seen that the internal energy ∂U=∂q+∂W-(∑iNi∂μi) and that ∂S=∂q/T and that ∂W=-p∂V. As a result
The chemical potential is thus the variation of free energy of Gibbs with regard to the variation of concentration of one specific species, keeping the other parameters (p, T and the concentrations of the other species) constant.
We also define the partial molar volume
that is useful for gases. From the law of perfect gases,
That leads us to the expression of the chemical potential for a gas
In solution, the formula is very similar
We know that
So we can find the expression of ΔG as a function of the pressures or of the concentrations of the species:
Yet, this is only true for ideal solutions and gases. Normally, we have to consider the activity a of each molecule
γ is equal to 1 for ideal solutions but may vary if the concentrations increases, representing the increase of interactions between species. However, the activity a of solids is equal to 1.
Third principle
The entropy of a perfect crystal at absolute zero is exactly equal to zero.
The third law provides a reference for the entropy of any pure crystal (and therefore to anything) at any temperature. A perfect and pure crystal is a crystal the arrangement of which is perfectly organised: there is no flaw, the matrix is regular and it is composed by one species. At the absolute zero, i.e. zero Kelvin, the state of the system is at the minimum possible energy. This state is unique as a result of quantum mechanics and it is indeed the case: there is only one way to place the atoms in a perfect crystal. The amount of possible configurations is thus 1, leading to an entropy equal to
If a base state is degenerated, i.e. there are several states of same energy, there are several different possible configurations Ω and the entropy is not equal to 0 but is very close to it. As soon as there is a flaw in the crystal, the amount of possible configurations increases. As a result, the entropy increases. This variation of entropy is synonymous to an variation of energy as told by the second law
The temperature rise dT due to the heat ∂Q is determined by the heat capacity (cp ≈ cV) of the crystal
Consequences of the third law
A first consequence of the third law is that T=0K cannot be reached by any number of finite processes. It is due to the fact that there is only one state of minimum energy. If we tried to change a given parameter in a controlled way so that the energy decreases each time, it would take an infinite number of repetition to reach the absolute zero. It is a bit similar to the problem of the bullet: If at each period of time a bullet moves from half of the necessary distance to reach its target, the target will be approached but never reached. If several states were allowed at T=0K, it would be possible to switch the parameter to obtain one or the other state: one value of the parameter approaches the system from one state and the other parameter approaches the system from the other state. With only one target, we cannot switch from one value of the parameter to the other and reach the final state. We can visualise this like this:
A second consequence is that the heat capacities cp and cV tend to zero when T tends to zero.
Chapter 1 : Thermodynamics – First principle
The thermodynamics is the study of the transfer of energy and especially of heat. It is important to make the distinction between heat (q) and temperature (T). The temperature reflects the motion of particles and is connected to their kinetic energy, but the temperature is no energy. Heat is an energy that exist if there is a difference of temperature, by convention from the hottest to the coldest component. The units of the heat is the units of an energy, i.e. joules J=N.m.
When it comes to transfers of energy, we have to define the system in which we are working. The system is the part of the universe that we are analysing and we distinct it from the environment that is the rest of the universe.
3 kinds of systems can be differentiated
– Isolated system: there is no exchange between the system and the environment
– Closed system: exchanges of energy are possible between the system and the environment
– Open system: exchanges of energy and/or matter are possible between the system and the environment
A system is exothermic if it liberates heat. If it takes heat, the system is endothermic.
The thermodynamics is governed by 3 major principles.
First principle
Conservation of the energy: The energy of the universe is constant.
It means that a process occurring in an isolated system doesn’t involve any variation of energy. If exchanges of energy are allowed with the environment, i.e. in closed systems, the intern variation of energy in a system is composed by the heat q and the work W to make the process.
If the system also allows exchanges of matter, a term dEm representing the energy of the flow of matter is added.
The variation of energy is a state function. It means that this function does not depends on which way the system reached this point, but only on its initial and final state. W and q are not state functions and depend on the way the system evolves during the process.
The work has a negative value if it is made by the system. For instance, imagine a volume in which a gas is stored.
To compress the gas, the environment has to apply a force on the piston. W is thus positive in this case. If the piston is free of movement, the gas in the volume applies a pressure on the piston to increase the volume of the system. In this case W<0.
The work is an energy, so it is basically a force multiplied by a distance. If we consider the dilatation of a perfect gas the work would be
To move from a state (p1,V1) to (p2,V2) several paths can be taken.
Those ways are equivalent in the term of variation of energy because the energy is a state function: the final state and the initial states are characterised by an energy that does not depend on how they were obtained. Yet, the work and heat are different for each path.
Indeed, on the path 1, W=-p1(V2-V1). On the path 2, the work is W=-p2(V2-V1). As p2<p1, it means that more work is required on the path 1 and that there is a larger production of heat on the path 2. On the path 3, the volume and the pressure vary simultaneously. We use the law of perfect gas to determine the work in this case. Path 3 is in fact an isothermal curve, where q=0.
Now, let’s talk about heat. In previous chapters, we discussed about the heat capacity. It is the energy required to increase the temperature of the substrate by one kelvin/degree. We distinguish the heat capacity at constant pressure Cp and at constant volume CV.
Note that we used partial derivatives ∂/∂T instead of derivatives d/dT. A partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant.
H is the enthalpy of a state and ΔH is the variation of enthalpy of the process (that can be a reaction or a transition of phase for instance) at a constant pressure. ΔH is thus equivalent to qp, the subscript p indicating that it is the heat at p=cst.
The equation for the enthalpy is
For perfect gases, pV=nRT, so
Given that Cp= ∂H/∂T we find a relation between Cp and CV for perfect gases
For solids and liquids, the variation of volume is negligible and Cp»CV.
Calorimetry
An enthalpy of reaction ΔH° is associated with each reaction.
The ° indicates that this value is the enthalpy found for one mole of reactant, at 1atm. The enthalpy of a reaction can be measured experimentally by calorimetry. During calorimetry, a reaction is made in an isolated system (no exchanges with the environment). The variation of temperature in the system is measured and from this measure we can deduct the heat of reaction. For instance, the neutralisation of HCl by NaOH is exothermic (ΔH°<0), meaning that this reaction generates heat. It is thus possible to measure a variation of temperature ΔT during the reaction. To do so, we use an isothermal and closed recipient in which the reactants are initially separated. The temperature in the system can be read on a thermometer. The temperature is not directly taken in the reactive solution. Usually, the reaction takes place in a recipient (called the calorimetric bomb) that is surrounded by water. The whole setup is in the isothermal recipient. The variation of temperature is measured in the water. When the reaction takes place, the elevation of temperature is recorded in function of the used amount of NaOH. With the adapted setting, we can measure qp (p=cst) or qV (V=cst).
If the pressure is kept constant, the variation of temperature ΔT is proportional to qp.
As we consider a liquid phase, qp»qV.
CV can also be determined experimentally: A given heating is applied in the solution through an electric resistance.
With V the tension and R the resistance. The variation of temperature ΔT due to this heating depends on the heat capacity of the liquid.
So if we know the applied tension and the resistance, the measure of the variation of the temperature gives us the value of Cv.
Law of Hess
The energy and the enthalpy are state functions, i.e. their value does not change in function of the path/process and are only a function of the state of the system. It means that if we perform a cycle of transformations, obtaining at the end our initial compounds, the sum of the variations of enthalpy of the processes of the cycle is equal to 0kJ/mol. Note that the absolute value of the enthalpy of a body cannot be determined. Only variations of enthalpy can be determined. It means that we can determine the value of enthalpies with regard to a given process and thus that the enthalpy of formation of a molecule is determined in comparison with other reactions.
By convention, the enthalpy of formation of simple bodies composed of one single element (for instance O2, H2,Na,etc but H2O not because there are two different atoms in the molecule) in their standard state equals 0kJ/mol. The standard state is the most stable state of a body at 25°C and 1 atm. In the nature, some elements can be found in several states but the body in its normal state at 25°C and 1 atm alone has a ΔfH°=0kJ/mol. For instance, the carbon can be found as graphite and as diamond.
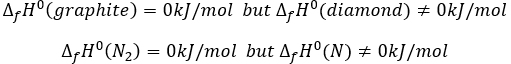
We say that the graphite and the diamond are two allotropes of carbon. The atoms are bond together differently in those two solids. Between them, the standard state of the carbon is the graphite because the diamond is not formed in this range of pressure and temperature. Technically, the notion of standart state depends on the temperature and pressure, and the diamond will be the standard state of carbon for very high pressures but we commonly use the “standart state” term for the normal conditions of temperature and pressure.
For molecules that are not in their standard form, the enthalpy of formation is the enthalpy of the reaction producing the molecule from the elements in their standard state that compose it.
The enthalpy of this reaction is thus the enthalpy of formation of the carbon dioxide CO2: it is the reaction that generates carbon dioxide from the elements in their standard state that compose CO2.
This reaction is the reverse of the formation of the methane CH4. The enthalpy of reaction is simply minus the enthalpy of formation ΔrH°=-ΔfH°.
The enthalpy of this reaction is twice the enthalpy of formation of the water because we form two moles of water with this reaction. The enthalpy of reaction is given in kJ by mole of product
If we combine those three reactions, we obtain the cycle of Hess. The enthalpy of this final equation is the sum of the enthalpies of formation of the three sub-reactions:
We can sum up the enthalpies of the sub-reactions to obtain the enthalpy of reaction of formation of CO2 and H2O from CH4 and O2.
In a general way, the enthalpy of a reaction is the sum of the enthalpies of formation of the products minus the enthalpies of formation of the reactants, each one multiplied by its stoichiometric coefficients.
We clearly see here that those two expressions are identical
Don’t forget that the enthalpy is a state function but depends on the temperature and that a reaction can be favoured by a variation of temperature.
At a constant pressure, the enthalpy can thus vary if there is a variation of temperature
A change of state will also increase the enthalpy of reaction.
If we want to change ice into vapour, i.e. sublimate ice, at a constant pressure=1atm,
the enthalpy will be
The triple point is a particular point where ice, vapour and water coexist and where
From that point, we can find the enthalpy of one phase transition from the other two.
Energy of liaisons
We have seen that we can find the enthalpy of reactions from the enthalpies of formations of each participant of the reaction. There should thus be reactions that allow us to determine the energy of chemical bonds. For instance, the reaction
is basically the scission of 4 C-H bonds. Nothing else has been done during this reaction. We can determine the enthalpy of the reaction ΔrH0 from the enthalpy of formation of CH4, C and H. We have seen earlier the inverse of the reaction of formation of the methane
From that reaction, we still need to dissociate the molecules of H2 and to sublimate the graphite into a gas.
As there are 4 C-H bonds that have been broken, each bond has an energy of 419kJ/mol.
Fuels
The thermochemistry is a vast domain of the chemistry that finds applications in fuels for example. We can determine the energy of liaisons during the combustion of molecules composing the fuel, exactly the same way as we did for the liaison C-H. The hydrazine N2H4 is a nitrogen molecule used as fuel for space propellers.
Most of the nitrogen compounds have a positive enthalpy of formation, meaning that we need to spend energy to generate them. It also means that they will easily break to form N2 and H2O, generating a lot of energy. An exception is NH3. What is the energy of the reaction? O2 and N2 are in their standard form, meaning that their ΔfH0=0kJ/mol. The enthalpy of reaction is thus
This reaction generates heat because the energy of the formed liaisons is greater than the energy of the broken liaisons. We broke 4 N-H bonds to form 4 O-H and the N-N bond became a triple liaison N≡N. The O-H and N≡N liaisons represent respectively 460kJ/mol and 941kJ/mol.
Because of all the energy that has been generated by the reaction, the water changes of phase and becomes gaseous. The propulsion of the space shuttle is not only the result of the energy but comes from the expansion of the gas: from one mole of gas we make 3 moles of gas. The gas expand very quickly because of the heat (pV=nRT), generating the explosion in the propeller.