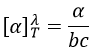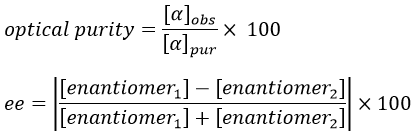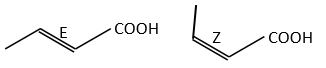Editor’s note: It is a good exercise to determine the configuration (R or S) of each chiral centre presented in this course.
Some molecules have the same composition in terms of atoms but differ by their placement. Those molecules are called conformers (of configuration). Amongst them we distinguish enantiomers and diastereoisomers. The distinction was already explained in a previous section and we will explain it here too. Despite one slight difference of arrangement, the activity of two enantiomers can often differ signifficantly, especially in biology where the damages can be important. Pharmaceutical industries have to separate the enantiomers in the medecines or prove that the other enantiomer is truely inactive. Separation methods exist to isolate one of the enantiomer but it is one more step in the process and there is still 50% of product that is simply lost. For that reason, the field of asymmetric synthesis developped quickly in the current of the 1980’s.
Examples of problems due to the enantiomer
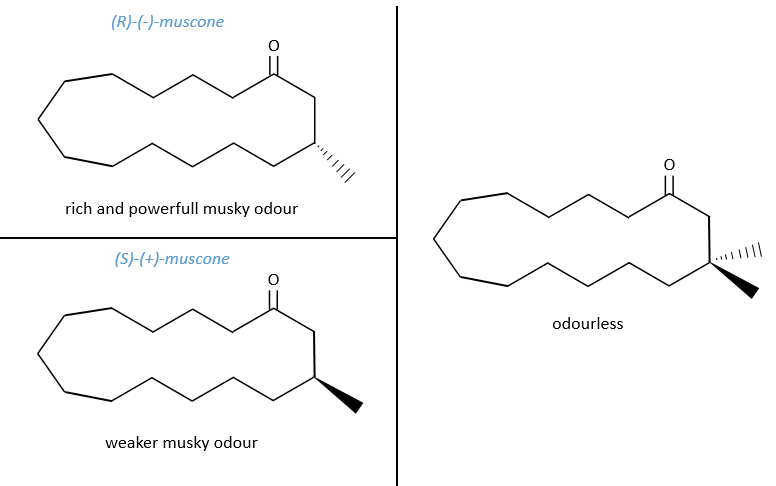
A melange of enantiomers can be less active for antagonism reasons: one enantiomer blocks the activity of the other enantiomer. For instance, the R pheromone of japanese cockroaches becomes totally inactive if the isomer S is present (the notion of R,S, (+) and (-) will be explained soon), even in a proportion of 1%. The S isomer can fix itself on the same receptor than the R isomer but it is inactive. Once it is on the receptor is doesn’t leave, making the R isomer inactive.
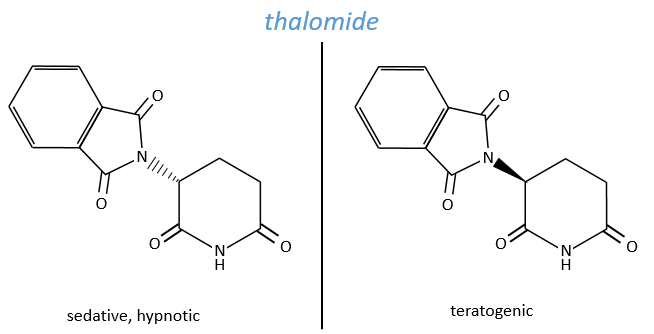
The use of a melange can be dramatic. Thalidomide is a medecine that treat the symptoms of sleeping troubles and of depression. The molecule is active even in presence of its isomer but the isomer causes damages to the phoetus of pregnant women. Disformed babies were born because the enantiomers were not separated at this time.
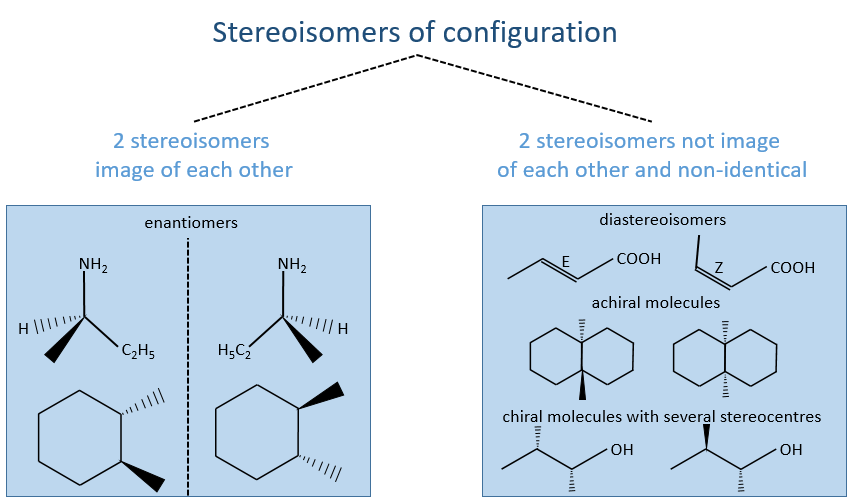
On the figures above, we use three types of lines to represent liaisons:
- a full line indicates either that the liaison is in the plane of the sheet or that its direction outside this plane has no interest,
- black triangles mean that the liaison goes out from the plane of the sheet (point side of the triangle) towards the reader (base of the triangle). It can be seen as a full line we see closer and closer,
- parallels lines in the shape of a triangle is the opposite of one black triangle: the liaison goes from the plane of the sheet (small side) to away from the reader (large side).
Another example is the penicillamine. One isomer is an antidote to poisoning by Pb, Au or Hg. The enantiomer can make you blind.
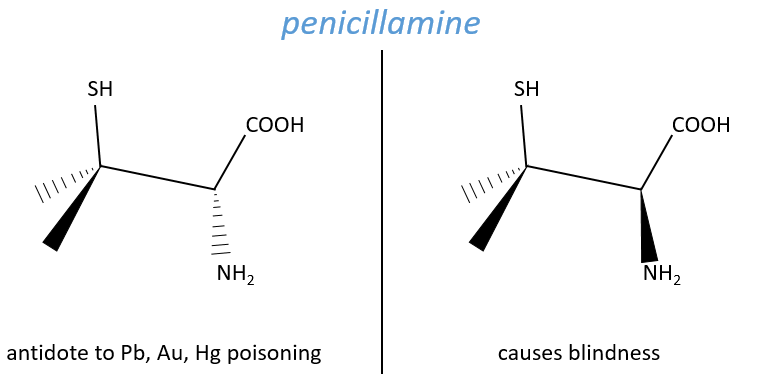
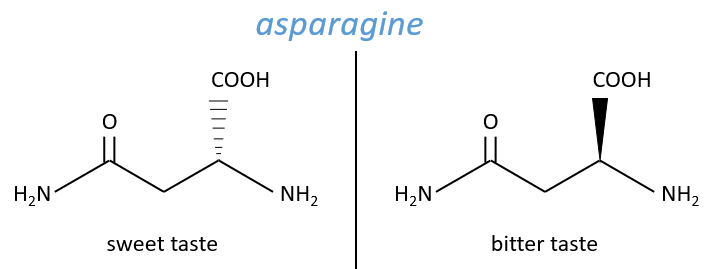
No need to say that it is better to avoid any melange of the two enantiomers. Eniantiomers can also show big difference in taste or smell because they will activate different receptors in our nose/on our tongue.
Reminder on the stereoisomery
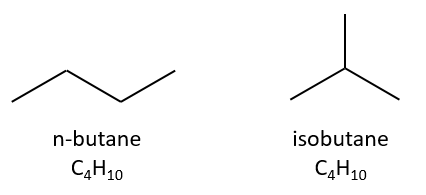
Isomers are compounds of same composition but with a different structure. Isomers of constitution have not the same arrangement of atoms. A simple example is the n-butane and the isobutane.
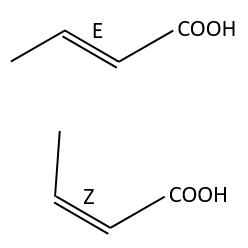
Amongst the isomers, we distinguish stereoisomers. In stereoisomers, the sequence of atoms is identical but the spacial arrangement of the atoms is different. Stereoisomers of configuration can be separated and isolated. To pass from one stereoisomer of configuration to another one, one liaison has to be broken. For instance, the configuration around a C=C liaison can be Z or E, but we have to break the π liaison to go from one to the otherone.
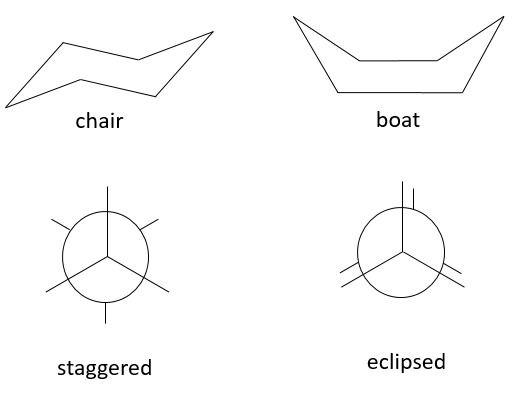
Stereoisomers of conformation, or conformers, are different arrangements of the same molecule obtained by the rotation of one (or more) σ liaison. There is a barrier of energy for this rotation, which can be huge if the rotation is made difficult by the presence of a sterically hindred substituent. Moreover the rotation depends on the temperature. An simple example is the chair-boat conformers of the hexane.
The chair conformation is favoured by 6kCal/mol because all the substituents are in staggered position while they are all in eclipsed position in the boat conformer, leading to a bigger sterical hindrance. There is an equilibrium between the two conformers which is completely displaced towards the chair conformation at ambiant conformation. If we decrease the temperature we can observe both conformers and even separate them. The barrier of energy depends on the substituents of the hexane and the compound is more stable when big substituents are on an equatorial spot because the steric hindrance is smaller there. On the boat conformation, the steric hindrance is always more important because all positions are eclipsed.
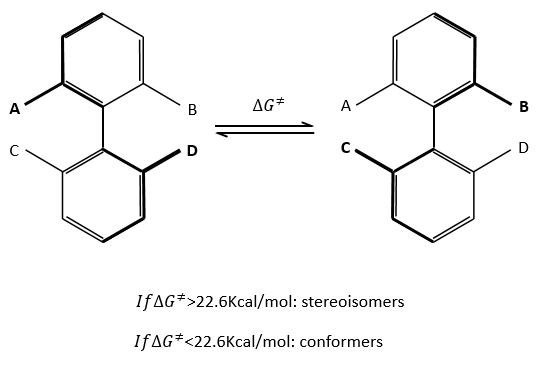
Sometimes the rotation of one liaison is so much hindered that the life time of the isomer is long enough to be considered as a stereoisomer instead of as a conformer. As a general rule, we say that we are in presence of conformers if ∆G¹<22.6kCal/mol. If it is larger, then we are in presence of stereoisomers (atropoisomers: denial by steric hindrance). This value corresponds to a life-time of approximatively 1 hour at 25°C.
Binaftines are composed of two benzenes bound by one σ liaison. If there is no substituent on the aromatic cycles, the molecule is plane. The liaison between the cycles is not completely one σ liaison as all the π liaisons are conjugated. If there is one or more substituent on A, B, C or D, the steric hindrance doesn’t allow the planarity of the molecule and it becomes very difficult for the σ liaison to make a complete rotation. For instance, the binaftol cannot turn at ambiant temperature.
Chirality
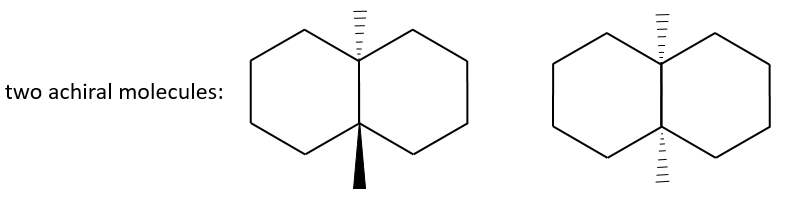
The chirality is the property of an object not to be superimposable to its image in a mirror. The usual example of chiral objects is our hands. The left hand is the mirror image of our right hand but we cannot superimpose them. Indeed, if our palms are in front of us, the fingers are not at the same place. For instance thumbs are not at the same side of the hand. Even if we rotate one hand by 180°, fingers are at the same place but not in the same direction. The word itself, chirality, is derived from the greek word for hand. As a general rule, if a molecule has no plane or centre of symmetry, this molecule is chiral. Yet, there can be an axis of symmetry in achiral molecules.
The stereogenic unity responsible for the chirality of the molecule can be
- an atom,
- an axis
- a plane
- the helicity of the molecule
There are thus 4 main types of chiral molecules.
Amongst the stereoisomers of configuration, we distinguish the enantiomers that are chiral and the diastereoisomers that are not chiral and not identical.
Enantiomery
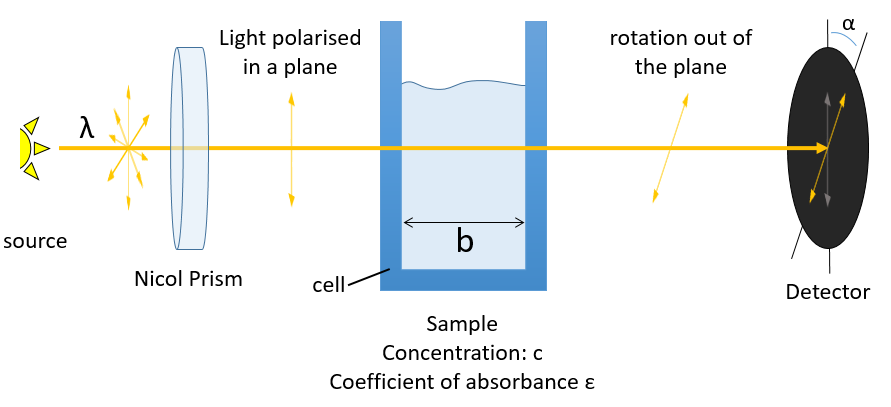
The distances between the atoms are identical in enantiomers. As a result, the chemical and physical properties of enantiomers are identical as long as there is no external chiral influence. A particular property of chiral molecules is their optical activity or rotatory power [α]. A chiral substance crossed by a polarised light induces a rotation of the plane of polarisation of the light in one direction.
The direction in which the light is deflected depends on the enantiomer. For instance the 1,1-aminophenylethane has two enantiomers the optical activity of which is [α]D=39 and [α]D=-39 if illuminated by sodium at 20°C (the D indicates these experimental conditions). The specific activity of one enantiomer is given by
where λ is the wavelenght of the polarised light, T the temperature, α the observed angle of rotation, b the length of the cell containing the substance and c the concentration of the solution. The cell in itself has to have no optical activity.
If the value is negative, the compound is levogyre (noted l or (-)) and if the value is positive, the compound is dextrogyre (d or (+)). In the case of the 1,1-aminophenylethane, the R enantiomer is dextrogyre with an optical activity of [α]D=+39 and the S enantiomer is levogyre [α]D=-39). Unfortunatly, there is no correlation between the fact that the enantiomer is R/S and levogyre/dextrogyre.
If the solution is composed of a 50:50 racemic melange of two enantiomers, the light is not deviated and [α]=0. In fact the light is deviated at the miscroscopic scale but in average there is no deviation at the detector because the rotatory powers of the enantiomers counterbalance each other. We define the optical purity (also called the enantiomeric excess ee) as
Stereogenic centres
1) centre of chirality
An asymmetric carbon (or any other tetravalent atom) on which there are 4 different substituents is a centre of chirality. The absolute configuration is the real disposition of the atoms around the atom of carbon. The carbon is S or R, what can be determined with the rule of Cahn, Ingold and Prelog (CIP)(there is a second method that can be used if you prefer it).
The first thing to do is to find the atomic number of the atoms bound to the assymetric carbon (consider zero for a lone pair). If two substituents have the same atomic number, we look at their substituents (starting with the highest atomic numbers), etc.
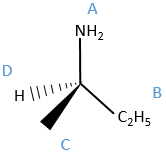
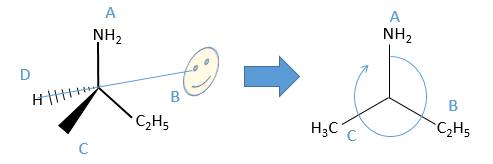
We can name them A, B, C and D starting by the highest atomic number. In the example above, the substituent A is NH2 because N has a higher mass than C or H, the other atoms directly bounds to the assymetric carbon. To determine B, there are two substituents bound via one carbon and one via one hydrogen. As the mass of C is larger than the one of H, we look at the substituents of the carbons, in the methyl group, there are 3H and in the ethyl there is two H and one C, so the ethyl group primes over the methyl group. We have thus A=NH2, B=C2H5, C=CH3 and D=H. The next step is to place the liaison between the carbon and the substituent of lowest atomic number in our axis of sight. The carbon is between us and the substituent D. The three other substituents are pointing towards us and are approximatively in the plane of the papersheet. We can draw the liaisons between them and the carbon.
If A, D and C are in the horlogic order, the carbon is R. Otherwise it is S.
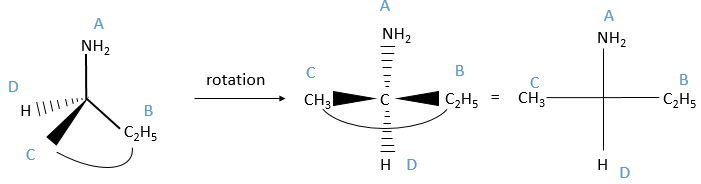
The second method uses the representation of Fisher on which the four liaisons are on the same plane. In reality it is not the case: to obtain this representation, imagine that you hold any two substituents with your thumb and your forefinger (for instance B and C).
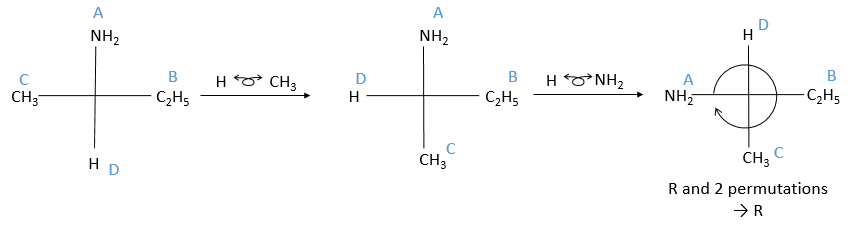
Then you rotate the molecule to form an horizontal plane with the assymetric carbon, pointing in your direction. The other two liaisons are vertical and pointing away from you. The goal now is to place the substituent of lowest priority at the top of the representation. To do that, we can swap the places of the substituents if the are direct neighbours. It is almost as simple as that: for each permutation made, the configuration also changes from R to S or vice versa. As a result, if we made two permutations, the configuration remains the same (R→S→R). We apply this at the end, but remember the number of permutations made.
When the lowest priority subsitutent is at the top, we ignore it and we determine the “observed configuration” the same way than in the previous method: if they are in the horlogic order, then it is R, otherwise it is S. To obtain the real configuration from the observed configuration we just determined, we swap between R and S for each permutation made.
You may want to place the substituents in the horlogic order with permutation in all cases. You can do it if it helps you, but don’t forget that each permutation changes the configuration.
2) Axis of chirality
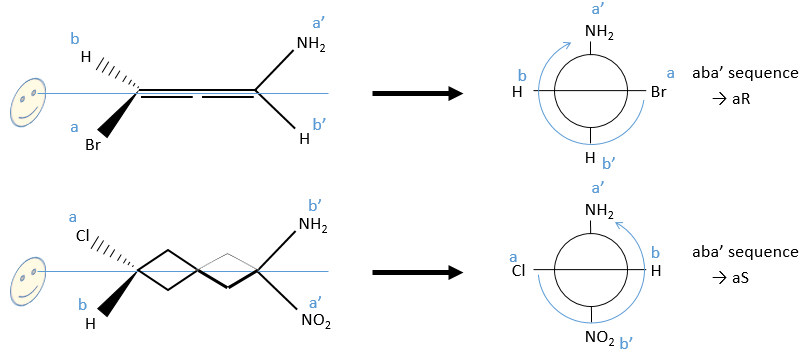
A similar method is followed. The difference is that we separate the substituents by their side of the axis ‘noted with and without prime). We will use the projection of Newton following the axis of chirality. The substituents at the front (the side we put in front does not matter) are noted a and b in function of their atomic number and the ones at the back a’ and b’. Next we check if aba’ is in the horlogic order (aR) or not (aS).
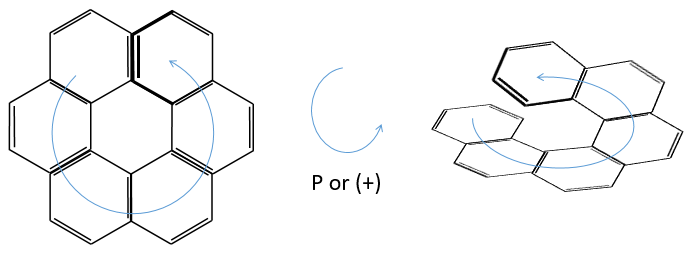
3) Helicoidal chirality
If the helix goes from the top to the bottom in the horlogic order, then it is noted P or (+). Otherwise it is M or (-).
Diastereoisomery
Two stereoisomers that are not enantiomers are diastereoisomers. It can be the case if there are several stereogenic centres in the molecule.
Two stereogenic centres
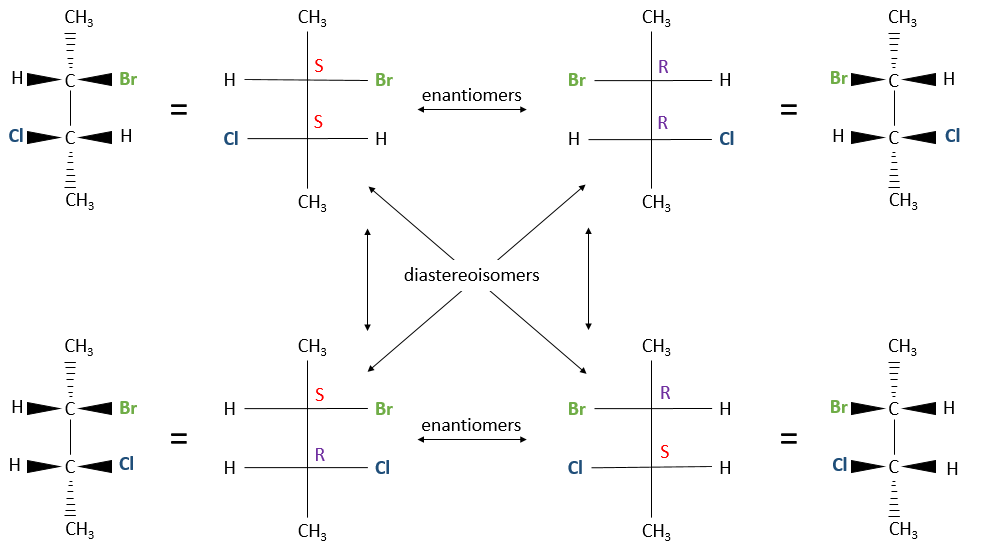
When the configurations are identical (RR or SS) are called like and when they are different (RS or SR), called unlike. Diastereoisomers haven’t the same chemical and physical properties because the interatomic distances are different. In the previous figure for instance, the distance between Br and Cl is different for the RS and the RR configurations. It is thus possible to separate them with usual techniques.
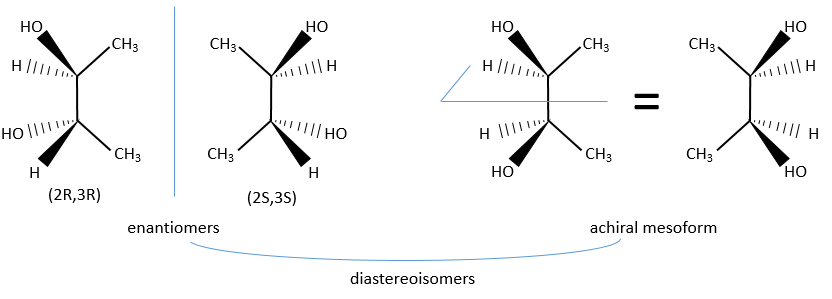
In the case of two asymmetric carbons, there is one enantiomer by configuration and two diastereoisomers. Yet the two diastereoisomers are sometimes one unique configuration that we call the meso form. For instance there is only one diastereoisomer for the enantiomers (2R,3R) and (2S,3S) of the 2,3-butanediol.
The reason here is a plane of symmetry between the carbon 2 and 3 of the butanediol.
Double liaisons
The presence of a double liaison entraves the rotation of the liaison. If there is at least one different substituent on each of the two carbons, there are then two stereoisomers that are called Z is the substituents of largest atomic number are in cis position, i.e. on the same side of the double liaison, and E if the substituents are in trans position, i.e. on the opposite side of the double liaison.
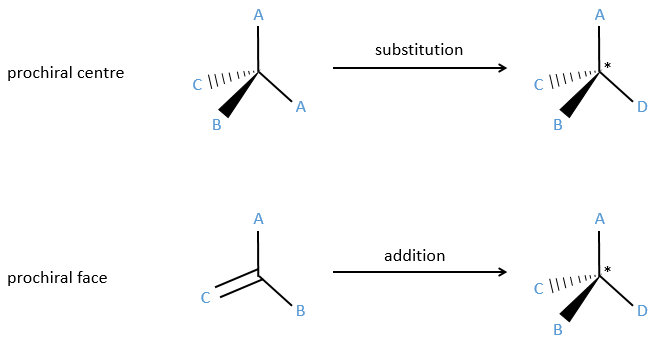
Prochirality
An achiral molecule is said to be prochiral if when we replace one of the substituent by a different one it becomes chiral. It implies that the two ligands that were apparently indiscernable are not equivalent.
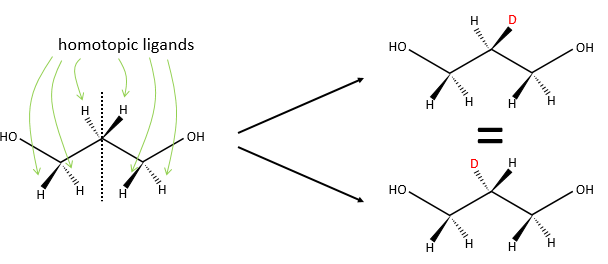
Homotopy and heterotopy
In a not-prochiral molecule, the substituents that are identicals and are related one each other by a rotation around an axis of symmetry of order n are said to be homotopic or equivalent. If we replace one of those equivalent substituent by a different one, the product is identical than if we replaced the other homotopic substituent.
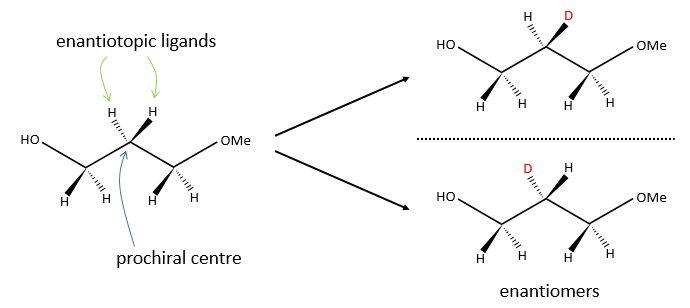
In opposition, we talk about eniantiotopic ligands (or substituents) if there was a centre of prochirality. The two ligands are identical and are the result of a symmetry of each other but if we replace one of them by another substituent, then we don’t get the same molecule than if we replaced the other eniantiotopic ligand.
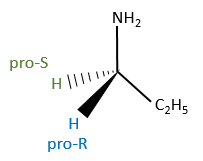
To name these molecules, we use the CIP method and we randomly give the priority to one of the eniantiotopic ligand. This ligand is pro-R if the CIP method gives R and pro-S if the CIP method gives S. The second eniantiotopic ligand has the opposite name.
Two eniantiotopic ligands can’t be distinguished by usual physical and chemical methods, by RMN for instance. However, a chiral reactant like an enzyme can make the difference between the pro-R and pro-S ligands.
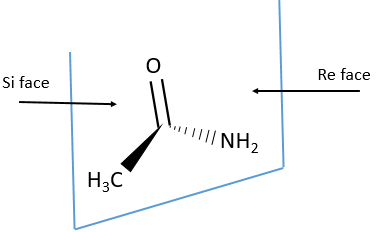
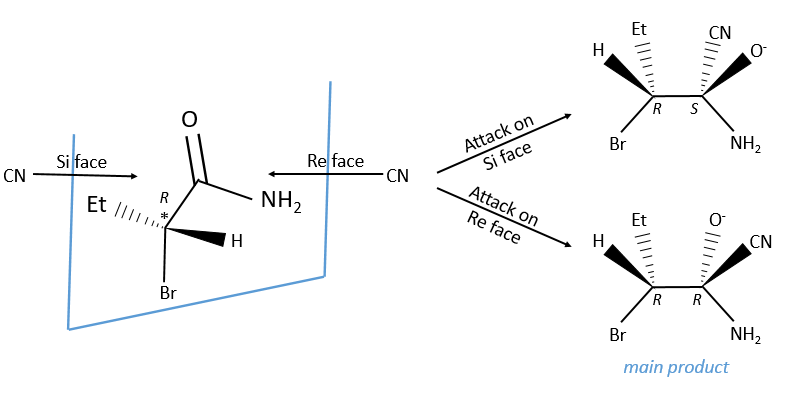
Eniantiotopic faces
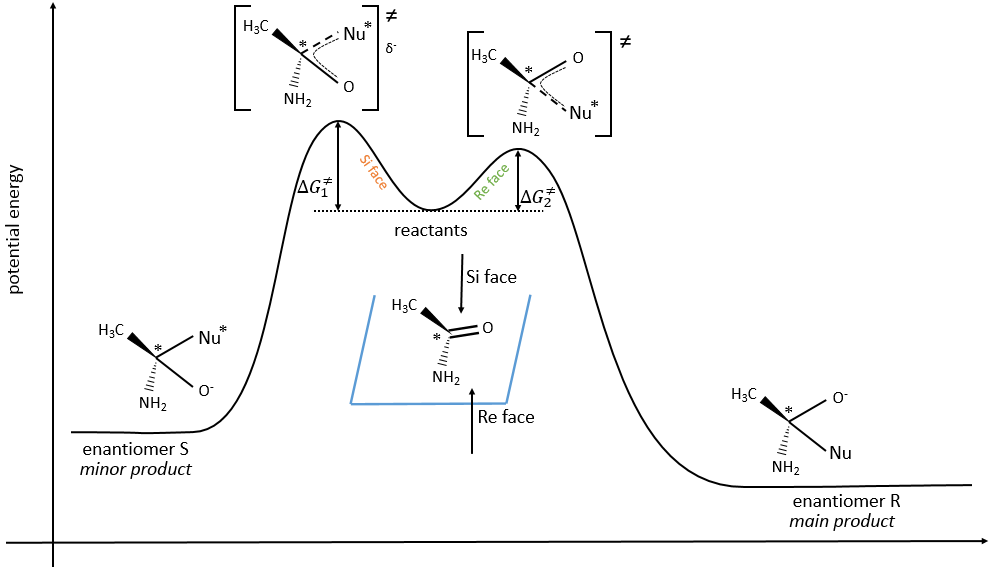
In addition to eniantiotopic ligands, we also talk about eniantiotopic faces if a double liason is bound to a prochiral centre. The face of the plane on which the substituents are in the horlogic order is called face re and the other face is called face si.
The probabilities to attack by the Re or by the Si face are equal if the nucleophilic species is achiral. In this case we obtain a 50/50 racemic melange of the enantiomers R and S. If the nucleophile is chiral, then the reactions on the Re and Si faces have different speeds. The reaction is diastereoselective.
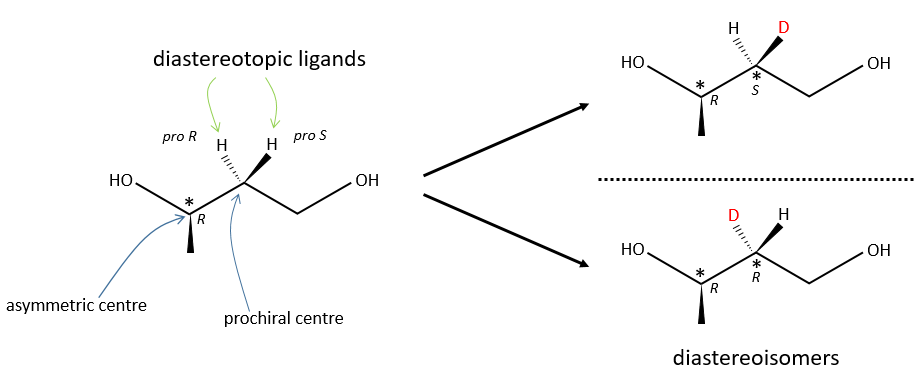
Diastereotopic ligands and faces
A prochiral centre can be near an asymmetric carbon. Two identical ligands of the prochiral centre are then not equivalent because they are not at the same distance from some groups of the asymmetric carbon. The replacement of one of the ligands or of the other leads to two diastereoisomers.
Achiral reactants can make the distinction between diastereotopic faces, one being usually more hindred than the other one. It leads to one product more formed than the other one. The products are diastereoisomers.
The less hindred side is usually favoured (model of Felkin).
Racemisation
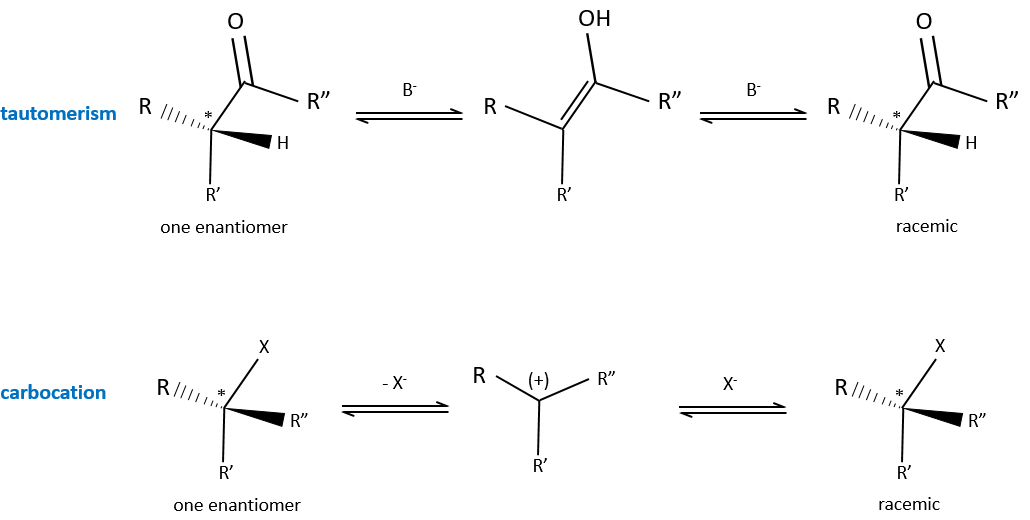
It is the passage from one active optical body to the corresponding racemic melange. The racemisation can be due to time, heat or chemicals. In a general way, the cleavage of one liaison is involved and a carbon in the intermediate species possesses one sp2 carbon.
An example of racemisation is the enol-ketone tautomery. Starting from a solution made of one single enantiomer of a ketone, the other enantiomer will appear if there is a trace of a base in the solution because of the passage by the enol form. Under the sp2 form, the carbon is plane and there is thus no more S or R configuration. Both enantiomers can be formed from the enol.
Another example is the passage from one enantiomer to the other by the formation of a carbocation.
Epimerisation
Epimers are diastereoisomers with several stereogenic centres that differ only by the configuration of one of those centres. The epimerisation is the passage from one epimer to the other one.