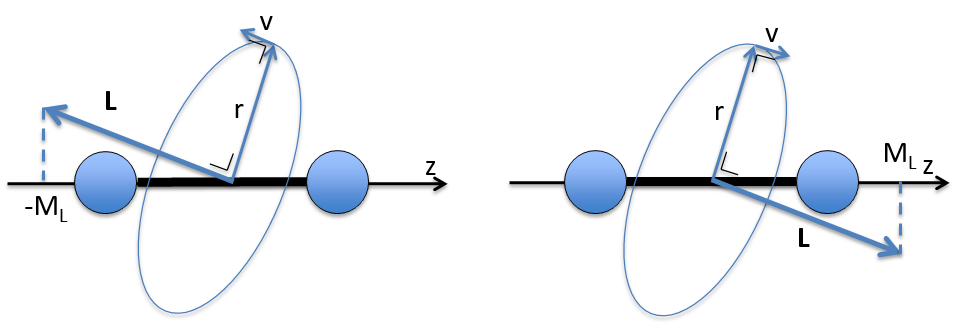
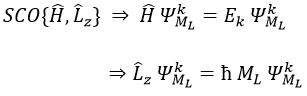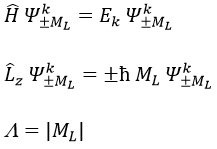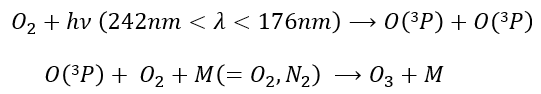The electrons revolving on an orbital generate an angular moment.
ML is the quantic number associated to the projection of L on the internuclear axis.
The projection is degenerated because it can either be in the positive values of the z axis or in the negative ones. The projection of L can thus give ML or –ML. We can define a new quantic number L=∣ML∣.
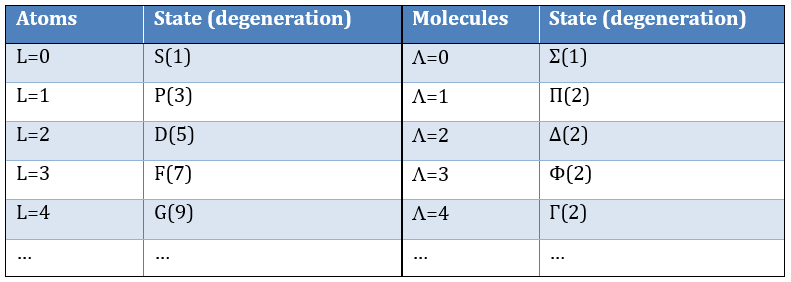
The fact that there are two projections explains the dimension 2 or the orbitals π, δ, … of linear molecules. The length of the projection of L grow if L gets larger but the degeneration is always 2. The only exception is Σ for which ML=0. In the atoms we had the possibility to choose the orientation but we cannot do that with molecules.
As a result, the operator σv doesn’t commute with Lz:
except for L=0 that gives the states Σ+ and Σ –. This distinction + or – is not present for the states Π, Δ, …
The fact that σv doesn’t commute with Lz induces the degeneration of the states.
The inversion operator Î still commutes with Ĥ, Lz and σv in the case of centrosymmetric molecules.
As a resume, the operator σv is separated from the other operators of the CSCO of linear molecules because it does not commute with Lz anymore.
Application to H2
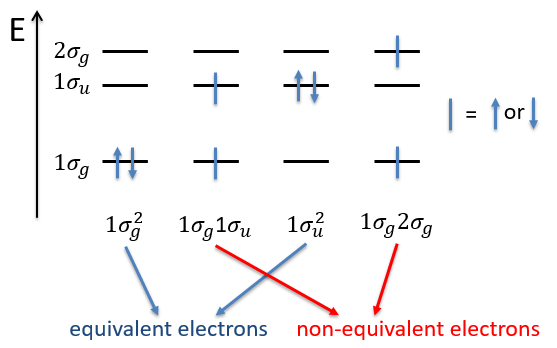
Let’s take a look at the possible electronic configurations of the molecule H2.
The unexcited state of H2 has two equivalent electrons on the ground orbital 1σg:
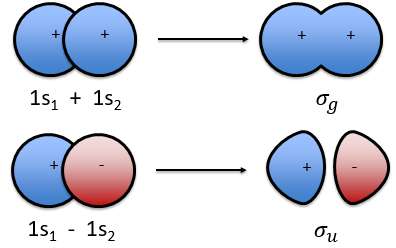
This state is binding: between the nuclei, the probability of presence of electrons is positive. In antibonding states, there are some points between the nuclei where the probability to find electrons is zero.
The first excited state is the configuration 1σg1σu. In this configuration the electrons are not equivalents and the degree of degeneration is 4 (2×2):
To determine the states, we take the emergent (ML=0,MS=1). It corresponds to the triplet 3Σ u + (the pairs (0,1), (0,0) and (0,-1)). The second emergent (0,0) corresponds to the singlet state 1Σ u +(the pair (0,0)).
To determine the energy of the states, we proceed as for the atoms with the determinants of Slater
In the case of an emergent such as (0,1) we have a proper function and thus the energy can be determined. From this function we find the other functions with operators of rise/descent S+ and S– and with the principle of orthogonality we find the energy of the singlet state.
The dashed curves are correspond to unstable states because there is no minimum of energy: the atoms are get more stable as they get away one from each other.
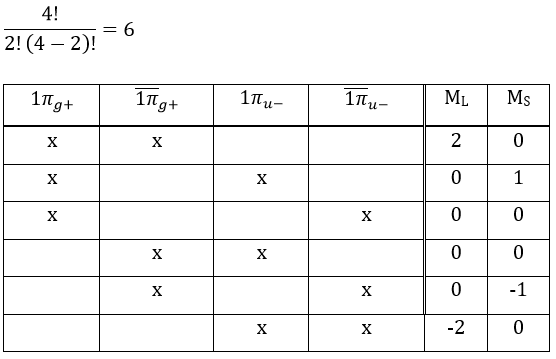
Application to O2
The same method can be applied to O2. Its fundamental configuration is
As usual, we only consider the highest occupied molecular orbitals (HOMO). Those are the 2 1πg orbitals with 2 electrons to place, represented above by the circles: they can be on the same orbital or separated. There is thus a degeneration of 6:
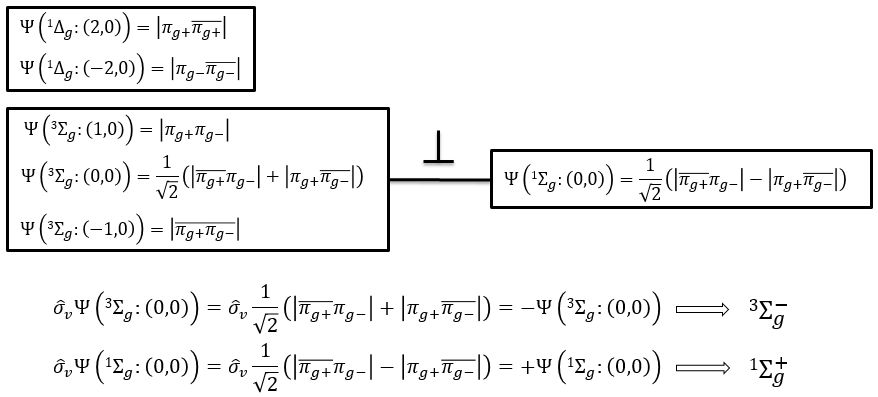
The first emergent is (2,0). That corresponds to the group 1Δg. Remember that the degeneration for linear molecules is 2 except for ML=0. In the atomic case, we had a degeneration of 2L+1 (i.e. ML, ML-1, …, 0, …, –ML-1, -ML) but here we just have ML and –ML. The next emergent is (0,1), a triplet 3Σg. Finally there is a singlet 1Σg. To know if it is Σ+ or Σ–, we have to apply the operator σv. In this case we have 3Σg– and 1Σg+.
Ozone is obtained by the excitation of one molecule of O2 at its fundamental state into two oxygen atoms in the 3P state. In this state, they react with another molecule of O2 and a catalyst to produce the ozone.