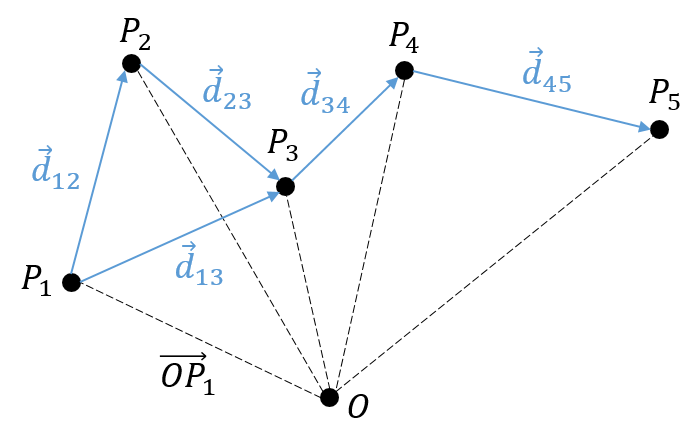
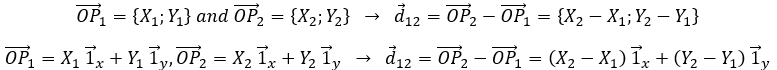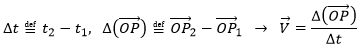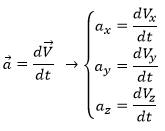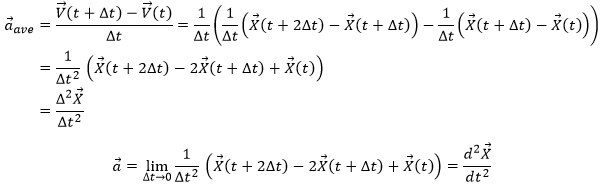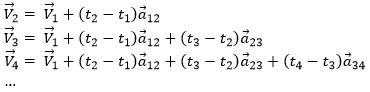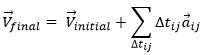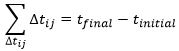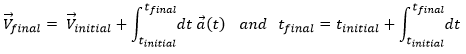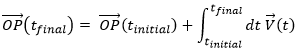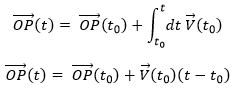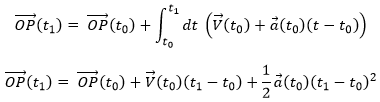There is a motion if the vector ![]() changes over time. We can thus note this dependence
changes over time. We can thus note this dependence ![]() . The variation of position is thus the motion. Noting the position of the object P1, P2, P3, … at consecutive times t1, t2, t3, … , we can introduce the displacement vector
. The variation of position is thus the motion. Noting the position of the object P1, P2, P3, … at consecutive times t1, t2, t3, … , we can introduce the displacement vector ![]() as the vector
as the vector ![]() , and if the objects continues to move,
, and if the objects continues to move, ![]() , etc.
, etc.
Several observations can be made at this point:
- it may look obvious, but there is always one position more than there are displacements. As a result, it is impossible to determine the position of the object from its displacements alone. We will need at least one of its positions.
We introduced here the addition operator + on vectors. In the Cartesian system, it is easy to see that the addition and the subtraction operators are simply the mathematical + and – operators applied on the numbers corresponding to the coordinates.
The average speed
Now that the displacements are defined, we can consider that it doesn’t take the same time to make the displacement between P1 and P5 directly or with the intermediate steps. The average speed is defined as the displacement by unit of time. At the initial time t1, the object was at the position P1 defined by the position vector . At the time t2, the particle has moved from this position to the position P2, defined by the position vector . The average speed between these two positions is thus the displacement of the object divided by the interval of time t2-t1.
The speed is said to be average because it depends upon the two chosen positions. One common notation in mathematics is to write differences of two values by the sign Δ. We can thus write
That we can also write, with the explicit dependence over the time:
The instantaneous speed
One concept is now to get rid of the two positions to define an instantaneous speed, associated to a given position and a given time. To do so, we will bring the second point closer from the first and see what happens. We can’t only chose one point because the division by zero is not allowed. However, if this ratio continues to exist when the two points are almost identical, then the instantaneous speed is this value.
It is also the definition of the derivative of the position with regards to the time, calculated at t1. The limit towards zero of Δ will be noted d to obtain the notation corresponding to the usual derivative.
To indicate at which time we look for the speed, we use the notation
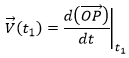
Each component of the speed is given by the derivative of the corresponding component of the position with regards to the time.
The acceleration
The same way we defined the speed as the variation of the position over time, the acceleration a is the variation of speed over time. We define an average acceleration as
and the instantaneous acceleration as the derivative of the speed vector with regards to the time.
The acceleration can be obtained directly from the position by taking its second derivative. We introduce the notations
Note the difference of position of the square exponent: it is the derivative d/dt that is taken twice, not the object of the derivative. It is more evident if we use the definition of the derivative explicitly:
As the acceleration is a difference of speed, there is thus always one acceleration less than there are speeds. From a speed at a time t1, on can determine the speed at a time t2 if we are given the acceleration during the interval of time.
From point to point, we can thus determine the speed:
We can generalise this as
Obviously, the sum of the intervals of times equals the elapsed time:
At the limit of the discrete time jumps, the sum becomes an integration
From the speed to the position
We can apply the same method on the speed to obtain the position:
Let insist on the physical meaning of this:
- the integration∫ is a sum,
- this sum is always made on a product,
- this product always contain an infinitesimal difference (here the time dt) and one finite quantity (here the speed V(t)),
- the sum ∫ is defined between a point of beginning and a point of end.
The uniform rectilinear motion
A uniform rectilinear motion (URM) is obtained when the speed of the object doesn’t depend upon time. The speed is thus constant and is defined at the initial time t0.
As the speed is constant, the acceleration is thus zero.
The equations for the position in each direction correspond to the equation of a straight line in the three dimensions space.
The uniformly accelerated rectilinear motion
Another simple problem is when the acceleration is constant. Similarly to the URM, here we easily find the speed:
And the position: