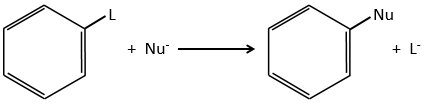
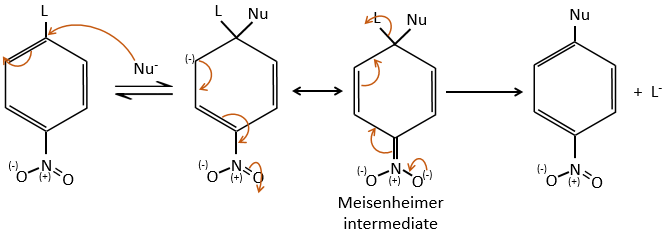
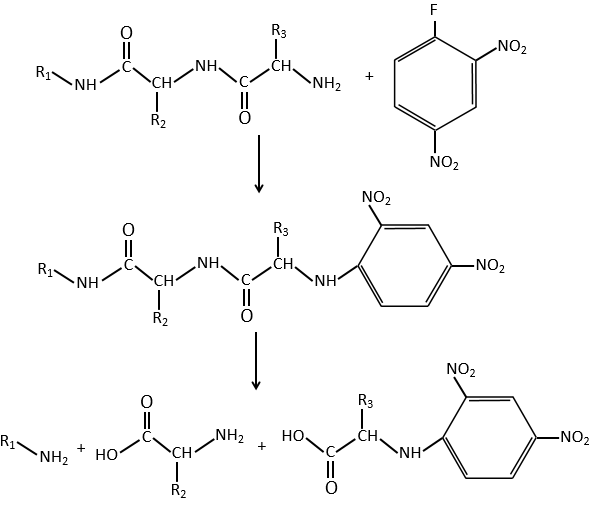
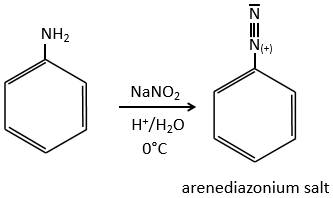
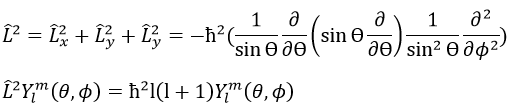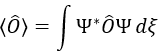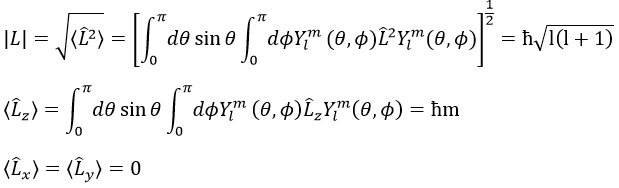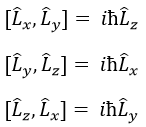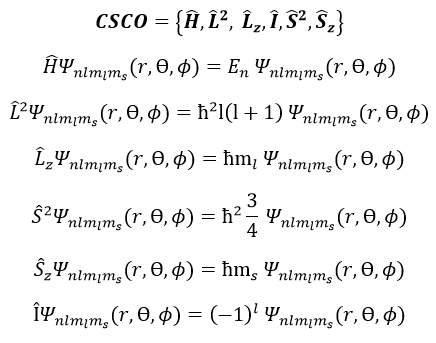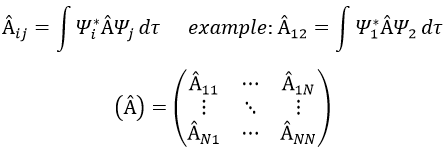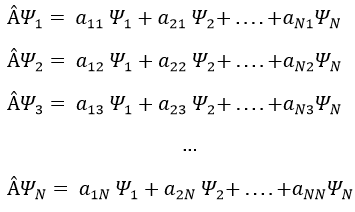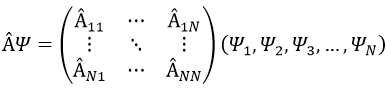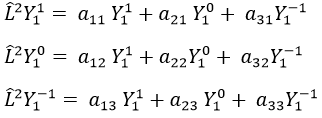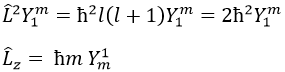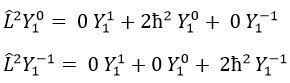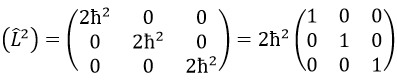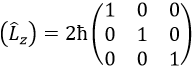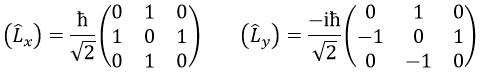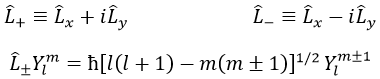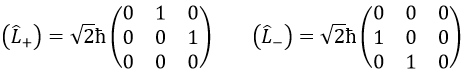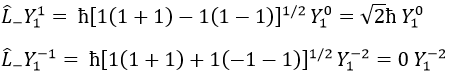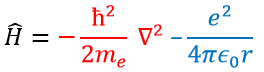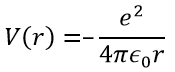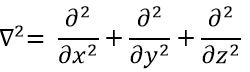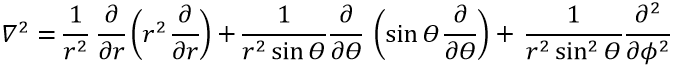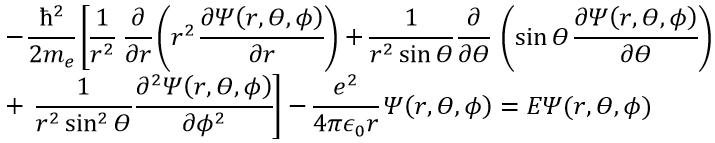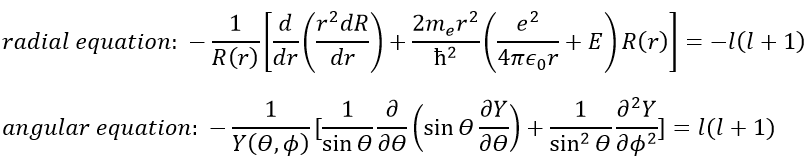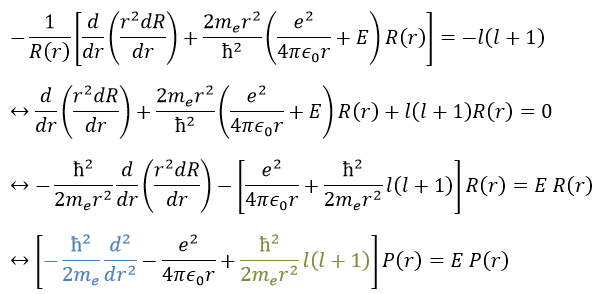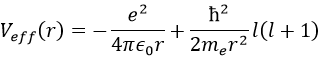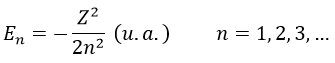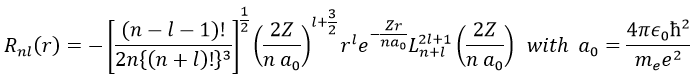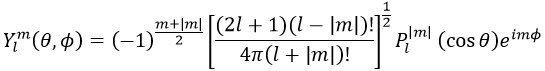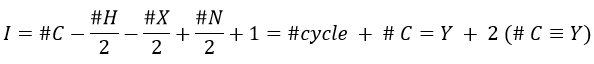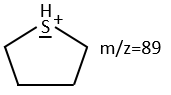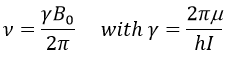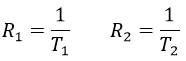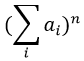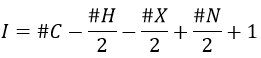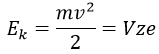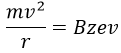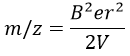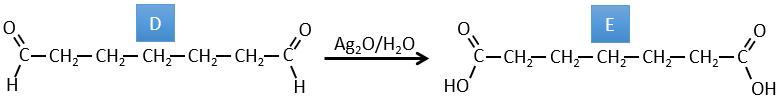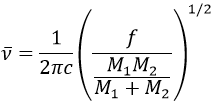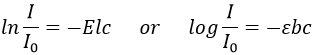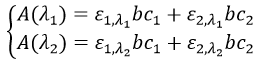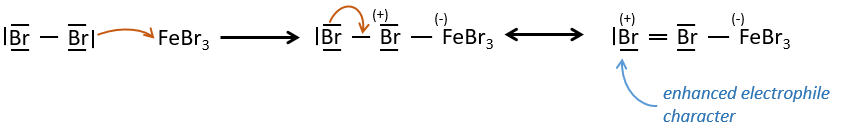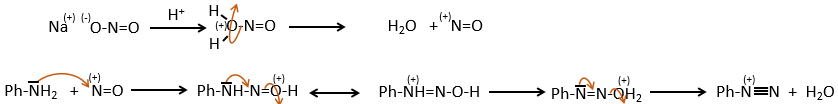Chapter 10 : molecular physical chemistry – operators
Operators can be applied to the wave functions and respect the equation of Schrödinger. The operator inversion Î is an operator such as, if a central symmetry can be found,
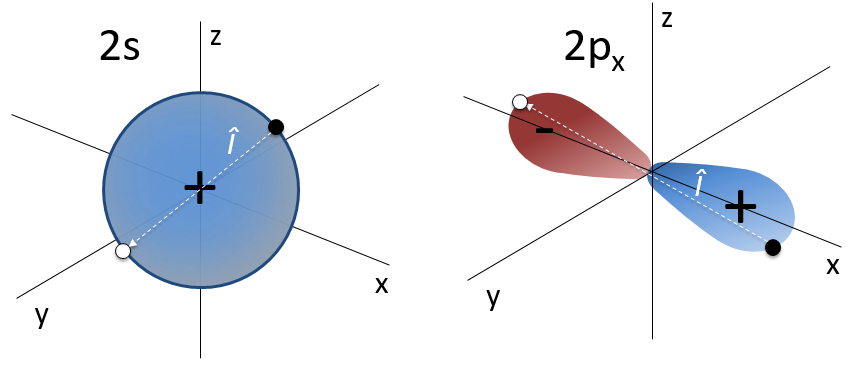
For instance, the orbital s have a centre of symmetry. We say that this state is even. If we apply the inversion operator to this orbital s, the sign of the orbital is still unchanged at the opposite side of the atom (i.e. obtained by central symmetry).
The orbital p is odd because if we look at one point in the positive part of the orbital and apply the symmetry, we are now in the negative lobe of the orbital. The d orbitals are even. If fact, we have
The operator Î can also be applied to electrons to obtain the opposite spin (up à down).
Angular moments
The angular moment L is the cross product of two vectors r and p. The cross product or vector product is a binary operation on two vectors and is denoted by the symbol ×. Given two linearly independent vectors a and b, the cross product, a × b, is a vector c that is perpendicular to both and therefore normal to the plane containing them (two linear vectors always share a plane).
The intensity of the new vector is a × b = ∣a∣∣b∣ sin n (with n the unity vector pointing in the good direction) and the direction of the cross product is given by the rule of the right hand: the index stands points in the direction of the first vector and the middle finger points in the direction of the second vector. If you put your thumb perpendicular to the two other fingers (as to show your approval), it points the direction of the cross product. It can be necessary to rotate your hand strangely to get the good directions, for instance to obtain the b x a product from above.
In quantum mechanics, p is an operator
We have thus
Note that Lz does not depend on and there is thus a symmetry around the z axis for this operator. If we apply the operator Lz on the angular wave function, we obtain the wave function multiplied by ћm:
It means that the angular wave function is a proper function of the operator Lz. It is also the case with the operator L2.
We can thus simultaneously determine the proper values of L2 (=ћ2l(l+1)), characteristic of the angular moment L, and of Lz (=ћm), the projection of L on the z axis, for fixed values of the quantic numbers.
The proper value of an operator is the integral of the wave function multiplied by the operator acting on the wave function:
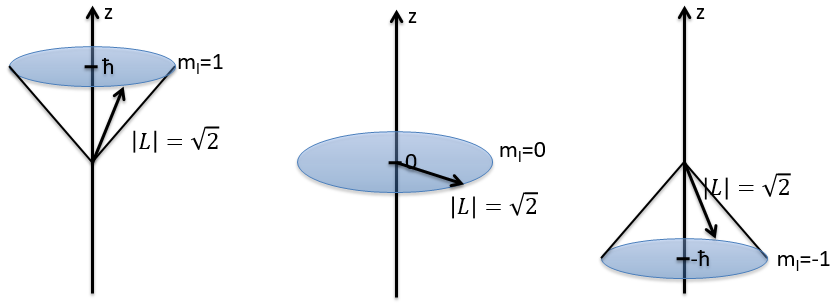
The length of the vector L and of its projections on the axes.
For instance, for l=1, we can draw L and its projection as a function of m. The length of L doesn’t depend on m but the projection on the axis z does.
L2 and Lz commute: two operators that commute have the same wave function. The commutativity means that
It is indeed the case: [L2,Lz]=0 and it is not the case between Lx, Ly and Lz:
Note that Lx and Ly also commute with L2, like Lz does, but their proper values <Lx> and <Ly> equal zero.
The same kind of properties is true for the spin of the electrons with the operators S2 and Sx, Sy, Sz.
To describe the whole system, we have thus a series of equations containing the 5 quantic numbers n, l, ml, s and ms. They form a CSCO (complete set of commuting observables).
Matrix representation
In an orthonormal base of functions {Ψ1, Ψ2,…ΨN}, the operator  has a matrix representation (Â) which is a matrix composed of operators Âij such as
If Ψ1=Ψ2, the result would have been the proper value of Ψ1 if Ψ1 is a proper function of Â. It is usual to use the bra-ket notation of Dirac:
The part before the operator is called the bra and the part after the operator is the ket.
If Ψ1 is not a proper function of  (ÂΨ≠aΨ), then we can find a linear combination (combili) of wave functions such as
or written as matrices
Let’s take an example with the operators Lz and L2 and the angular functions Yml that we used before for l=1. The complete base of functions is Y1m={Y11, Y10, Y1-1}. The equations are
The values of aij can easily be found
The equation for Y11 has no dependence on Y1-1 or Y10. As a result, aij=0 for i≠j and aii=2ћ2.
The same goes for Y01 and Y11
Then we have that the matrix representation (L2) of the operator L2
This matrix is diagonal, i.e. the components of the matrix that are not on the diagonal are all equal to zero. (Lz) is also diagonal
The rule is that if the operators are operators of functions that are proper functions of this operator, then the matrix is diagonal. All the operators of the CSCO have a diagonal matrix representation on the base of their common proper functions. Note that it means that Lx and Ly are not part of the CSCO: they don’t commute with Lz and their matrix representation are
It is a direct consequence of the Heisenberg’s uncertainty principle: we cannot know the exact position and speed of a particle at the same time. As a result, L2 cannot commute with all of the Lx, Ly and Lz.
We can define the operators of climbing L+ and of descent L– from Lx and Ly.
For our example with l=1, they are
Their role is to move from one orbital to another one.
As the last line shows it, it is impossible to move out of the system. There is no Y1-2 orbital.
Chapter 9 : Molecular physical chemistry – the hydrogen
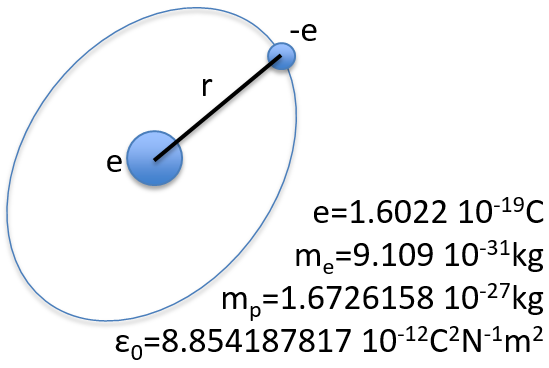
To begin smoothly, we will describe the simplest uncharged molecule: the hydrogen. It is composed of one proton with a positive charge e and one electron of opposite charge –e that revolves around the proton at a distance r.
In quantum mechanics, the system is described by the equation of Schrödinger
Ψ is a wave function and Ĥ is the Hamiltonian, composed of one kinetic term and of one potential term.
The potential term is the potential of attraction between two opposite charges in the void (ϵ0 is the void permittivity).
The kinetic term describes the movement of the electron in orbit around the nucleus, where ћ=h/2π and the gradient ∇ is
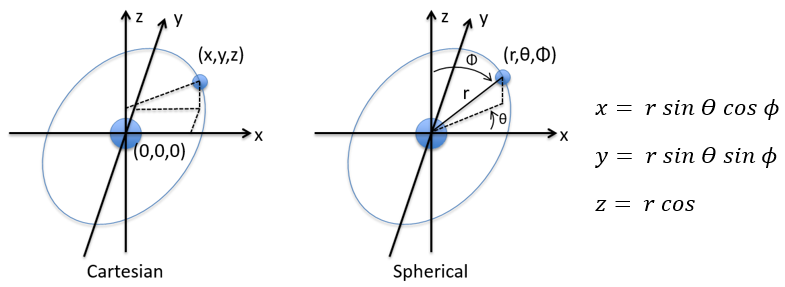
in Cartesian coordinates. It is interesting to change for spherical coordinates. The expression looks more complex but allows to separate some expressions.
Then
This expression seems more complex than the previous one, but there will be one big advantage. The equation of Schrödinger becomes
This equation, developed, gives
As a result, the wave function can now be separated into one radial equation and one angular equation.
The solution of the equations are directly related to the quantic number l. As a reminder, the quantic numbers n, l and m give the electronic configuration of the atoms with l between zero and n (O ≤ l ≤ n) and m between –l and l (–l ≤ m ≤ l). For instance if n=2, l can have a value of 1 or 0, giving 3 possible values for m: -1, 0 (twice), 1. Fermi told us that we may put 2 electrons of opposite spin on each orbital. For the atoms, the orbitals are noted s, p, d, f, g,… for l=0, 1, 2, 3, 4,… preceded by the quantic number n.
We will first try to solve the radial equation. To do that we multiply everything by ћ2/2mer2 and change the variable from R(r) to P(r)=rR(r).
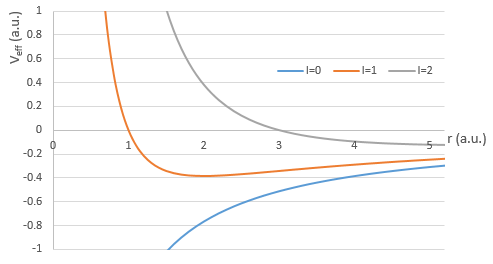
There are three terms in the equation: the radial kinetic energy, the Coulomb potential and the centrifugal term. The equation is similar to the initial Hamiltonian but there is an additional centrifuge term. The potential term is now composed of a Coulomb term (potential of attraction) and of the centrifugal term.
If we consider the effective potential, we see that the centrifuge term repulses the electrons from the nucleus. The s orbitals (l=0) have no centrifugal term and their electrons are thus close to the nucleus. The other orbitals involve a positive centrifugal term moving the electrons away from the nucleus.
The energy En of the orbitals depends on n and not on l or m.
It is proportional to 1/n2. The orbitals are thus closer and closer of each other when n increases. The energy is negative and tends to zero for n→∞, i.e. the ionisation. The energy is also proportional to the square of the atomic number. The energy is thus different for H or He+, or any atom with one single electron despite the similar structure.
The solution for the wave function is
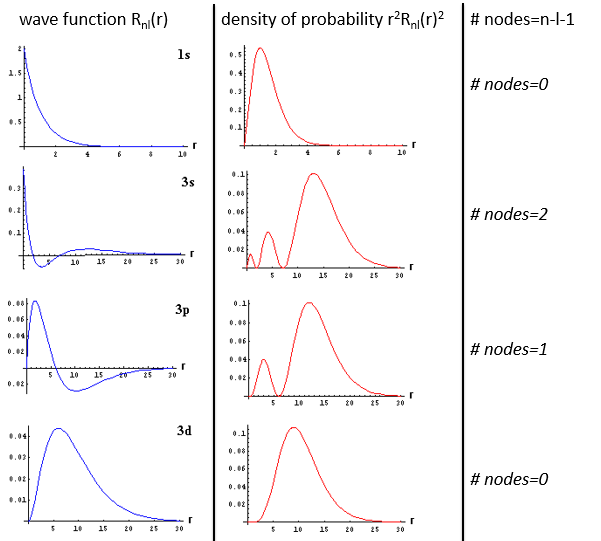
The wave function Rnl(r) will thus depend on the quantic numbers n, l, the atomic number and the radius. In the case of s orbitals, the wave function is not equal to zero at r=0. Yet the density of probability is r2.Rnl(r)2 and there is thus no electron at the nucleus.
As the density of probability is the square of something, the areas with a negative value of Rnl(r) can possess electrons. The points where the density of probability equals zero are called nodes and their number is equal to n-l-1. Note that there is thus no fixed radius for an electron but for its largest probability of presence and that even if the energy of the orbitals are equal, the electrons are not at the same distance from the nucleus. For monoelectronic atoms, the orbitals 3s and 3p are thus at the same energy. They are degenerated. It is the case for all the orbitals with a same value of n.
Now, let’s take a look at the angular wave function Y.
Where Pl∣m∣(cos ) is the associated functions of Legendre. The solution here does not depend on n but on l and m. A few solutions are given below:
The first angular wave function Y00 gives a sphere as it has no dependence on the angles and ϕ. The other functions have different shapes that depends on the angles.
To obtain atomic orbitals we just have to combine the angular and the radial wave functions. The orbitals s are spherical. There are 3 orbitals p because there are 3 possible values for m: -1, 0 or 1. The orbitals are identical but point in different directions. Actually it is a bit more complicated: the angular wave functions for m=-1 and 1 have an imaginary term that we get rid of by a change of coordinates, back to the Cartesian ones. We can do this change with a combination of the orbitals. We can draw the orbitals with the following technique:
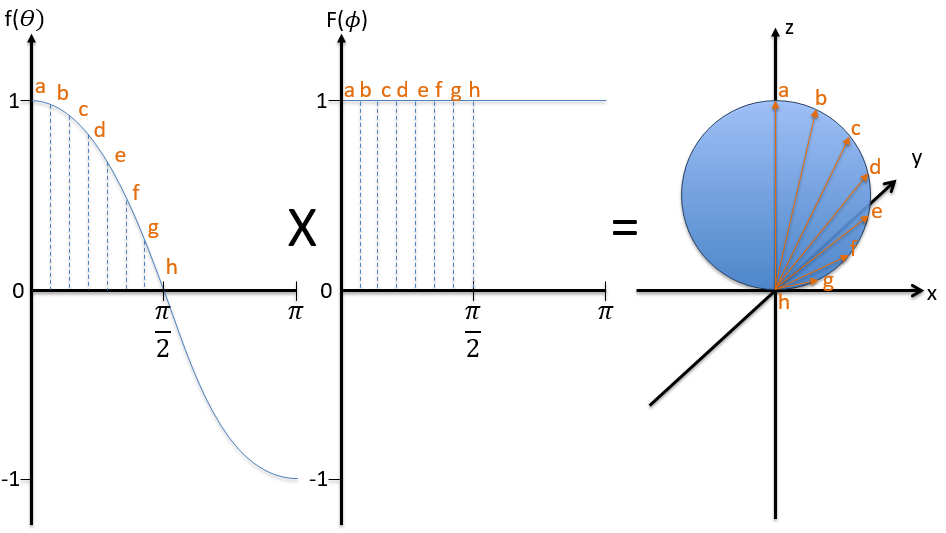
First we take the functions that depend on one angle and draw their value as a function of the angle. For the orbital pz the functions are f()=cos and F(ϕ)=1. While F=1 for any angle, f goes from 1 to -1. The orbital is given by the multiplication of the two functions. F=constant means that the orbital is identical for any value of ϕ. The axis z is thus an axis of symmetry. is the angle in the z direction. When =0 (point a), we are on the axis z and the intensity is 1. When >0, we are not on the axis. The intensity is smaller than one so we draw a point at a smaller distance from the centre than the previous point. The intensity keeps decreasing to reach zero at =π/2 (point g), the intersection with the plane x=0, y=0. In fact, we just drew one sphere above the plane x=0, y=0. The same is done at the other side of the plane (π/2< <π). This part of the orbital has a negative sign because the function is negative (cos <0). We can repeat this method for the other directions.
Chapter 8 : mass spectra – exercises
The solutions immediately follow the problems. You can use this website to find fragments corresponding to a given m/z ratio: MS fragments. The methodology to obtain the answer is given.
Problem 1
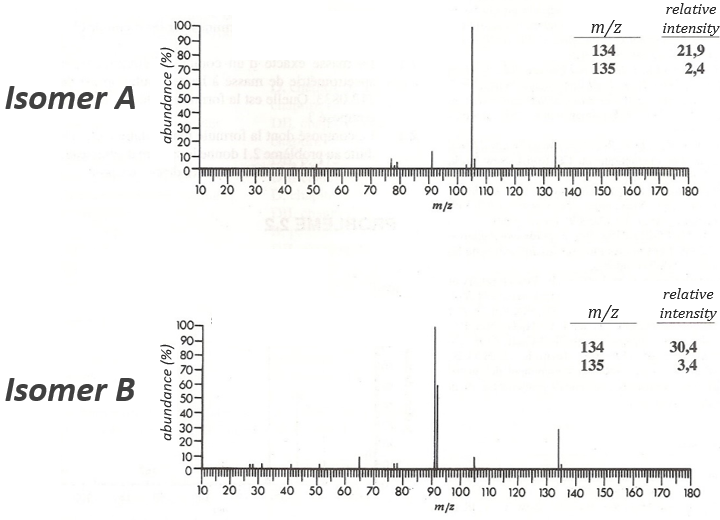
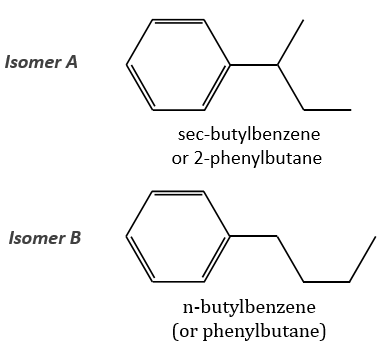
The two following spectra come from two isomers with the formula C10H14. Determine the structure of each of them.
Answer
The isomer A is the sec-butylbenzene (or 2-phenyl-butane) and the isomer B is the n-butylbenzene (or phenylbutane).
Explanation
The composition of our unknown species is given in the wording: C10H14. The first thing to do is thus to determine the degree of unsaturation of the species.
In our case I=4, indicating a phenyl group somewhere in the molecule. It is confirmed by the presence of a peak at m/z=77 (benzene, often with a cluster at 78 and 79) and at 91 (tropylium) on both spectra. The peak of the tropylium at m/z=91 is way more intense for the isomer B than for the isomer A, indicating that the formation of ϕ-CH2+ is somehow less stable in the case of the isomer A. Indeed, the tropylium ion usually shows a very intense peak as we can see on the spectrum of the isomer A.
In our case I=4, indicating a phenyl group somewhere in the molecule. It is confirmed by the presence of a peak at m/z=77 (benzene, often with a cluster at 78 and 79) and at 91 (tropylium) on both spectra. The peak of the tropylium at m/z=91 is way more intense for the isomer B than for the isomer A, indicating that the formation of ϕ-CH2+ is somehow less stable in the case of the isomer A. Indeed, the tropylium ion usually shows a very intense peak as we can see on the spectrum of the isomer A. It is the main difference on which we will base our analysis.
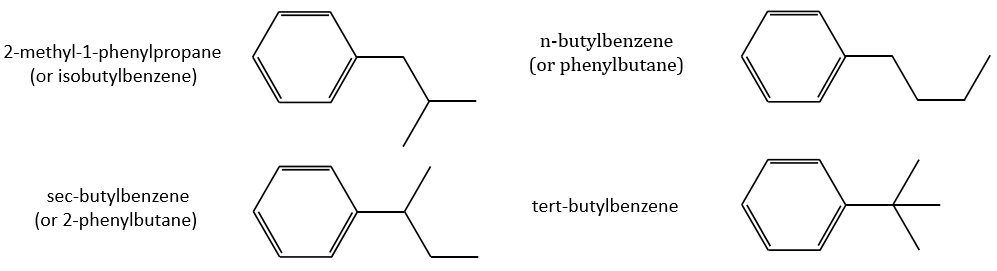
Removing the phenyl from the composition, we find the composition of a butyl group (C4H9). The question is how those 4 carbons are placed around the phenyl but we have already limited by a lot the number of possibilities. We can assume that the 4 carbons make one chain bound to the phenyl and not 2 or more for the isomer B. Let’s focus on this isomer for now. There are 4 possibilities to bind a butane and a phenyl together:
From the intensity of the peak at m/z=91, we can reject the possibilities of the bottom. The two last possibilities, the n- and iso-butyl~ have very similar spectra and both can explain the peak at m/z=92. This peak comes from a rearrangement of Mc Lafferty transferring one proton from the carbon in γ of the phenyl.
We will favour the n-butyl~ because there is a peak of good intensity at m/z=105, i.e. +14 to the tropylium that is hard to explain (and almost inexistent) in the case of the iso-butyl~.
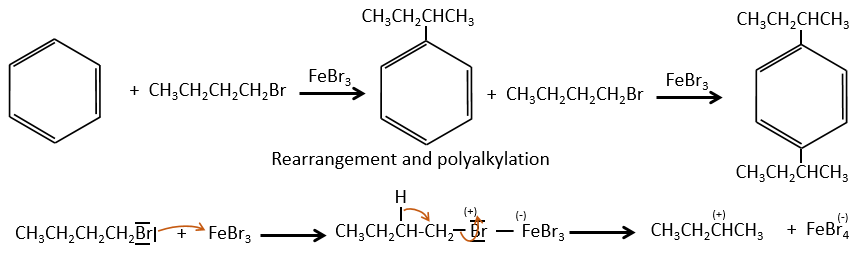
The isomer A can be the sec-butylbenzene that was on our list of 4 structures matching the binding of a butane with a benzene. The obtaining of a tropylium is hard in this case because there are multiple liaisons in α of the phenyl. Moreover, the fragmentation favours the removal of the most substituted fragments from the chain if there are several substituents. The phenyl can be removed (but aromatics are usually not removed from fragments) but also the ethyl chain, what leads to a peak at m/z=105, i.e. the main peak of our isomer A. We can also note the presence of a small (yet existing) peak at M-15. It means that there is a methyl substituent that can be removed. It is less probable than the removal of the ethyl but it can occur. It is thus a good call.
A second possibility is that there are two chains bound to the phenyl, one methyl and one propane. The methyl substituent would the displacement of the tropylium peak by Δm/z=+14 but that’s not how it works. The ion formed would not be as stable as the tropylium and the peak would not be that intense.
The isomers A and B are thus the sec-butylbenzene (or 2-phenylbutane) and the n-butylbenzene (or phenylbutane).
Problem 2
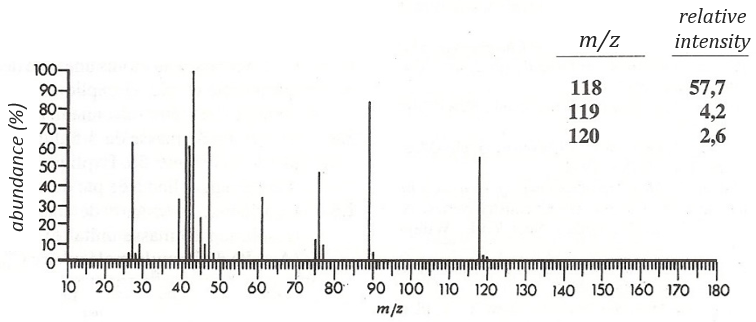
Determine the structure of the compound the spectrum of which is below.
Answer
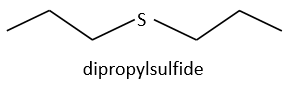
Dipropylsulfide (iupac: 1-(Propylsulfanyl)propane)
Explanation
The first thing we (always) do is to look at the parent peak. The mass (M=118) is even, what means that there is an even number of nitrogen in the molecule. More interesting, there is a peak at M+2. Its intensity is about 4.5%, meaning that there should be a sulphur atom in the molecule. If we remove the mass of an atom of sulphur (M=32) from the mass of the compound, we obtain 74, i.e. the mass of C6H14. The M+1 peak is approximatively 7% of the parent peak, in good agreement with the 6 carbons of our guess (1.1% by carbon à 6.6%). Just from the parent peak and the M+1 and M+2 peaks, we have found the composition of the compound. Now, there are a lot of possibilities to place a sulphur in an alkyl chain. So far we just now that there is no cycle in the molecule (otherwise we would have 2H less).
We will thus analyse the fragmentation peaks. The base peak is at m/z=43 and is surrounded by a cluster of intense peaks. The second most intense peak is at m/z=89, i.e. M-29. It corresponds to the loss of a -C2H5 fragment. The liaison between the sulphur and a carbon is usually not cleaved so we can assume that at one side of the sulphur, there is at least a chain of 3 carbons. This fragment is particularly well stabilised because of the possible cyclisation of the ion.
The presence of this intense peak limits a bit our range of possibilities from some substituted chains. In all honesty, it is difficult to explain the exclusion of all the species and why the dipropylsulfide is the correct answer but we will do our best.
The first compound we want to try out is the primary sulphide.
Several things may let us think it is the correct call:
- the cleavage in αβ gives an intense peak at m/z=47.
- the cleavage in βγ gives a peak at m/z=61 the intensity of which is usually the half of the intensity of the peak at m/z=47.
- the cleavage in γδ gives a small peak at m/z=75.
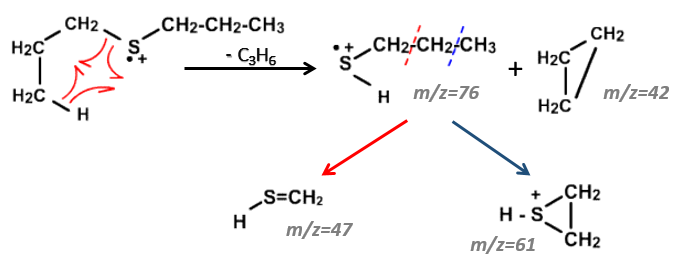
Normally the cleavage in δε gives a peak a bit more intense than at m/z=75 because of the cyclisation of the ion but it is very intense in our spectrum. Moreover, primary sulphide give an intense peak at m/z=34, corresponding to SH2, which is not present at all on the spectrum.
The secondary and tertiary sulphides can be dismissed because of the very strong intensity of the m/z=89 peak. In general, they eliminate the biggest fragment and a very intense peak can thus be observed at M-15, M-29, M-43, etc. Note that we have a very intense peak at M-29. However a peak is usually observed at M-33 (loss of -SH) and there is no trace of it on our spectrum.
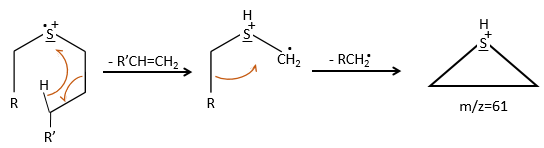
We can thus turn our mind towards the thioalkyls. A cleavage gives the very intense peak at M-29. If we assume that the intensity of the peak is similar than for the primary sulphide, we can guess that the m/z=89 peak corresponds to the cleavage of the αβ liaison. There is thus a side of the sulphur with a length of 3 or more carbons. For those thioalkyls, we find a peak at m/z=61which corresponds to the following fragmentation:
On the spectrum of thioalkyls, we can find peaks corresponding to the cleavage of the liaison S-C, for both the fragment containing the sulphur RS+ but also for the alkyl chain R’+. If the chain is long, the peaks of the alkyl chain can dominate. The base peak of the spectrum is at m/z=43, i.e. C3H7+. This very large intensity can be explained by the fact that the cleavage at both sides of the sulphur in the dipropylsulphide gives this ion. The RS+ peak should be characteristic at m/z=75 but the peak is only of average size. However, there is an important peak at m/z=76. It comes from a particular cleavage leading to the ion RSH+.
Chapter 7 : NMR proton: principles
A full section can be (and will be) dedicated to the detailed setup of the nucleus magnetic resonance (NMR) and to the analyses we can perform with this tool. In this section, we don’t need a lot of explanations on the NMR theory as it is a technique oriented section. We will however give an introduction on the NMR applied to the proton but keep in mind that a lot more can be done.
Principle of the NMR
Similarly to the spectroscopy, when a magnetic field is applied on a sample, some of the electromagnetic radiations can be absorbed, the frequencies of which depend on the properties of the sample. A NMR spectre give peaks of various intensities as a function of the frequency of absorption. Atoms have different reactions resulting from the application of the magnetic field and will absorb in separate regions of frequencies or won’t absorb at all. But more importantly, and that is what interests us in this section, the frequency of absorption of one atom depends on its direct environment. For instance, we can detect the difference of absorption for the hydrogen atoms at the extremity of the chain and in the chain in CH3-CH2-CH3 (δ≈0.91, 1.34, 0.91).
First, let’s come back to the absorption of different atoms. Any nucleus wears an electric charge but in some of them this charge turns in a given direction around the nuclear axis. This movement induces a magnetic dipole than can be described in term of number of nuclear spin I. I can have any positive value starting from 0 and by step of ½, i.e. 0, ½, 1, 3/2, 2, … One isotope has one value of spin that depends on the atomic mass and number of the isotope. We can resume this way:
The number of spin determines the number of orientations that a nucleus can take in a uniform external magnetic field, following the formula n=2I+1. An atom with I=0, such as the carbon 12, can thus only take one orientation and is “inactive” in NMR. Atoms with I≥1 have a non-spherical repartition of the charge described by a quadrupole moment that affects the nearby nuclei.
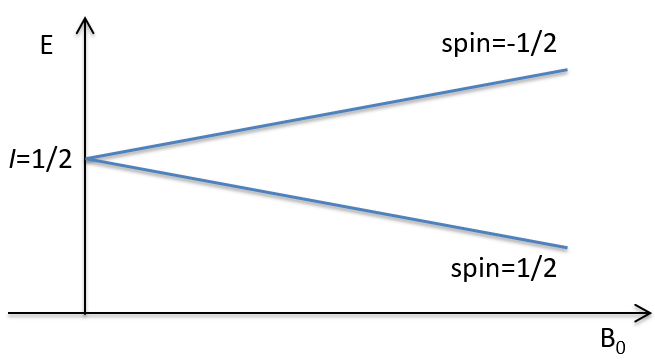
Atoms with I=1/2, such as 1H and 13C can take 2 orientations with different energies corresponding to the spin +1/2 and -1/2. The level of lower energy has a small excess of population that depends on the intensity of the applied magnetic field.
To make the transition between the two levels, quanta’s of energy hν, with ν the frequency of the electromagnetic radiation, are needed in a magnetic field B0. The frequency is related to the magnetic field by the relation
γ is the gyromagnetic constant that depends on the spin I and on the magnetic moment μ. Knowing that, the problem is to find a way to transfer this energy and to measure the absorbed energy.
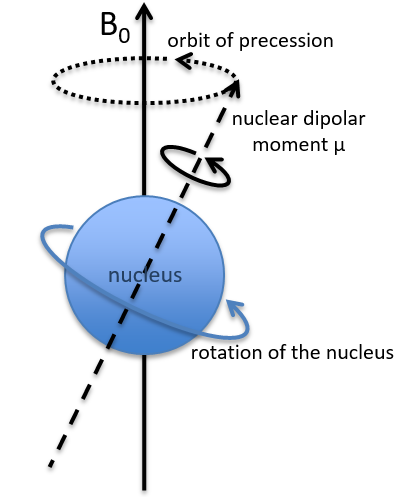
In a magnetic field, a proton turns on itself and around the axis of the magnetic field (see the next figure).
The speed of precession ω0, also called frequency of Larmor is equal to the product of the gyromagnetic constant γ with the intensity of the magnetic field B0.
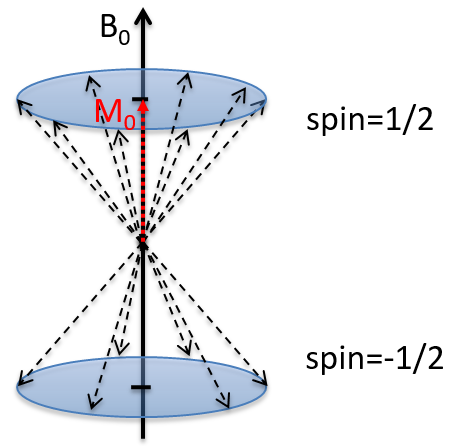
Because of the magnetic field, all the atoms are oriented in the same direction but they are not at the same stage of the precession. Depending on the spin, the orientation in parallel to the field (spin=1/2) or antiparallel (spin=-1/2). As there is a small excess of population for the spin=1/2, a global magnetisation M0 is in the axis of B0 (axis z) but there is no particular magnetisation in the other directions (axes x-y).
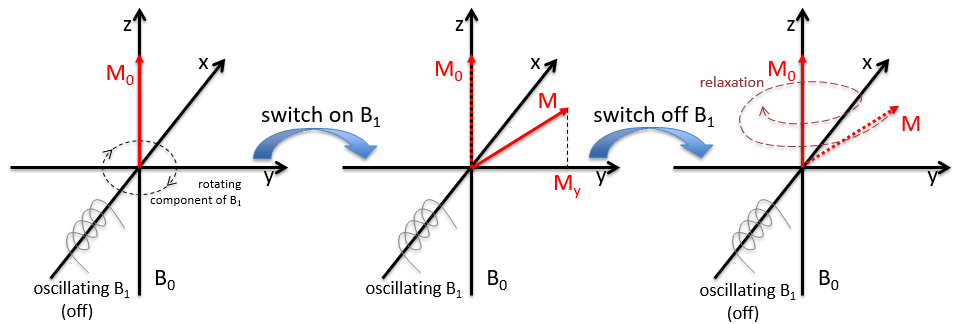
We will tilt the magnetisation towards the horizontal plane using an oscillator that generates a second magnetic field B1 perpendicular to B0. The resulting electromagnetic field rotates at the same speed that the proton. We can detect the generated magnetic component in this plane (My for instance) if desired. Now that the nucleus is excited, we turn the magnetic field B1 off and let the nucleus relax back to its previous magnetisation.
Two methods of relaxation exist. The first is called spin-lattice relaxation or longitudinal relaxation and implies the transfer of the energy of the nuclei to the nearby molecules. This relaxation takes a times T1. The second mechanism of relaxation is the spin-spin relaxation, or transverse relaxation and implies the transfer of energy from one nucleus to a second one. It has a characteristic time T2. We can define R1 and R2 as
To obtain a spectre of NMR, we scan either the frequency of the oscillator B1 or of the magnetic field B0.
Chapter 6 : Mass spectra
The result of the mass spectrometry is given on the form of a histogram giving the abundance of species as a function of their m/z ratio (we write it M as well, as the ions are usually monocharged). It is called a spectrum of mass. The abundance is given in % of the largest peak. No matter how many fragments there are, there will always be a peak with an abundance of 100% and the other peaks have smaller abundances.
Fragments of low m/z are on the left and the parent ion is, eventually, on the right extremity of the spectrum. The parent ion is the molecule that has been ionised but did not generate any fragment. We can refer to its peak as the parent peak or the M peak. Its peak is not always present on the spectrum or it can be small. It is more common to have an intense parent peak in the case of a chemical bombardment for which a peak at M+1 is also intense. Peaks with a larger M than the substrate can eventually exist because of the isotopes.
Rule of the nitrogen
The rule of the nitrogen is a pretty simple rule that tells that if the mass of the parent ion is even, there is an even number of nitrogen in the molecule. If the mass is odd, then the number of nitrogen is odd as well. For instance, there is no nitrogen in C2H6 and the mass is odd: 2×12+6=30. The nitrogen can wear one less hydrogen (NH3) than a carbon (CH4). If we replace one of the carbon by a nitrogen but also has an odd mass, we will have CH3-NH2 with a mass of 12+14+5=31. If we were in presence of NH2-NH2, the mass is odd as there are two nitrogen’s (M=32).
Furthermore, the M peak is usually weak if there is any nitrogen in the molecule.
Isotopic peaks
It is pretty rare when a peak is not directly surrounded by other peaks of lower intensities. Those clusters are due to the presence of isotopes in the fragments. The abundance of 13C is low: 1.1% by carbon in the chain but peaks at M+1 (M being the m/z ratio without isotope) can be observed if the intensity of the main peak is large. It is also possible that two 13C are on the same fragment, leading to a very small peak at M+2. We can estimate the quantity of carbons in the substrate from the intensity of the M+1 and M+2 peaks. The intensity of the M+1 peak is equal to 1.1%n of the intensity of the M peak, with n the quantity of carbon (we also add 0.36% for each atom of nitrogen N in the molecule). Yet, heteroatoms such as O, N and S can also increase the intensity of the M+1 peak. This tip is thus not absolute.
Other atoms can easily be distinguished by the intensity of their isotopic peaks at M+2. Cl and Br have isotopes with high abundances. Fragments possessing one of those atoms can easily be spotted on a mass spectrum. S also shows a peak at M+2 of approximatively 5% of the M peak by atom of S. O shows a very small peak at M+2 (O.2% by atom of oxygen). Finally Si has isotopes giving visible M+1 (5.1%) and M+2 (3.35%) peaks.
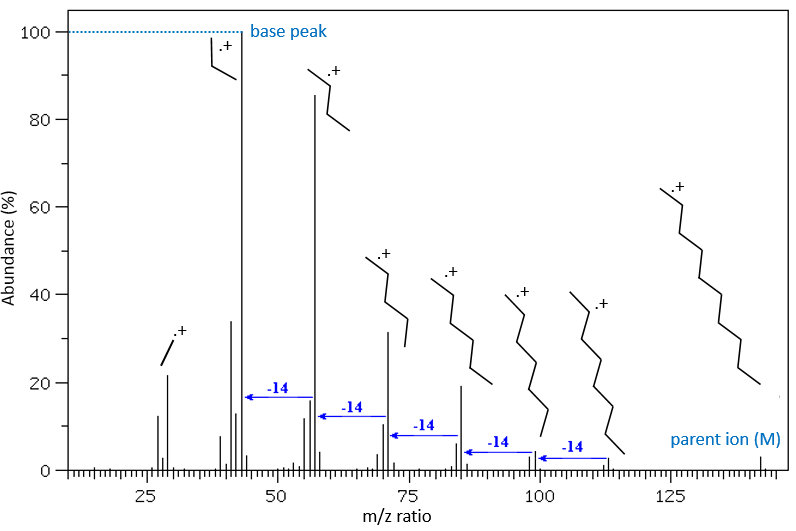
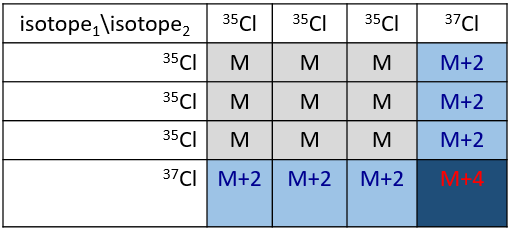
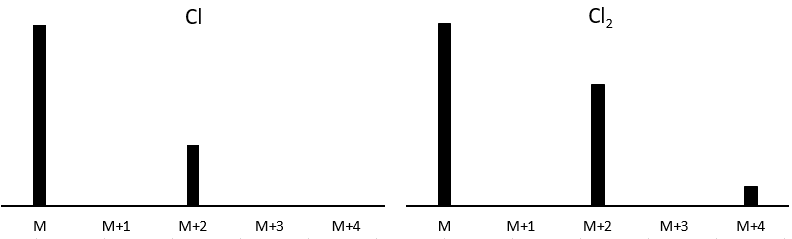
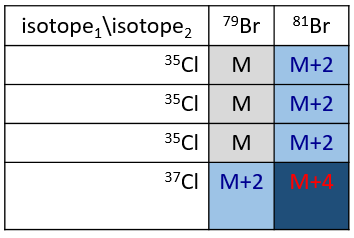
Cl has two stable isotopes: 35Cl and 37Cl. Their abundances are respectively 75% and 25%. On the spectrum, it results in a peak at M+2 with an intensity that is the quarter of the main peak. If there are two Cl on the same fragment, both can be 35Cl or 37Cl or we can have one of each. We will thus have a peak at m/z=M, M+2 and M+4. The intensity of the peaks is still related to the abundance of the isotopes. To make it simple, there are 3 chances on 4 to have a 35Cl and one chance on 4 to have a 37Cl for each of the Cl. We can draw the following table and write the corresponding peak in the cases for the corresponding combination.
There are 9/16 of the fragments that will have the mass M, 6/16 the mass M+2 and 1/16 the mass M+4.The most intense peak is still the peak with two 35Cl. The intensity of the peak with one 35Cl and one 37Cl at M+2 represents 2/3 of the intensity of M and the peak at M+4 with two 37Cl a bit more than 10%.
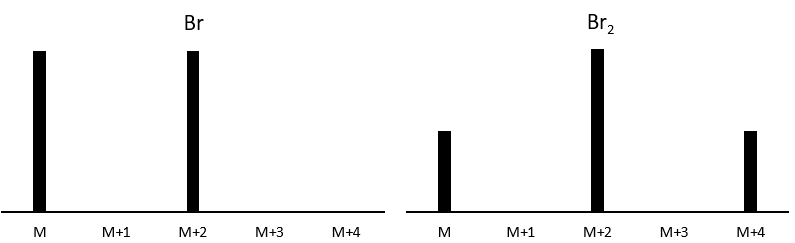
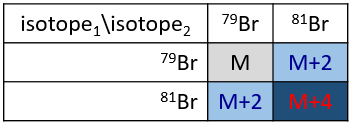
The abundances of the isotopes of Br are approximatively equivalent. If one atom of Br is on the fragment. Two peaks of similar intensities are separated by 2 units of mass. If two Br are on the fragment, the main peak is the one wearing one 79Br and one 81Br (M+2). At M and M+4, the peaks have half of the intensity of M.
If the fragment has 1 Cl and 1 Br, then we have
The relation between the intensities of isotopic peaks (for one type of isotope) is given by the development of the power of a sum
where ai is the abundance of the isotopes i of the atom and n is the number of atoms of the isotope in the fragment. For the example of the bromine, there are two isotopes with equivalent abundances (50%). If there are three atoms of Br in the fragment, we should observe a repartition similar to
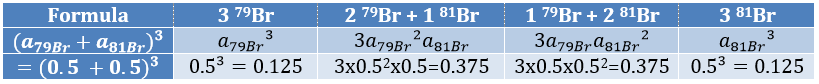
Fragmentation peaks
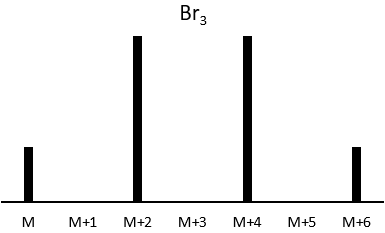
Now that we have analysed the parent peak, we have some advices on the nature on the substrate but we can only guess which molecule it is. A simple example: how would we know if the substrate is the n-octane of the 2-methylheptane?
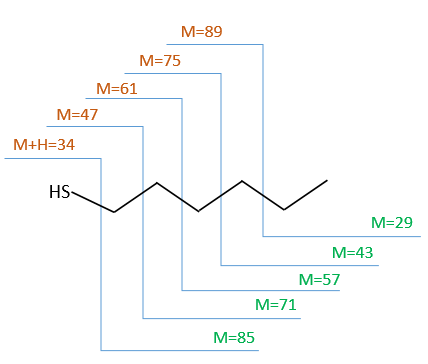
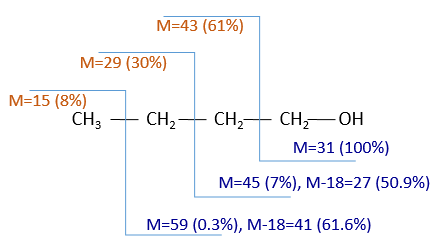
The fragments peaks can help us to find out. To talk about the fragments, we refer to peaks by their m/z ratio. For instance, we can say that the parent ion is at M=m/z=114 and that the base peak is at m/z=43 for both species, and that they have peaks in common (m/z=29, 43, 57, 71 and 114). The intensities of those peaks are not identical and the n-octane shows a peak at m/z=86 and no peak at m/z=99. The fragmentation was thus different because of the structure of the molecule, the composition being identical.
Imagine now that we only knew that the two molecules are alkanes. From the parents ion we can determine that both of them are a form of octane. The interest of the fragmentation peaks will be to give us advices on the structure of the alkanes.
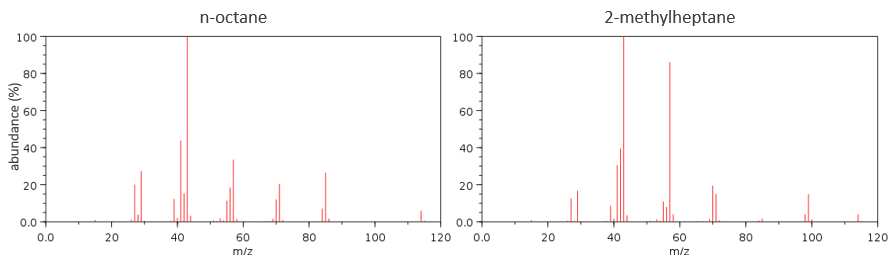
It can be useful to draw the molecules of our guess and cut them into fragments. Virtually, the molecule can break anywhere. A method is to draw the semi-developed representation of the molecule.
To represent the fragmentation at one liaison, we draw a line perpendicular to the liaison and indicate the masses of the fragments at the left and right of the liaison (respectively in orange and green on the figure above). The Z shape drawn on the figure above is more convenient than a simple line in the case of more complex molecules. For instance, if the n-octane is cleaved after CH3-CH2, the fragment of the left has a mass of 29 (units of mass) and the second fragment, i.e. the rest of the molecule, has a mass of 85. These fragments can be found on the spectrum of the n-octane and have approximatively the same abundance. Unfortunately, the abundances of two complementary fragments are not linked. Remember that when we obtain a fragment, only one side of the molecule remains charged and is detected by the MS, the second fragment being neutral and thus not detected.
One can see that the fragmentation at the level of the –CH3 does not appear on the spectrum. It is because the probability of fragmentation for a given liaison is related to the strength of the liaison, to the possibility of a low energy transition and to the stability of the generated fragments. In general, the intensity of the peaks are not identical and it is common to observe one or two very intense peaks amongst the fragmentation peaks. Some general rules may help us to predict the nature of the most intense peaks:
- the intensity of the M peak is the highest for linear chains and decreases with the degree of ramification. One can see it on the previous figure.
- the intensity of the M peak decreases with the mass of the substrate (for similar structures). The fat esters are an exception.
- aromatic compounds usually show intense M peaks. Double liaisons, cycles and aromatic cycles stabilise the molecular ion, leading to an intense M peak.
- the fragmentation is favoured at substituted carbons because it leads to carbocations that are more stable. The series for the stability of carbocations is
The rule is thus similar to the one for the stability of carbocations for SN1. The biggest substituents are usually removed more easily and there is usually no peak at M-15 because CH3+ is not stable. If a peak is present at M-15, it definitively means that there is a ramification in the molecule.
- Double liaisons favour the allylic cleavage to stabilise the carbocation.
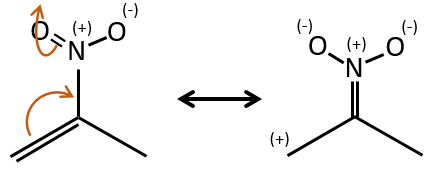
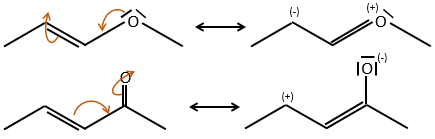
- liaisons nearby heteroatoms are frequently broken because of the possible stabilisation of the charge by resonance.
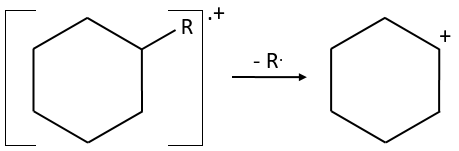
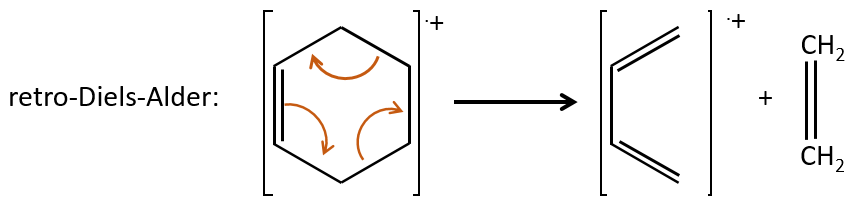
- saturated cycles usually lose alkyl chains and keep the positive charge. Unsaturated cycles are subject to a retro-Diels-Alder reaction.
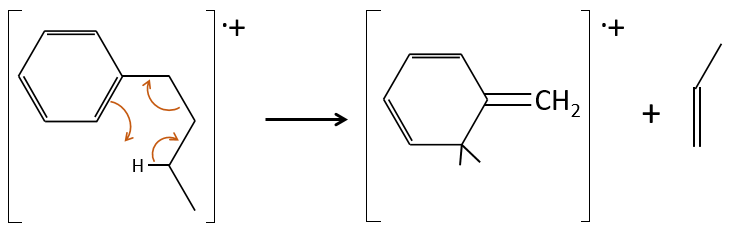
- aromatic cycles usually keep a methyl group and fragment in beta of the cycle to stabilise the positive charge and give the tropylium ion by rearrangement.
- the cleavage is favoured when small neutral molecules can be removed, such as water, H2S, NH3, HCN, CO, etc.
- rearrangement of Mc Lafferty if a hydrogen is in γ of carbonyl. Some fragments cannot be explained be simple cleavages of liaisons from the molecular ion. Such fragments can be the result of an intramolecular rearrangement. The rearrangements often involve the migration of a hydrogen atom on a heteroatom. For instance, a hydrogen in γ of carbonyl can migrate on the O.+. The resulting cleavage is done on the liaison in αβ of carbonyl. It is called a rearrangement of Mc Lafferty.
Typical fragments
There are two ways to look at the fragmentation peaks, and they are used together. The first way is simply to determine what they can be from their m/z, as we have done with the parent peak. There are tables of possible ions corresponding to each m/z ratio.
Here comes a list of some characteristic ionic fragments (that are thus detected on a spectrum):
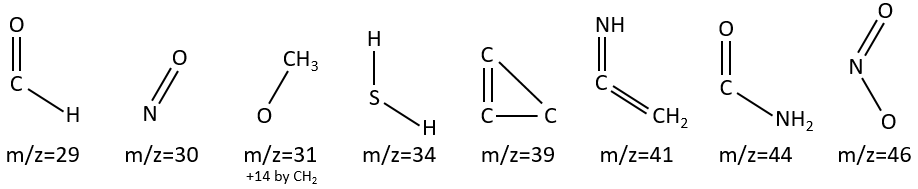
M between 19 and 25: unusual except if there is a O or F.
M=29: presence of an aldehyde.
M=30 (or 46): presence of a nitro.
M=31+n14: presence of an etheric oxygen.
M= 34: presence of a primary -SH.
M=39: presence of a heteroaromatic atom in a cycle of 5 atoms. Several complex cleavages can occur in heteroaromatics, giving respectively the ions C3H3+ (m/z=39), HCY+ or CH2Y+.
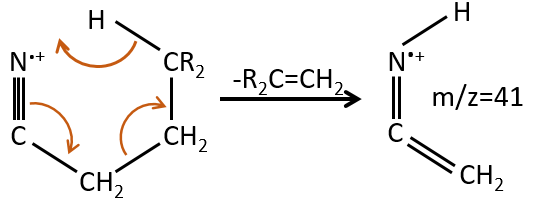
M=41: presence of a nitrile (if Mc Lafferty).
M=44: presence of a primary amide (if Mc Lafferty).
M=46 (or 30): presence of a nitro.
M=47: presence of a sulfur.
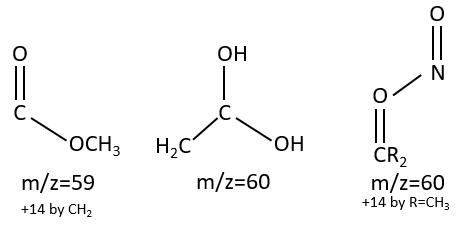
M=59+n14 (clusters): presence of an ester.
M=60: presence of an acid (if Mc Lafferty).
M=60+n14: presence of an aliphatic nitrite.
M=61: primary or secondary -SH.
M=77: this peak is intense and is characteristic of aromatic cycles. It represents the fragment C6H5+. This peak is often in a cluster of peaks (C6H5-6-7) and is accompanied by a peak at M=91 for the toluene/tropylium ion.
M=97: presence of a nitrile (if Mc Lafferty) with a long chain able to form a cycle of 6 carbons.
The other way is to determine which particle has been lost from the parent ion (or from another fragment) to obtain the fragment we are looking at. On the spectrum of the linear alkane that we have seen at the beginning of the section, there is a regular Δm/z=14 between fragments, corresponding each time to the removal of one CH2 fragment of the chain.
It does not mean that the parent ion broke into one fragment by losing one CH2, then that that fragment loses CH2 afterwards, that itself loses CH2 etc., but that the parent ion can break at several places of the chain with a given probability proportional to the intensity of the peak. If the chain is not linear, the distances between the fragments are not so regular. It is why we can say that the spectrum of the left is the one of the n-octane and the second spectrum is the one of the 2-methylheptane.
Here comes a list of some characteristic fragments (neutral or radicals) that can be removed from the molecule:
M-15: -CH3
M-18: -H2O
M-30: -NO
M-31: -OCH3
M-33: -SH
M-45: -COOH
M-46: -NO2
The presence of halogens, spotted by the presence of intense peaks at M+2/M+4 can also be confirmed by the presence of a peak at M-X with X the mass of the halogen.
Confirmation of the composition and structure
Once we determined enough fragments (present on the spectrum and lost), we can try to puzzle them together. At this point, we should have a clear idea of the formula of the molecule. With the formula, we can determine the degree of unsaturation of the molecule. It is given by
For instance, C7H7NO has a degree of unsaturation I=5. The atoms that are bivalent, such as O, are not counted. The atoms with the same valence than C, H, N and O have the same value of unsaturation. S has a value of 0, P has a value of +1/2, etc.
One unit of I represents 1 double liaison or one cycle. Triple liaisons are counted as two double liaisons. A phenyl has thus a value of 4 (3 C=C and 1 cycle).
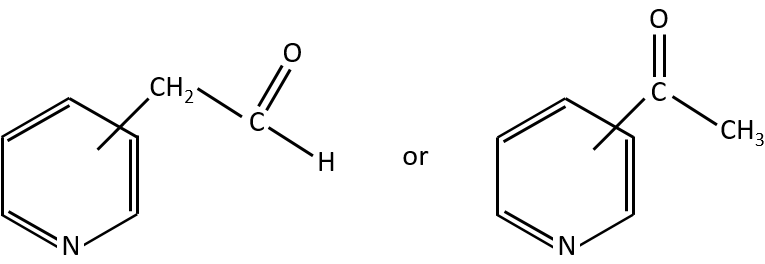
Y can be a carbon but also a heteroatom. The molecule corresponding to the formula C7H7NO can thus be
In combination with the mass spectrum, we should be able to determine which molecule it is.
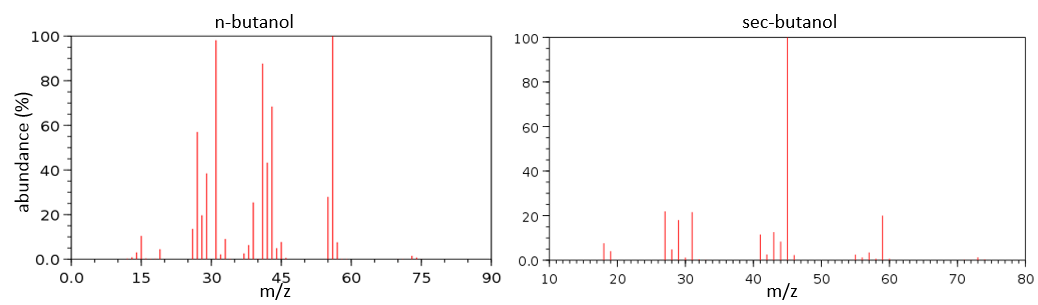
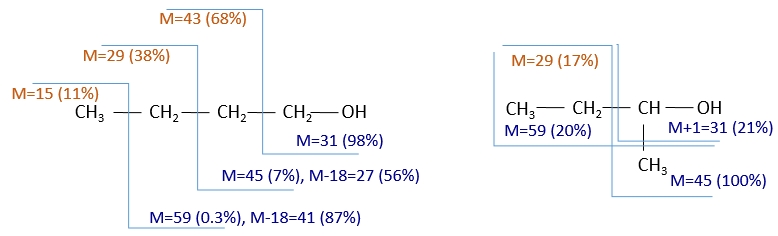
To check our guess, it can be useful to draw the molecule and cut it into its fragments. For instance, the n-butanol and the sec-butanol have two very different mass spectra. Some peaks are on the same location but their intensities are different, referring to the probability of cleavage at a given liaison. It is not necessary to explain all the peaks.
We gave here a strong resume of the mass spectrometry technique and of the analysis of a spectrum. The manual analysis of a spectrum is something that you learn by doing it again and again and that may require some guessing (sometimes some small peaks are important to determine the structure of the molecule and some intense peaks are clueless, like the peak at 56 of the n-butanol). Each group (alcohol, ether, ester, etc) have particular fragments or rearrangements and it is not the point of this section to describe all of them. It will eventually be the subject of a further section (it represents more than 20 pages in my book of reference (Spectrometric identification of organic compounds, Silverstein, Basler, Morill) and the tables for the fragments are 50 pages long, ≈150 fragments per page.
Despite its huge power, there are often several structures than can correspond to one mass spectrum. Usually, the mass spectrometry is used in combination with IR/UV spectrometry and/or NMR. Combined together, we can determine not only the structure of the molecule, but also the exact conformation. We will discuss those techniques in the following sections.
Chapter 5 : Mass spectrometry
Mass spectrometry is one of the most used technique in laboratories because it allows to determine the structure of one molecule. For this technique, the sample should be a pure solution, containing only one molecule that will be analysed within a very short time period. It is why mass spectrometers are often queuing a chromatographic column (HPLC or GC). The solution leaving the column is separated in small samples that are directly analysed in the mass spectrometer.
The principle is quite simple: we destroy the molecule with a bombardment of electrons or cations and we detect its bits, gaseous ions.
The cleavages of the molecules are not totally random and obey a few rules. As a result there are some characteristic ions the nature of which can directly be determined. The detection of the ions is done as a function of their ratio mass/charge m/z (and thus their mass). The mass of the ions is the addition of the mass of the atoms that composes them. Note that the mass written on the Mendeleev table (the chemical mass) is not the mass of an atom but the pondered addition of the masses of its isotopes. The use of the chemical masses is relevant in the case of macroscopic solutions but in the case of the mass spectrometry, we are detecting each single ion so the atomic masses have to be used. The fact that different isotopes of a single atom are in the sample can even give us advices on the nature of the ionic species. To find out which molecule was in the sample, we puzzle the fragments together. There are some programs that can do the puzzling by itself.
The spectrometer of mass
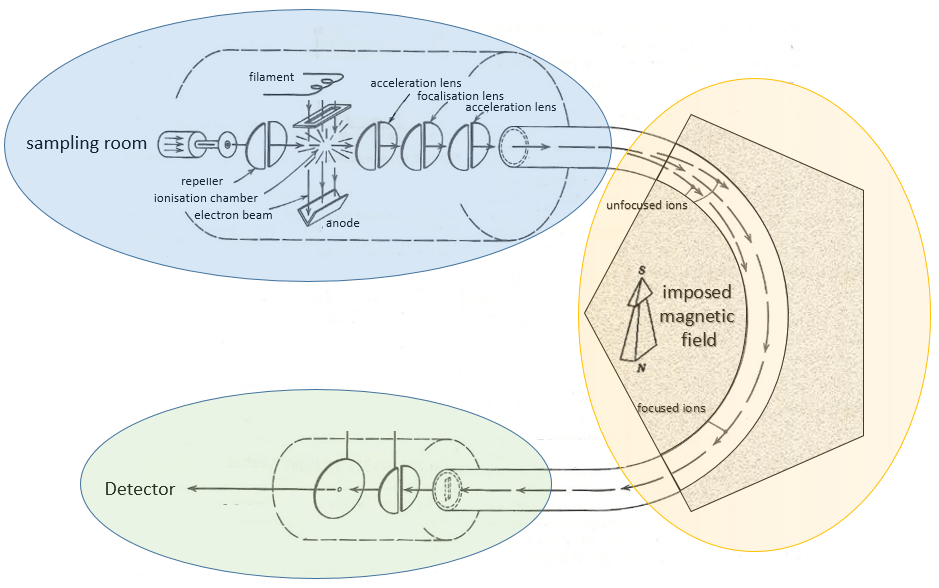
The principle of a spectrometer of mass is to deflect or accelerate ions from or towards a detector in function of their masses. Several models of MS exist and it is not the point of the course to describe all of them but it is still important to understand how the MS works. A spectrometer is always composed of a few characteristic compartments:
- an ionisation chamber
- a separator/analyser
- a detector
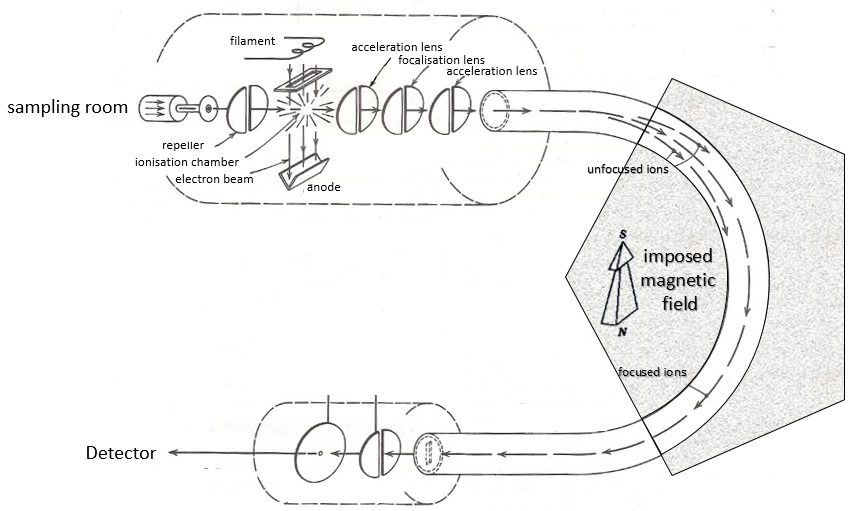
Here is a diagram of one mass spectrometer with magnetic deflection.
We will describe briefly each part.
Sampling
The first step of the analysis is to ionise the sample. It is done in an ionisation chamber. There are three ways to introduce a sample in this chamber:
- direct introduction system: the sample is placed in a capillary that is set in the ionisation chamber. In this chamber, the pressure is extremely low (≈10-5 torr): the void is expected to avoid any recombination between the ions. The difference of pressure will transport the sample to where it will be ionised. This method is used for samples that are not volatile.
- reservoir system: the sample is injected in a reservoir oven heated at a given temperature. The samples that are volatile become gaseous and are transported towards the ionisation chamber by a difference of pressure. The pressure in the reservoir is set to 10-2 torr versus 10-5 torr in the chamber.
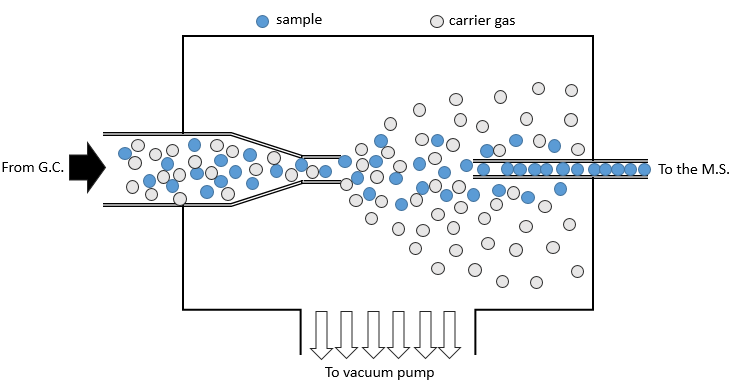
- from chromatography: a gaseous sample comes directly from a GC (gaseous chromatography). Before the introduction in the ionisation chamber, we separate the substrate from the carrier gas . The mass of carrier gas is in general way smaller than the mass of the substrate. We can use this difference to separate them: a thin tube is in front of the exit of the GC. A pump is placed perpendicularly to pump out the gas. As the carrier gas is lighter than the substrate, it is more deviated and does not reach the exit tube. The sample is thus purified.
Ionisation
The goal of the ionisation is to form positively charged ions from the substrate. To do so, the sample is bombarded (by electrons or by cations) to expulse more electrons from the molecules.
The typical range of energy that is required for the ionisation is 8 to 15 eV. As we want to be sure that the substrate is ionised, we inject more energy than required (50-70eV). It is possible to get a double ionisation. The excess of energy can break the ion into smaller ions.
This process can be repeated several times and from one substrate we can have dozens of fragments.
There are two methods of ionisation:
- electronic bombardment
A beam of electrons comes from a heated metal such as a tungsten filament. The electrons collide perpendicularly with the substrate to produce the ionised species that are directed towards the detector by a repeller. The neutral molecules (not ionised or resulting from subsequent cleavages) are removed through a pump
- chemical bombardment
This method is sweeter than the electronic bombardment. It leads to less fragmentation. The energy of ionisation is given by the collision with cations that eventually give a proton to the substrate, increasing its mass by one unit (it is important for later).
Analyser
The difference between different models of mass spectrometers essentially lies in the separation method they are equipped with.
The ionised species are not directly sent to the detector. Before that they have to pass through an analyser. Its role is whether to block some of the species before the detector or to separate them on their way.
Flying time
As simple as it sounds: the ionised molecules are accelerated straight towards the detector without any deflection. The time between the ionisation and the detection is measured. This time is characteristic of the mass of the molecule (t∼√M): small molecules make the distance in a shorter time than large molecules.
Magnetic deflection
On the way to the detector, an electromagnetic magnet is put on the way to the detector, deviating the molecules by a certain angle in function of the mass of the molecule.
The kinetic energy Ek of the ions is given by the repulsion of the repeller and the speed v of the ions depends thus on their mass m and their charge z.
V is the difference of potential between the acceleration lenses. To reach the detector, ions pass through the magnet and are deflected by its magnetic field B. Only one trajectory leads to the detector, when the centrifugal force equals the magnetic centripetal force, i.e. when
We can thus determine the ratio m/z of the ions that reach the detector as a function of the applied magnetic field B:
The same process can be repeated with a second magnets, in the case of double focalisation spectrometers.
Quadrupole
On their way to the detector, the ionised molecules are surrounded by four long parallel electromagnets.
Parallel magnets are set to one given frequency. It allows to control the trajectory of the molecules with one specific mass/charge ratio. Only those species will have a stable path that is parallel to the magnets and reach the detector. The other species are deflected and will eventually collide with one of the magnet where they lose their charge. A range of frequencies is scanned to allow all of the ionised molecules to reach the detector separately.
Ion trap
The principle is similar to the one of the quadrupole except that the ions are maintained in a room between electrodes. They are not moving towards the detector. The ions which are in resonance with the electric field remain trapped. If we increase the tension, the ions of larger mass are stabilised while the trajectory of the lighter ions becomes instable and they hit the electrodes.
Detector
As we detect single ions, the signal has to be magnified several times. It is done by a series of dynodes that increase the signal first obtained on a cathode. The final signal reaches an anode and has been multiplied by 106-7 on its way.
The accuracy of the setup has not to be extremely high and it would actually change almost nothing. The important is that a difference of 1 unit of atomic mass can be detected.
Chapter 4 : Organic chemistry – Exercises
This section is a full part of the course and contains some reactions that were not addressed in the main course. It is challenging to understand by yourselves some mechanisms with the hints that are in the exercises. If you don’t succeed, don’t worry. The solutions and the description of the reactions are directly following each exercise. However, the parts that have been seen in the course are considered as known and may not be explained in details.
The principle of the following exercises is pretty simple (but the exercises are not): We give you a series of reactions that are following each other but we will only give you some of the reactants and/or of the products. From them you have to reconstruct the whole process and find out which molecule and which structure hide behind which letter.
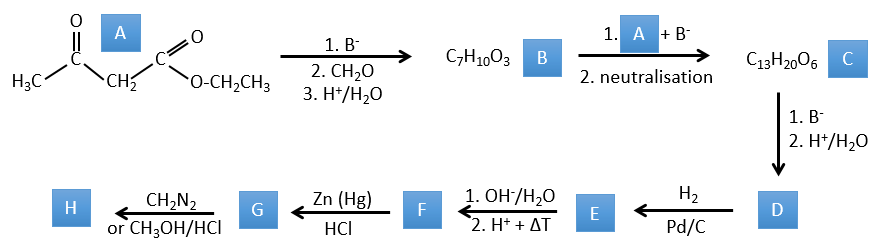
1. In this first exercise you have the structure of the initial reactant (A) and the composition of the first product B. You have to determine the structure of B, the product obtained by the first reaction. Then from B you have to determine the structure of C, then the compound D and its structure, etc.
Correction
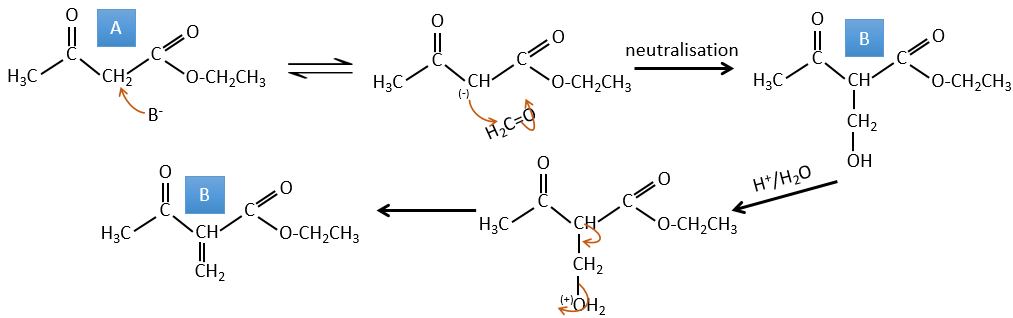
A→B: Two sets of protons are more acid than the others: the protons in α of carbonyl. The protons from CH3 are less acid than the CH2 because CH2 is between two carbonyls. It is thus there that the base attacks. The negative carbon attacks next the formaldehyde. A rearrangement occurs after the neutralisation to obtain B and H2O.
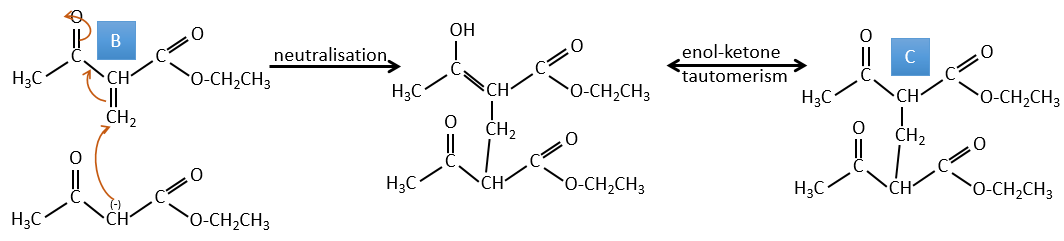
B→C: The first step is identical than for the previous reaction and the two molecules merge together. The attack is done on the sp2 carbon and we obtain a structure that is stabilised by a H bond forming a cycle between the OH and the C=O.
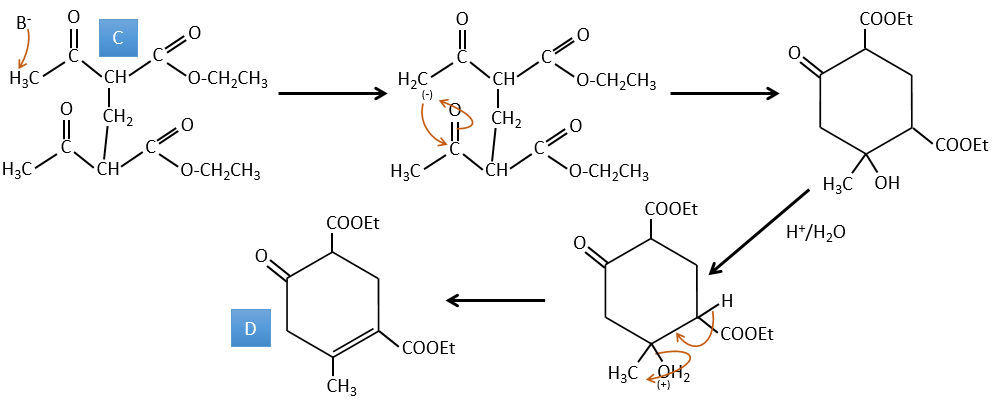
C→D: This time the proton (denoted *) is not attacked by the base because removal of one methylic proton allow the formation of a cycle of 6 carbons. In the second step, the acid catalyses the loss of a water molecule to obtain a double liaison conjugated with the carbonyl.
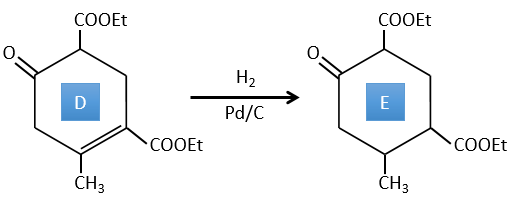
D→E: The double liaison is reduced to obtain a cyclohexane.
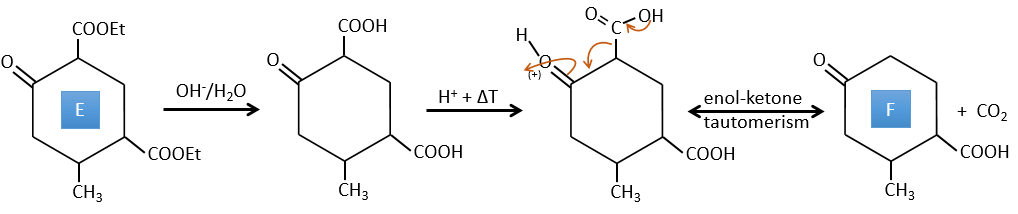
E→F: The esters are turned into carboxylic acids with a basic catalysis. CO2 is lost if we increase the temperature.
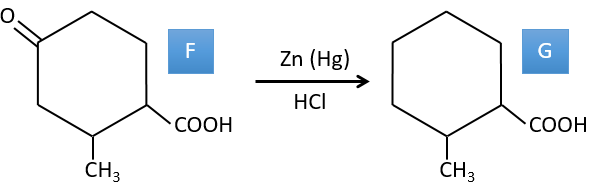
F→G: Zn reduces selectively a ketone into an alkyl chain.
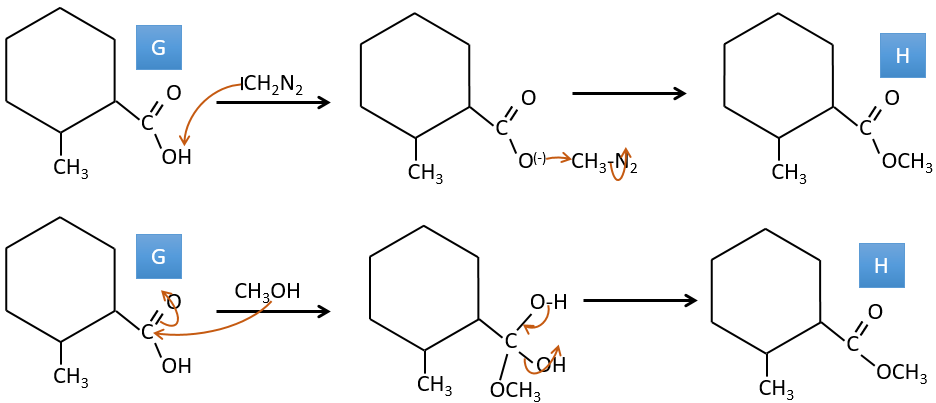
G→H: The diazonium carbene (check nom) is able to take the proton from the acid. The carboxylate attacks next the carbene to form a methyl ester and to free N2. CH3OH leads to the same result but the process is different: There is a nucleophilic substitution on the carbonyl to replace -OH by -OCH3.
2. This exercise focuses on reactions on aromatics and on carboxylic acids and their derivatives.
Correction
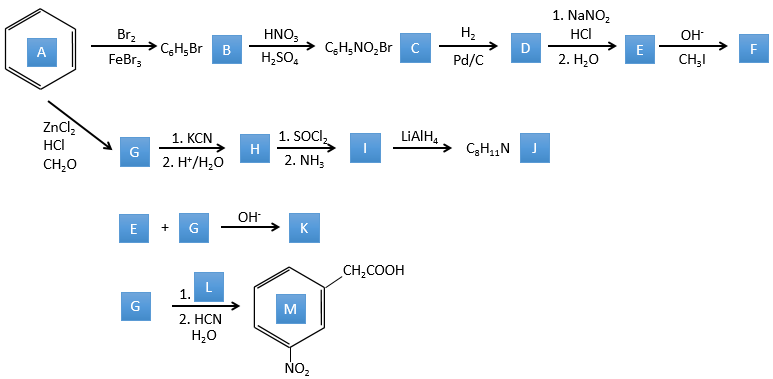
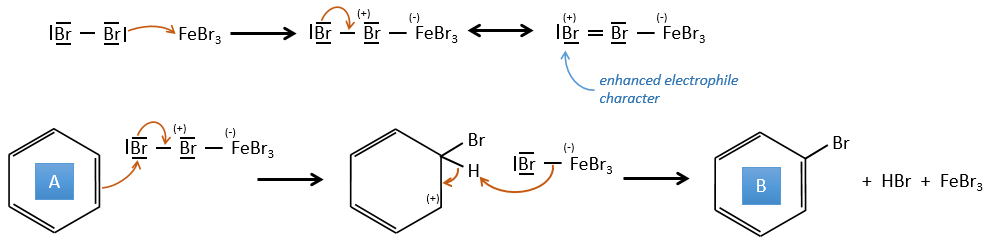
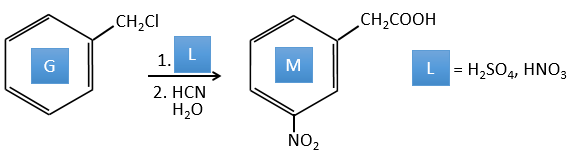
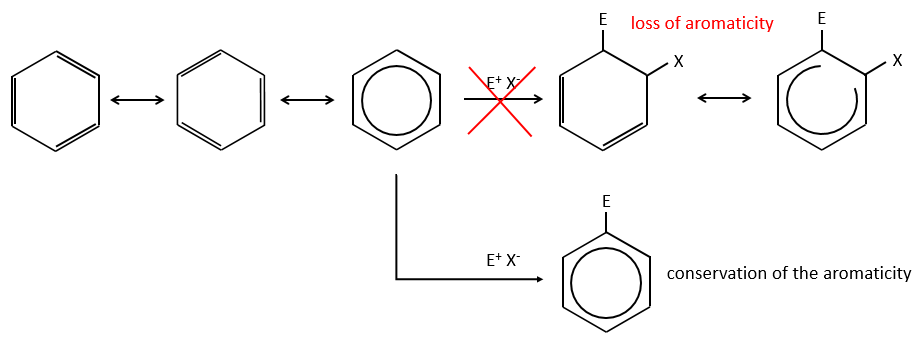
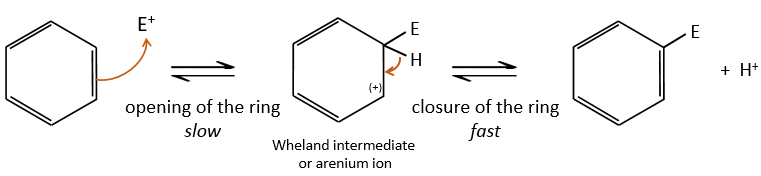
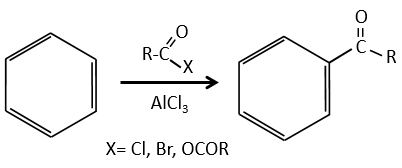
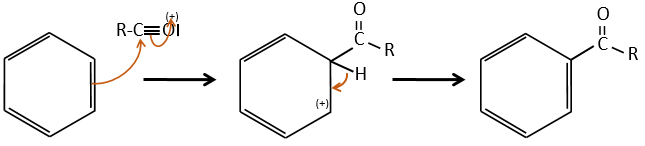
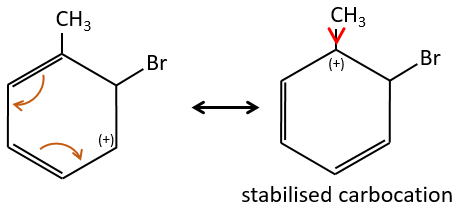
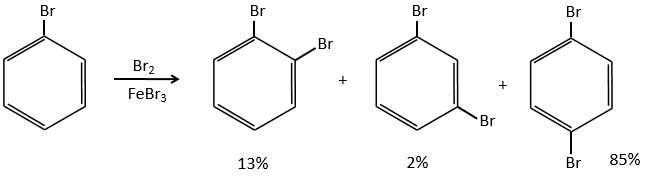
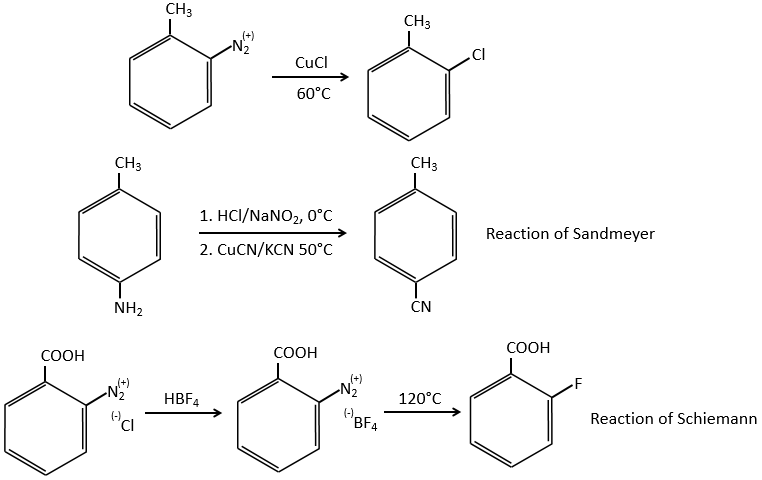
A→B: The electrophile character of Br has to be enhanced by an acid of Lewis to do the reaction.
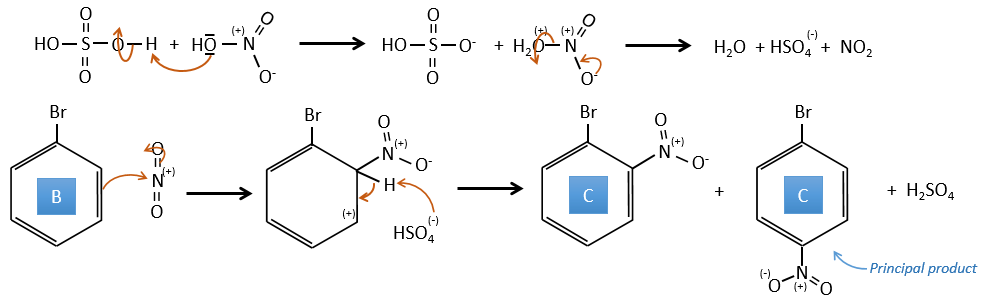
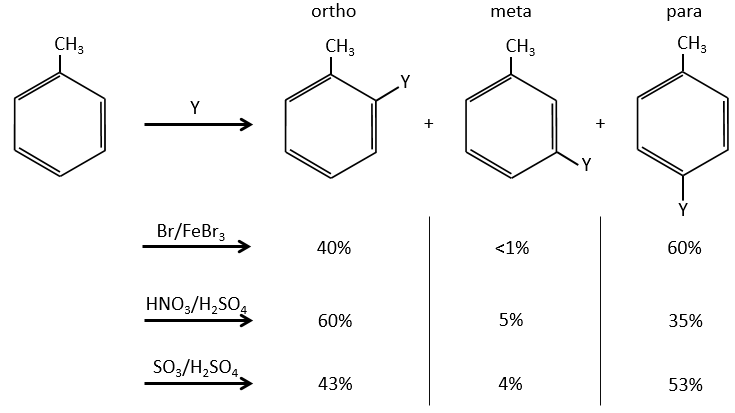
B→C: A nitro group is added to the cycle. There is already one substituent on the cycle so we have to determine if the nitro group is added in ortho, meta or para. A halogen orientates the reaction on the ortho/para positions. The para position should be favoured because of the steric hindrance on the ortho position.
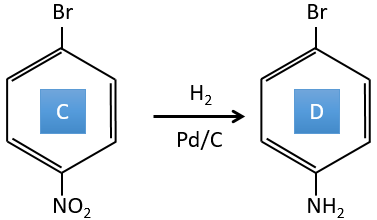
C→D: the reduction is limited to the nitro group that turns into an amine. To reduce completely the aromatic ring we have to heat up the solution to 300°C.
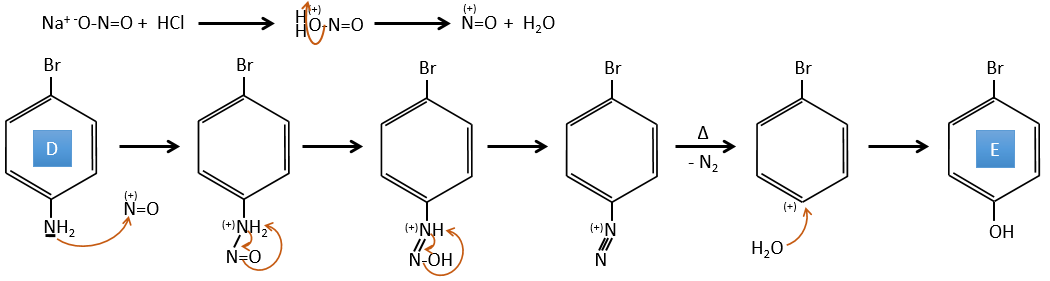
D→E: NaNO2 does not add a nitro group on the ring. It leads to the removal of the amine and the formation of an arenium. This very reactive species reacts with water to replace the amine by a hydroxyl group –OH.
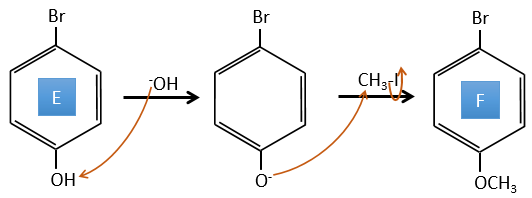
E→F: The base takes the proton of the p-bromophenol. There is then a nucleophile attack by the anion on CH3I to obtain the p-bromometoxybenzene.
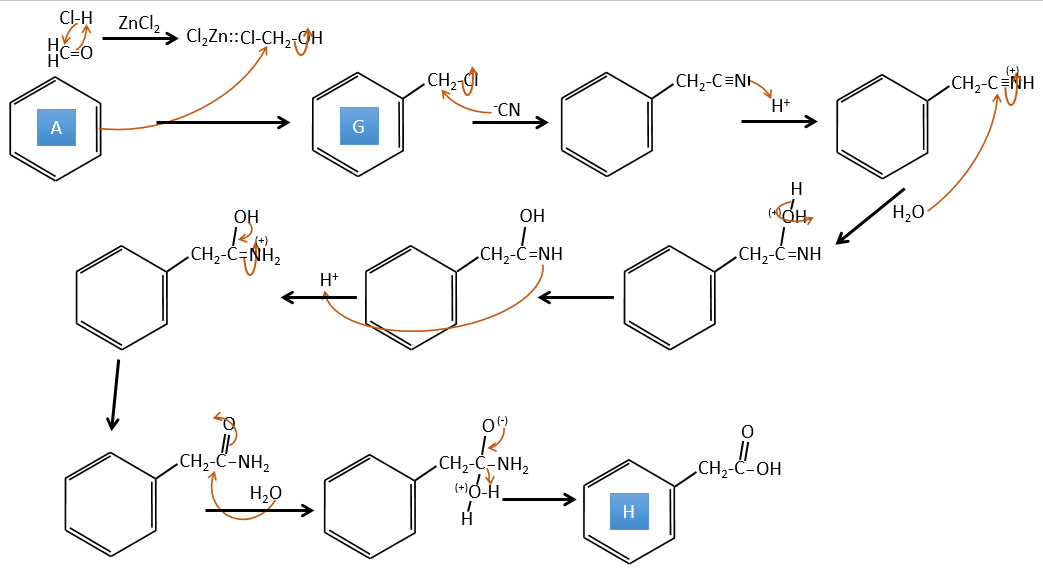
A→G: It is the chloromethylation reaction. During this reaction, the formaldehyde and the chlorydric acid form a chloromethanol stabilised by ZnCl2. The acid protonates the alcohol and the ring can attack it to reject water and bind CH2Cl.
G→H: A simple SN2 by CN– followed by its transformation into a carboxylic acid. This transformation is done by successive attacks of water molecules on the carbon bond to the nitrogen.
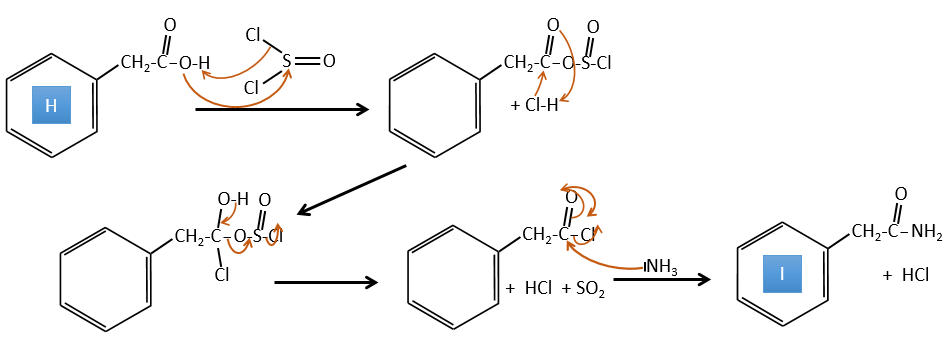
H→I: SOCl2 is a molecule that allows us to obtain an acyl chloride from an acid. It cannot be done with HCl or Cl2 because Cl– is a better leaving group than OH–. The reaction is followed by the formation of a primary amide.
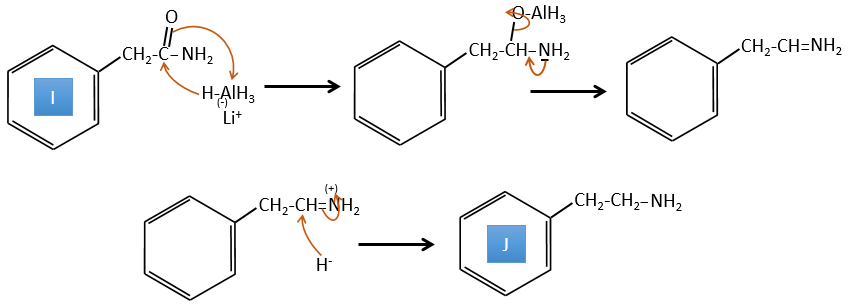
I→J: The amide is reduce into an amine by LiAlH4. LiAlH4 can generates H– that attacks the carbonyl.
E+G→K: A base takes the proton from the bromophenol to obtain a stronger nucleophile. A SN2 takes place between the two species to merge them into one molecule.
G→M: The second step of the reaction leads to the formation of the carboxylic acid as it was the case in the reaction G->H. The missing element on M is the nitro group in meta. This position is favoured because of the mesomeric captor effect of the COOH through the CH2. The effect is however smaller than for a mesomeric captor directly in contact with the aromatic ring.
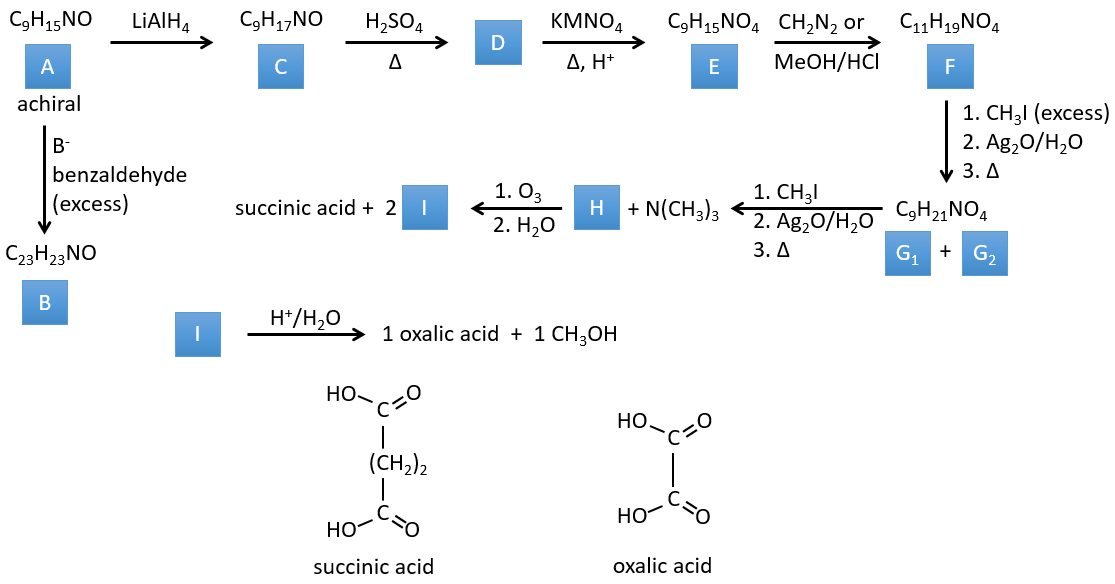
3. In this exercise the last product of a long series of reaction is given. It is the direct product of a reaction of ozonolysis. You have thus to go backwards in the reactions, starting from the end to find the reactants of each reaction. The formulas of most of the molecules are given. G1 and G2 are isomers.
Correction
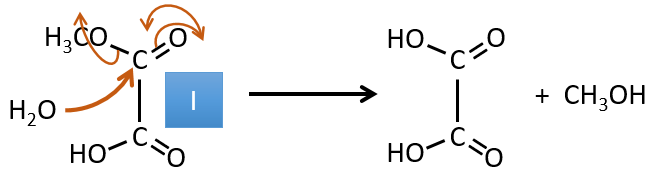
I→…: One of the products, the oxalic acid, is a carboxylic acid and one reactant is the water. We can thus guess that the reaction is a reaction of substitution on a derivative of carboxylic acid. The other product of the reaction is one methanol molecule. One carboxylic acid was thus an ester before the reaction. Only one methanol is generated by the reaction so only one of the two acids of the oxalic acid was an ester.
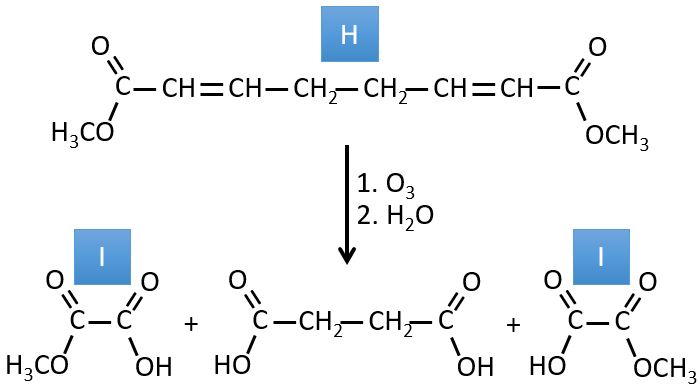
H→I: The ozonolysis cuts a molecule at double liaisons and leads to the formation of carboxylic acids in presence of an oxidant. There are 4 acid groups in the products of this reaction and 2 esters. The 4 acid groups indicate that a bigger molecule was cut down at two places. The double liaisons were thus conjugated with the esters. It is thus an example of reaction that involves a part of the conjugated system and not all of it. We don’t know if the double liaisons are cis or trans.
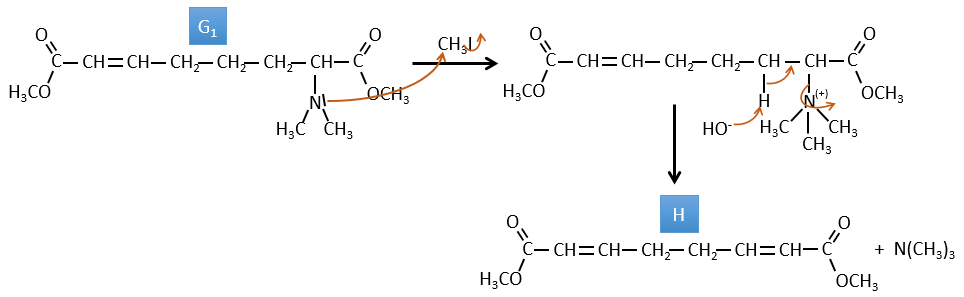
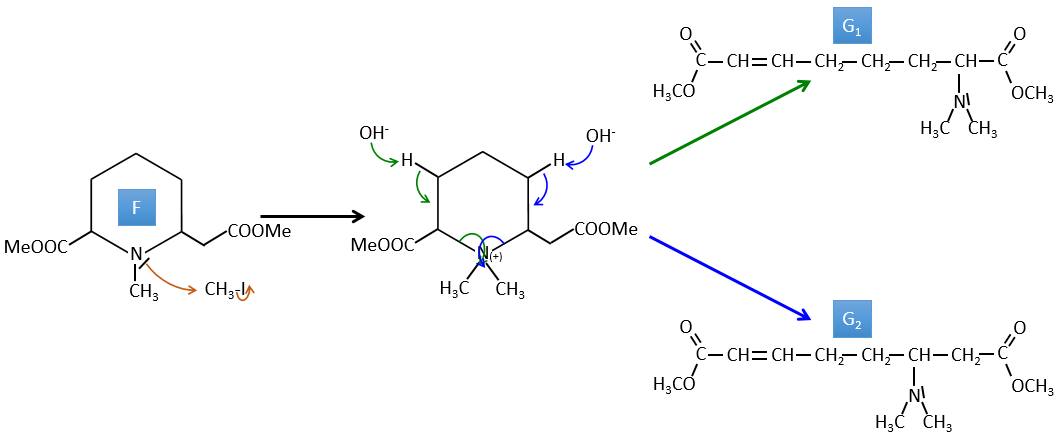
G→H: G1 and G2 are two isomers. There are two other information that we may consider to find the isomers. CH3I, Ag2O and delta are the reactants of the Hoffmann reaction. This reaction breaks one C-N bond and forms a double liaison on this carbon. It is thus one of the pi liaisons that the nitrogen was bound. The second information is that the nitrogen is no more on the product, meaning that it had only one liaison with the chain. The second product of the reaction, N(CH3)3, confirms that. The two isomers are thus different from the carbon on which N(CH3)2 was bound. It can be the carbon in α or in β of carbonyl.
F→G: It is the same reaction than G->H but the nitrogen is still on the molecule after the reaction. It means that it was bound somewhere else on the molecule. The location is where the pi liaison stands. The molecule had thus a cycle of 6 atoms prior to the reaction. Contrarily to the species H, the cycle F is not symmetric. It is why we can obtain two isomers G1 and G2.
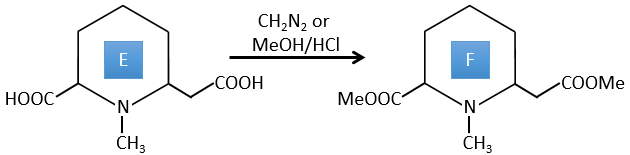
E→F: CH2N2 and MeOH/HCl are two techniques to replace a carboxylic acid by a methylic ester. The species E has thus two carboxylic acids.
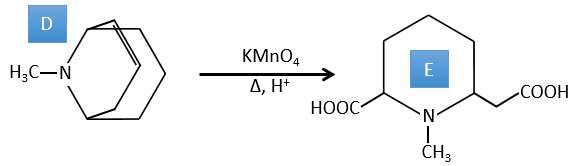
D→E: KMnO4 acts like the ozone. The two carboxylic acids were thus forming one bridge of the cycle. This bridge also forms a cycle of 6 atoms at the side of the nitrogen (and a cycle of 8 carbons with the other side).
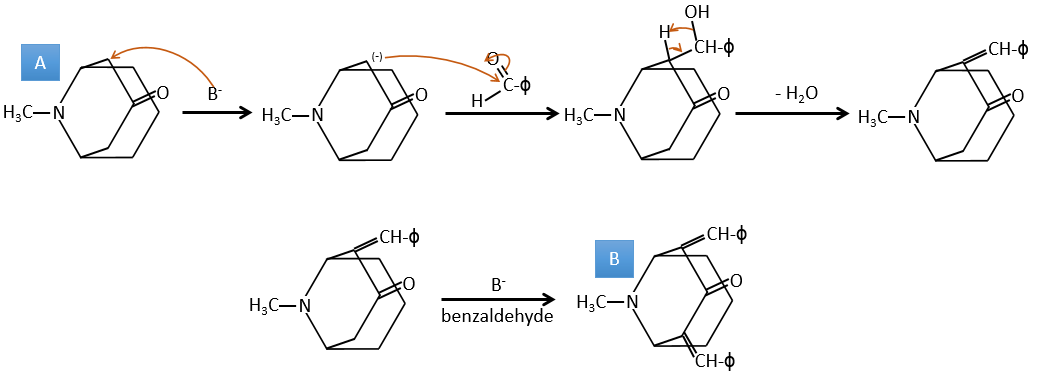
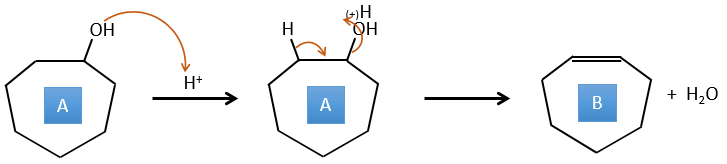
C→D: If we check the compositions of the reactant C and of the product D, we see that there is a difference of H2O. The role of H2SO4 was thus to remove this molecule of water from C with the formation of a double liaison. The hydroxyl group could be at two places (in α or β of the bridged carbons). At this point, we cannot say which position is correct but the reaction A->B is only possible with the hydroxyl group in β of the bridged carbon. The species is thus symmetric and achiral as is the species A.
A→C: A classic reaction of reduction. A gets H2 in the process and we can assume that the hydroxyl group was a ketone before the reduction.
A→B: The base is there to remove a proton in α of carbonyl. Those protons are acid in reason of the tautomerism enol-ketone. The carbanion attacks one benzaldehyde on its carbonyl and water is lost after this attack. The double liaison is in α of carbonyl and forms a long resonance chain with the phenyl. This reaction can be repeated on the other side of the carbonyl to obtain the product B.
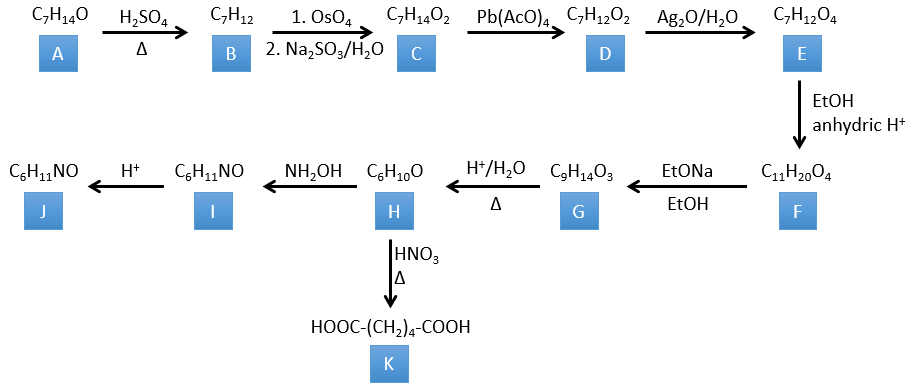
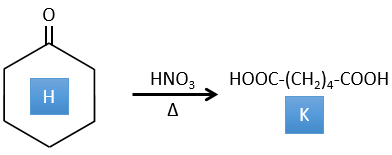
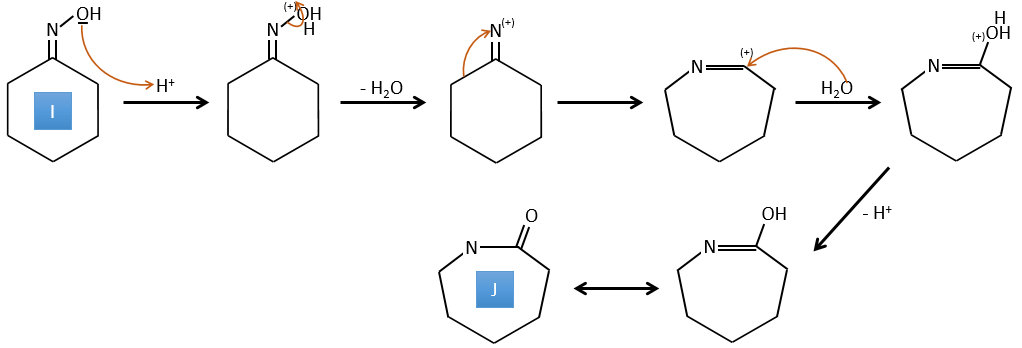
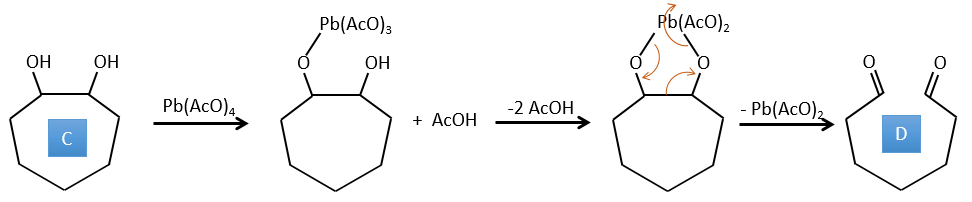
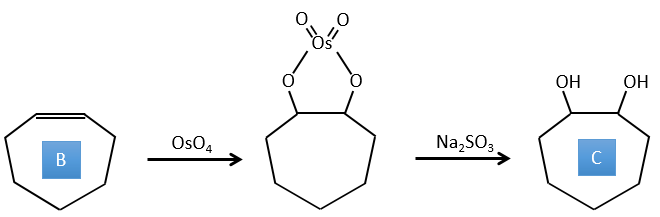
4. There are a few specific reactions in this exercise (mainly BàE). You have the formulas of all the compounds but only the structure of the compound K to start with. HNO3, ΔT is a reactant that breaks the C-C liaison of a ketone to obtain two carboxylic acids. The mechanism is unknown.
Correction
H→K: As explained in the wording, HNO3 breaks a ketone into two acids. As the two acids are present in the product, H is a cycle with a ketone on it. The cycle has 6 carbons.
H→I: This reaction leads to the formation of an oxime, i.e. a base of Schiff where R=OH. The mechanism involves a nucleophilic substitution by the nitrogen on the carbonyl to reject one water molecule.
I→J: This reaction is the transposition of Beckmann. Under acid conditions, the OH of the oxime is protonated and water is freed. The cationic nitrogen is attacked next by a carbon in alpha of the oxime, placing the nitrogen into the chain. The water comes back to attack the carbocation and to form an amide.
G→H: A simple reaction to change an ester into a carboxylic acid. The group is then removed from the molecule by an elevation of temperature.
F→G: A proton in α on carbonyl is taken by the strong base. The formed anion attacks next the ester to form a cycle of 6 carbons wearing one ketone and one methylic ester.

E→F: The carboxylic acids are replaced by methylic esters.
D→E: Ag2O is able to oxidize an aldehyde into a carboxylic acid.
C→D: Pb(AcO)4 is a compound that reacts with cis-glycols. Pb exchanges one equivalent of acetic acid to bind with one oxygen. The process is slow but it will also bind with the second OH to form a cycle of 5 atoms. This cycle breaks to generate 2 ketones that are now separated. The same mechanism is obtained with HIO4. As there is only one product, the he reactant is thus a cyclic cis-glycol.
B→C: The osmium tetroxide is a reactant that affects specifically C=C and that generates an osmic ester, a bit like the complex formed by Pb(AcO)4 with the cis-glycol. Na2SO3/H2O removes the osmium from the molecule to obtain the cis-diol. KMnO4 can do the same but we have to be in basic and cold conditions or we will obtain a diacid. The reactant is thus a cycle of 7 carbon with a double liaison between two of the carbons.
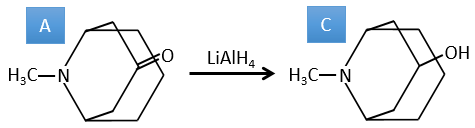
A→B: This reaction is simply the removal of a molecule of water from the cycle that gives a double liaison. We can deduce this from the difference of composition between the reactant and the product: C7H14O-C7H12=H2O.
Chapter 3 : Infrared spectroscopy
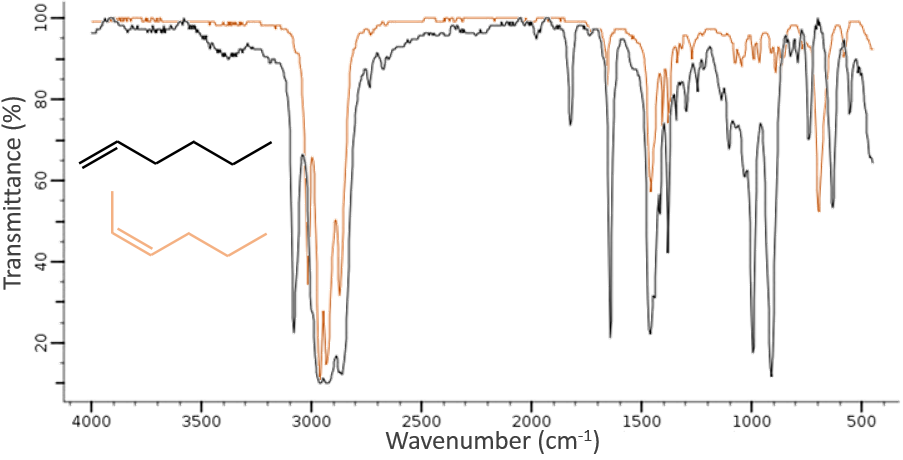
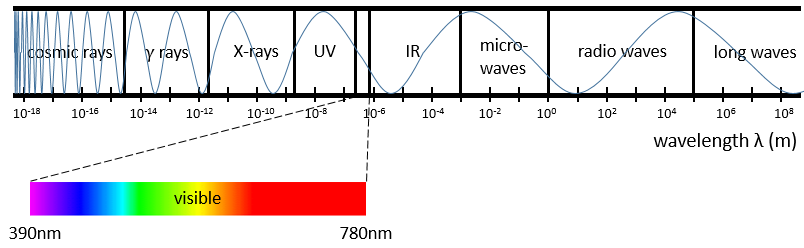
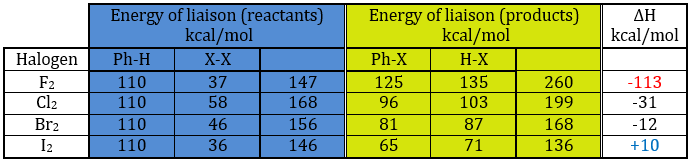
The IR spectroscopy has a different goal than the UV/visible. It is one of the strongest methods to determine the structure of organic compounds. An IR spectrum is similar to the finger print of one molecule and the matching of peaks can tell us if a molecule is in the sample or not. The spectrum showed below is the one of the 1-hexene in black and of the cis-2-hexene in orange. The difference of position of the double liaison leads to a huge difference in the IR spectrum.
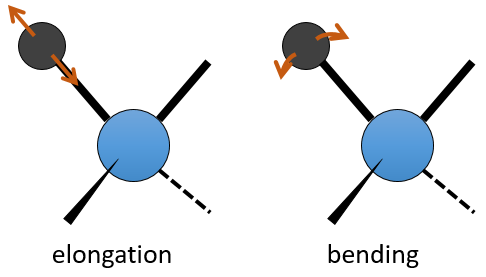
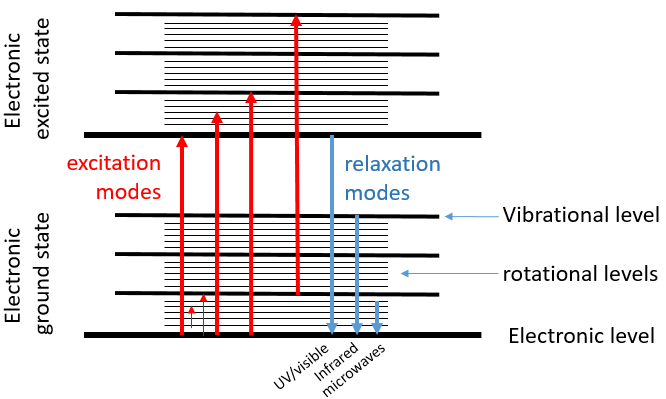
The UV/visible spectroscopy involves electronic transitions while the IR spectroscopy involves transitions between vibrational states. As for the UV/visible, we observe a series of bands, and not rays, because of the sublevel rotational states. There are two main modes of vibration: the elongation and the bending.
A liaison between two atoms has not a constant length. The atoms vibrate around their mass centre with a frequency that is characteristic of the pair of atoms. It is the elongation mode: a vibration in the axis of the liaison. However, the atoms are often bound to more than one other atom, modifying the frequency of the vibration and giving place to additional elongation processes.
The bending is a vibration out of the axis of the liaison. It leads to a variation of the angles between liaisons.
For a molecule of n atoms, the amount of degrees of liberty of the molecule is equal to the sum of the degrees of liberty of each atom. Each atom has 3 degrees of liberty corresponding to the 3 Cartesian coordinates required to describe its position in the molecule. The molecule has thus 3n degrees of liberty. Amongst the 3n, 3 are used to describe the translation modes and 3 are used to describe its rotation (2 if the molecule is linear). There are thus 3n-6 (or 3n-5) modes of vibration for each molecule. For instance, the water has 3 modes of vibration: 2 modes of elongation and 1 mode of bending.
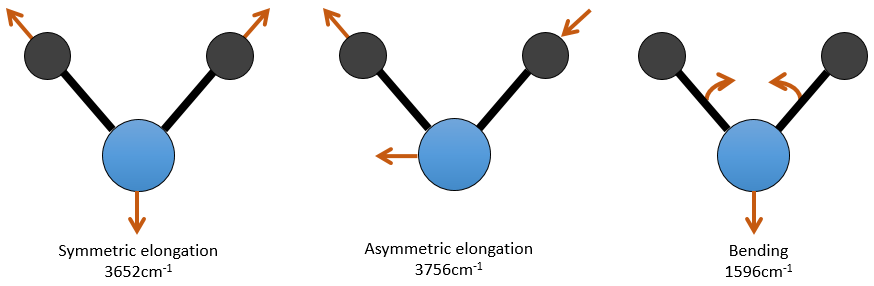
One mode of elongation is symmetric (the centre of mass is displaced) and one is asymmetric. Each mode shows a specific vibration, with a given wavelength. The wavelengths of the elongation modes are very close to each other and the bending mode has a smaller wavenumber. The fact that the elongation modes and the bending modes are distant in terms of wavelength and that the bending modes have smaller wavelengths are generalities that we can find for any liaison.
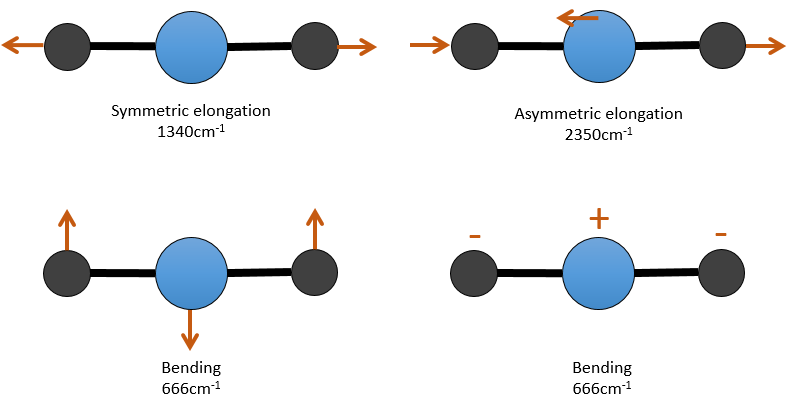
There are 3 atoms in the carbon dioxide but 4 modes of vibrations as the CO2 is linear (3n-5).
There is one symmetric and one asymmetric modes of elongation and two equivalent modes of bending (one in the x-y plane and one in the y-z). The bending modes have the same wavelength at 666cm-1. We say that those vibration modes are degenerated twice. Moreover, the symmetric elongation is inactive in IR because this mode of vibration does not induce any variation of the dipolar moment of the molecule.
In bigger molecules, it is rare to observe the exact number of modes of vibration (3n-6) because some modes come from combination from two vibrations or more, or are harmonics from strong modes of vibration. Those two effects increase the number of bands and other effects decrease this number
- bands that are too weak to be observed
- bands that are to close and that merge together
- degenerated bands
- inactive modes of vibration
- modes with wavenumbers out of the analysed range, usually between 4000 and 400cm-1.
It is possible to approximate the frequency of vibration of a given liaison with the law of Hooke that considers the liaison as a simple harmonic oscillator between two masses M1 and M2.
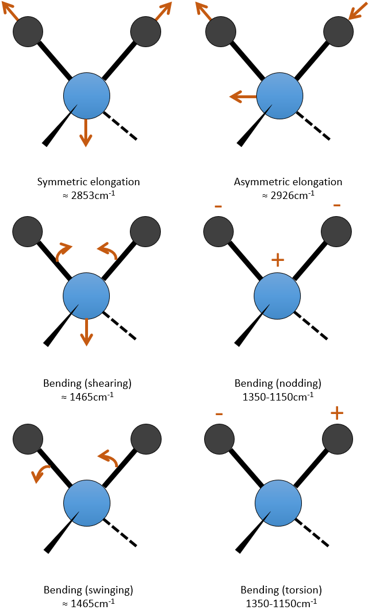
c is the speed of light and f is a constant that reflects the strength of the liaison, the value of which is approximately 5.105dyne/cm (1dyne=105N=105kg m s-2) for simple liaisons and two and three times this value for double and triple liaisons. f increases from left to right in the Mendeleev table. For instance, the law of Hooke gives a wavelength of 3040cm-1 for the C-H liaison. If we take a look to the vibration modes of CH2 inside a carbon chain, we find 6 modes of vibration (2 elongation modes and 4 bending modes).
Remember that the 3n-6 rule only applies to complete molecules. The elongation modes that we observe have frequencies that are a bit lower than the ones obtained by the law of Hooke (2926 and 2853cm-1 vs 3040cm-1) because of the environment of the C-H liaison that is not taken into account by Hooke.
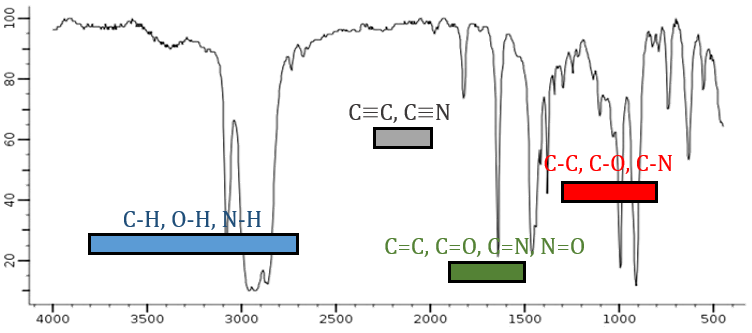
From the law of Hooke, it is obvious that heavy atoms vibrate at smaller frequencies. We can barely separate a IR spectrum in several regions depending on the pair of atoms involved in the liaison and the type of liaison:
| 3800-2700cm-1: C-H, O-H, N-H | 1900-1500cm-1: C=C, C=O, C=N, N=O |
| 2300-2000cm-1: C≡C, C≡N | 1300-800cm-1: C-C, C-O, C-N |
On the figure we can thus already deduce that there is no triple liaison (grey region) in our molecule (the 1-hexene from early), that there are some double liaisons (green region) and some simple liaisons (blue and red regions). However we cannot yet determine which peak corresponds to which vibration.
Coupled interactions
When two oscillators share a common atom, they rarely act as simple oscillators except if their vibrations modes are very different. The coupling between two modes of vibration produce two new modes of vibration with frequencies greater and smaller than the one in absence of interaction.
For instance, in the CO2, the asymmetric elongation (2350cm-1) and the symmetric elongation (1340cm-1) are the result of a coupling between the two C=O oscillations, one shortening when the other one elongates.
From what we have seen previously, one C=O should vibrate between 1900-1500 cm-1 but it is clearly not the case here. The coupling between the two C=O vibrations has for effect to displace the vibration towards larger frequencies (only the asymmetric is visible). The coupling becomes negligible when one or more carbons separate the liaisons. Two carbonyls separated by one or more carbons would show an absorption around 1725cm-1.
So the conditions to observe a coupling are that the vibrations share a common atom and have similar frequencies. However interactions are possible between fundamental vibrations and harmonic vibrations/vibrations of combination. Such coupling is called a resonance of Fermi. Still with the CO2, the symmetric elongation that is not active in IR but that can be observed in the Raman spectrum at 1340cm-1. In fact, there are two bands at 1286cm-1 and 1388cm-1 because of the coupling of the vibration with the harmonic of the bending modes (666cm-1). The first harmonic is thus at 1332cm-1 and interacts with the symmetric elongation mode at 1340cm-1.
Hydrogen bonds
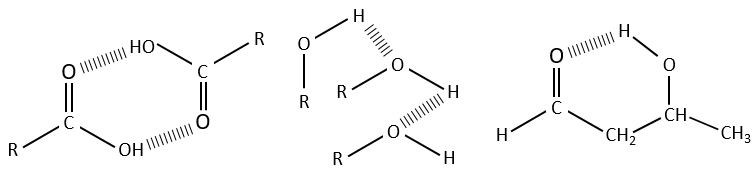
Hydrogen bonds decrease the frequencies of the involved liaisons and usually enlarge and enhance their bands. The importance of this effect depends on the strength of the H bond. A H bond is strong when it is in the exact direction of the lone pair of the electronegative atom. The strength of the bond also depends of the distance between the atoms, of the atom and if a cycle can be formed by the H bond.
The decrease of frequency varies from 300 to more than 500cm-1 if the H bond is intermolecular and from less than 100cm-1 to more than 300cm-1 if the bond is intramolecular. H bonds are often present between a molecule and the solvent. It is thus important to indicate the solvent and the concentration of the compound on a spectrum. The presence of water in the sample has a visible effect on spectra.
Analysis of a spectrum
An IR spectrum shows the transmittance as a function of the wavelength/wavenumber. The spectrum is to be read from top to bottom with bands dropping low in the spectrum.
An accurate analysis of an IR spectrum is not conceivable. The couplings, the absence of modes of vibration and the width of some bands make it difficult to determine the exact nature of the bands. However, as it has been said before, one IR spectrum is like the finger print of one compound and if one spectrum superimpose with the spectrum of a known molecule (with the same solvent, concentration and setup), the job is done. In other situations, an IR spectrum is used in combination with MS, UV and NMR spectra.
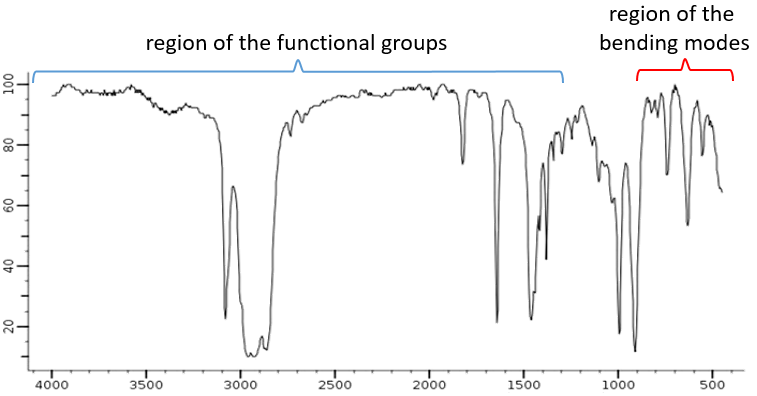
The spectrum, usually between 4000 and 400cm-1 can be split in two important regions to analyse: one between 4000 and 1300cm-1, called region of the functional groups, and one under 900cm-1 that shows the bending modes.
The elongation modes of functional groups with OH, NH, C=O can be found in the region of the functional groups. If this region is empty, we can assume that the molecule does not wear any of them. In rare situations, a weak and very wide band can be mistaken for an absence of band. Yet, be careful with low intensity bands that can also be harmonics or combination bands.
Characteristic absorbances
It would be too long to describe all the bands that can be observed on a IR spectrum. The goal here is more to give the very characteristic bands that can be easily spotted on the spectrum to have a general idea of what is in the molecule and what is not. In combination with a mass spectrum, it will be possible to determine the correct structure of the analysed molecule.
High frequencies vibrations
The region of the spectrum above 2850cm-1 is rich in information’s that can easily be studied. In this region we find the elongation bands of Y-H, Y=C, O, N. The bands are usually intense and are not hidden even if another band is nearby. The position of one band depends on the direct environment of the liaison. When necessary, we write this liaison (simple, double or triple) to demark =C-H, i.e. a hydrogen bond to a carbon with a double liaison, from –C-H for instance, i.e. a hydrogen bond to a carbon with a simple liaison.
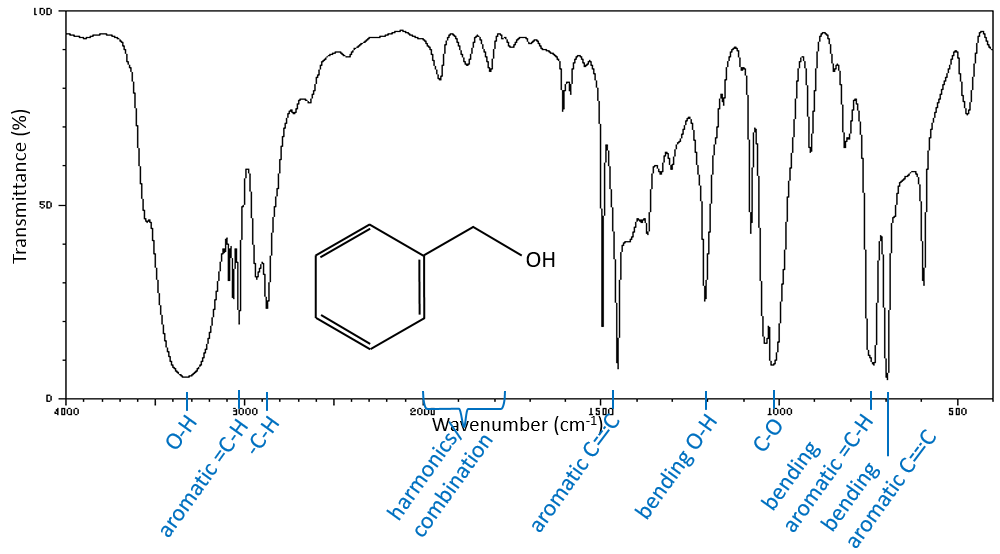
A first hint on the nature of the compound is found in the vicinity of 3000cm-1 where the C-H liaisons absorb. The difference of frequency between aromatic =C-H and aliphatic -C-H is small but is characteristic:
Methylic C-H are found as 2 bands at 2962cm-1 and 2872cm-1 and methylenic C-H are found a bit lower (2926 and 2853cm-1). =C-H are found slightly above 3000cm-1. It is often synonym of an aromatic but is can also simply be an alkene (or conjugated double liaisons). On the spectrum of the hexene, the peak at 3080cm-1 is characteristic of the double liaison and the peaks for the –C-H are hidden in the large cluster. Three small peaks are however visible around the values cited above for Methylic and methylenic –C-H.
It is thus easy to guess the presence of an aromatic cycle from the –C-H bands but it is not easy to determine if the =C-H absorbance band come from an aromatic or an alkene: both alkene =C-H and aromatic =C-H show an intense band in the low frequencies region, respectively between 1000-650cm-1 and 900-675cm-1. The aromatics (and heteroaromatics) will also show 3 peaks around 1600cm-1, 1500-1400cm-1 and 1300-1000cm-1 (note that conjugated alkene also show that kind of bands). Still in the spectrum of the hexene, the peak between 1300 and 1000cm-1 is not present and the bending peak is lower than 675cm-1.
The C-H bond of aldehydes vibrates at smaller wavenumbers, between 2830 and 2695cm-1 because the carbonyl takes electrons from the C-H and this liaison is thus longer, making it vibrate slower. The peak is not very intense and can be doubled because of a resonance of Fermi with the first harmonic of the bending mode at 1390cm-1.
≡C-H bond to triple liaisons are absorbing at frequencies above 3100cm-1, between 3333cm-1 (this one is easy to remember) and 3267cm-1 but are not the single species absorbing above 3100cm-1. We can also find –O-H and N-H elongation bands as well as H bonds. The ≡C-H bands are usually thinner than the bands for –O-H and –N-H and are intense.
-O-H elongation bands
The –O-H bands are large and intense, and very large in the case of carboxylic acids. In fact, those large bands are the result of the H bonds and the formation of dimers when the concentration of alcohol/acid are much diluted.
Free –O-H give small and thin bands between 3650 and 3584cm-1 for alcohols and around 3550cm-1 for acids but are easily erased by the large bands of H:O-H that are spreading over hundreds of cm-1 are way more intense. Those large bands should be centred between 3550 and 3200cm-1 (for the benzyl alcohol it is at 3320cm-1) for alcohols and 3000cm-1 for acids.
-N-H elongation bands
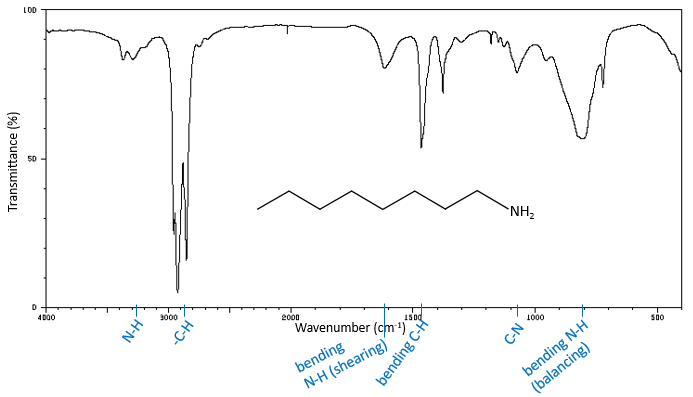
The high frequencies bands for aliphatic amines are quite weak between 3400 and 3250cm-1. There are two bands in the case of primary amines and 1 band in the case of secondary amine. The N-H elongation modes are slightly displaced towards larger frequencies if the amine is aromatic. The spectrum is different in the case of amine salts. Ammonium ions give a large and intense band of absorption between 3300 and 3030cm-1. The frequency decreases with the degree of the amine: primary amine: 3000-2800cm-1, secondary amines: 3000-2700cm-1, tertiary amine: 2700-2250cm-1).
In absence of H bond, the primary amide shows two bands around 3520 and 3400cm-1 while secondary amides show one band of absorbance between 3500 and 3400cm-1. In more concentrated solutions or in solids, H bonds displace the bands towards smaller frequencies, respectively around 3350 and 3180cm-1 for primary amides and multiple bands between 3330 and 3060cm-1 for secondary amides. The presence of multiple bands instead of one single band is explained by the formation of a dimmer of amides.
Middle range frequencies
Between 2850 and 900cm-1, we can find bands characteristic of elongation vibrations between two atoms other than H and some bending vibrations of Y-H that can confirm the observations from the high frequencies region of the IR spectrum. We will focus on the elongation bands.
The S-H liaisons produce a small band of absorption between 2600 and 2550cm-1. This band is lonely in this region of the spectrum but in diluted solutions the band can be to small to be detected.
C≡C shows a small band of absorbance between 2260 and 2100cm-1. This region is dedicated to triple liaisons (C≡N shows a band between 2260 and 2240cm-1) but harmonics and combination bands can be found in this region too. The bands of C=C are or middle or weak intensity between 1667 and 1640cm-1 for alkenes that are not conjugated. Those alkenes are found between 1650 and 1600cm-1. The cumulated alkenes (c=c=c) absorb between 2000 and 1900cm-1.
Elongation vibrations of C=O
The absence of absorbance between 1870 and 1540cm-1 is synonym of the absence of carbonyl. In this region, the position of the peak depend on the conjugation of the carbonyl and of the substituents (which substituent and its mass) and the possible H bonds.
An aliphatic ketone is found at 1715cm-1. Modifications of the environment of the ketone can induce either an increase of a decrease of the wavenumber of the peak that depends on the predominance of the inductive or of the resonance effect. The inductive effect reduces the length of the C=O liaison, leading to the increase of its frequency of vibration. A resonance increases the length of the C=O liaison, displacing the peak towards the C-O peak that is at a lower frequency. For instance, Cl has a predominant inductive effect and the peak of the C=O is at 1815-1785cm-1. The carbonyl of a primary amide vibrates at 1695-1650cm-1 because the resonance effect is predominant. There are two bands for primary amides and only one for the other ones. Carbonyls conjugated with alkenes have peaks of absorption at smaller wavenumbers than the aliphatic ketone between 1685 and 1666cm-1. An aldehyde absorbs a bit higher than the ketone (1740-1720cm-1). An acid absorbs strongly (way more intensely than a ketone) around 1760cm-1 but H bonds in dimmers of acids can displace the peak towards smaller frequencies (1720-1706cm-1). Esters absorb at 1750-1735cm-1. An acyl halide shows a strong absorption between 1815 and 1785cm-1.
H bonds decrease the frequency of vibration of the carbonyls. The effect is small for intermolecular H bonds (a dozen of cm-1) but can be important for intramolecular H bonds.
Elongation vibrations of C-O
In the middle range spectrum, between 1300 and 900cm-1 the spectrum is usually complicated. It is the “digital print” of the compound where we can find the bands of alcohols C-C-O that should be accompanied with O-H bands at large frequencies.
The C-O liaison of alcohols shows an intense band due to the vibrations of elongation between 1260 and 1000cm-1. This mode of vibration is usually coupled with the next carbon, as an asymmetric elongation C-C-O. The C-O-C of ethers and epoxides systems can also be found in this region of the spectrum, between 1150 and 1086cm-1 (for its asymmetric elongation, the symmetric being very weak because it does not modify the dipolar moment) as an intense band or several bands if the nearby carbons are ramified. If one side is an aryl group, we observe one intense band (asymmetric elongation) at 1275-1200cm-1 and one intense band (symmetric elongation) at 1075-1020cm-1). Finally, the vinyl ethers show similar bands (1225-1200cm-1 and 1075-1020cm-1).
Acids give two bands of in unequal intensities, in addition of the one of C=O, coming from an interaction between the elongation mode of C-O and the bending mode of O-H. We talk about the bands of C-O-H. The most intense band between 1315 and 1280cm-1 is called the elongation band C-O. The second band, between 1440 and 1395cm-1 is the band called the band of bending O-H. This band falls in the same region than the shearing mode of CH2. The carboxylate also gives two bands of unequal intensities, the most intense one between 1650 and 1550cm-1 and the other one around 1400cm-1.
A particularity of the esters is their intense band of absorption at the place of the elongation mode of the ketones. This band is not the band of C=O, that is displaced towards larger frequencies but one of the two bands of C-O. The C=O band is indeed between 1750 and 1735cm-1 and 20cm-1 lower if the carbonyl is conjugated. The C-O vibration is coupled with both sides of the liaison, leading to two bands of absorption. The most intense one is C-C(=O)-O giving a peak between 1300 and 1000cm-1. Esters of aromatic acids absorb strongly between 1310 and 1250cm-1. The other band between 1111 and 1031cm-1 comes from the coupling O-C-C. Its frequency depends on the substituent of the ester. Esters of primary alcohols are at the lowest frequencies (1064-1031cm-1) while esters of secondary alcohols and of aromatics absorb around 1100cm-1and 1111cm-1 respectively.
Elongation vibrations of NO
Nitro groups have a symmetric and an asymmetric elongation mode of vibration. The asymmetric mode gives an intense band between 1661 and 1499cm-1. The symmetric mode gives a band between 1389 and 1259cm-1. The wavenumbers of both bands depend on the substituent of the nitro group. In the case of an alkane, the bands should be observed around 1550 and 1372cm-1 respectively. An electronegative group on the alpha carbon increases the frequency while a conjugation decreases the frequency.
Nitrates show 2 intense bands of elongation for N=O (one asymmetric and one symmetric) between 1300-1255cm-1 and 1660-1625cm-1. Nitrites have two bands as well, one for the cis (1625-1610cm-1) and one for the trans isomer (1680-1650cm-1).
Nitroso compounds show an absorption band between 1585 and 1539cm-1.
Elongation modes of C=S
The elongation modes of C-S are found in the low frequencies range and the C=S slightly above this region, between 1250 and 1020cm-1. This band is less intense than the one of a C=O because it is less polar.
Elongation modes of S=O
The S=O liaisons produce intense bands in general. The S=O liaison of sulfoxides vibrates between 1070 and 1030cm-1. Sulfones show two bands of absorption between 1350-1300cm-1 and 1160-1120cm-1. The bands are displaced towards larger frequencies in the case of a sulfonyl chloride (1410-1380cm-1 and 1204-1177cm-1) or of a sulfonamide (1370-1335cm-1 and 1170-1155cm-1).
Bending in the middle range region
Several liaisons with elongation modes of high frequency, typically Y-H liaisons, have bending modes that fall in the same region than other elongation modes (Y-Z). They complicate the reading of the spectrum but can also confirm peaks of the high frequencies region.
C-H bending modes
The bending modes of the methylenic C-H liaisons have been seen at the beginning of this chapter. One mode is in the low frequencies region at 720cm-1 and the three other are in the middle range region. The shearing mode has an almost fixed wavenumber of 1465cm-1 but the two last modes (nod and torsion) give peaks between 1350 and 1150cm-1. In a cycle, those frequencies are slightly decreased. Methylic C-H have two bending modes: one where the three H oscillate in phase and one wherein one H is not in phase. The symmetric mode (in phase) gives a peak at 1375cm-1 and the asymmetric mode at 1450cm-1, almost at the same frequency than the shearing mode of a methylenic C-H. =C-H of alkenes absorb at 1415cm-1 due to a shearing mode. Aromatics have a mode of bending out of the plane that give intense peaks in the low frequencies region and a bending mode in the plane give peaks between 1300 and 1000cm-1.
Bending O-H
Peaks of alcohols are not very characteristic and are in the region between 1420 and 1330cm-1. If there is a proton on the carbon wearing the –OH (i.e. primary and secondary alcohols), there is a coupling that gives two bands around 1420 and 1330cm-1. Tertiary alcohols give only one peak. In the case of the acids, there is an interaction between the elongation mode of C-O and the bending mode of O-H (discussed in the C-O elongation modes section). The C-O-H bending mode should be found between 1440cm-1 and 1395cm-1.
Bending N-H
Primary amines have a bending mode that gives a peak of average to high intensity between 1650cm-1 and 1580cm-1. The bending mode of secondary amines is hardly detectable except for aromatic secondary amines that absorb around 1515cm-1. In the case of amides, the N-H bending mode should be observed by a band between 1655 and 1590cm-1 with an intensity way smaller than the intensity of the C=O peak. As C=O absorbs in the same region, the peaks of the elongation C=O and of the bending N-H can merge.
Low frequencies region
In this region we find mostly the bending modes but some elongation modes are also present. In my opinion, this region is less interesting than the high and middle frequencies regions and is pretty hard to read because several modes have large ranges of possible frequencies that overlap with other modes. The most characteristic peaks are the peaks for dimmers and for aromatics. Between 900 and 650cm-1, a large and intense band is characteristic of a dimmer of acid, amide or amine. In the same region, the absence of intense peaks indicates that the molecule is not an aromatic.
Bending modes of CH
The peak of the swinging mode of methylenic -C-H at 720cm-1 has a low intensity or is not visible. A very intense band (usually the most intense of the spectrum) is visible between 1000 and 650cm-1 if an alkene is present in the molecule, coming from a bending mode out of the plane. It is usually this kind of bending out of the plane that gives intense bands in the low frequencies region. A very intense peak can thus be observed for aromatics between 900 and 650cm-1. The alkynes give a thick and intense peak at lower frequencies, between 700 and 610cm-1.
Other bending modes
The bending mode of alcohols gives a thick peak between 769cm-1 and 650cm-1 in addition of the bending modes of the middle frequencies region. Dimers of acids give a very broad band (not as large as the band in high frequencies that the acids give but it is characteristic) of average intensity centred near 920cm-1. Amides also give a thick band of average intensity but between 800 and 666cm-1, again due to a bending out of the plane. This bending is stronger and at higher frequencies for amines (909-666cm-1).
The bending out of the plane of the amines and amides generate one average/intense band respectively between 909-666cm-1 and 800-666cm-1. Nitro groups seem to show a bending mode between 763 and 690cm-1.
Elongation modes in the low frequencies region
A band of elongation of N-O appears between 870-833cm-1 from nitro groups and between 850-750cm-1 from nitrites. C-S absorbs between 700 and 600cm-1.
Finally, halogens have their elongations modes in the low frequencies. In an aliphatic chain, C-Cl absorbs between 850 and 550cm-1, C-Br between 690 and 515cm-1, C-I between 600 and 500cm-1 and C-F between 1400 and 730cm-1. The band of C-F is strong and large. If the substituent is an aromatic, the bands are displaced towards larger frequencies, above 1000cm-1 in the case of chlorobenzenes.
Chapter 2 : Spectroscopic methods
Spectroscopic methods are destined to determine the composition of samples containing one or several species on the basis of their energy levels. We have seen that the electrons of atoms don’t have access to any value of energy. They are limited to a few values of energy, the energy orbital’s/levels 1s, 2s, 2p, etc, on which they are distributed following the rule of Fermi, beginning with the energy levels with lowest energies and filling the levels until there are no more electron to place.
The electrons of highest energy can be excited and reach orbitals of higher energies if they receive the exact amount of energy ΔE separating the two energy levels, in the form of heat of or photons. We say that the electron passes from its ground state to an excited state.
When an excited electron goes back to its ground state, it generates a photon with the same energy ΔE=hν. The frequency of the photon is characteristic of the atom or of the molecule from which it is emitted. The frequency ν, as a unit of measure, is the amount of times that a process occurs over a period of one second. In the case of photons, it is the amount of waves that passes by a point over one second (units: hertz). The wavelength λ=c/ν is the length of one wave, or the distance between two summits, in meter. The wavenumber n is the reciprocal of the wavelength (1/λ, units: cm-1). The difference between the frequency and the wavenumber is that wavenumber has nothing to do with the velocity of the wave. This makes it useful for situations where the velocity or frequency are not fixed.
For instance, when we heat up a metal, it changes of colour because the excited electrons emit photons within the range of the visible. The spectre of the visible is composed of all the colours that humans can see. Each colour corresponds to a photon of a given wavelength. The violet is the visible colour with the smallest wavelength (390nm) (or the largest wavenumber) and the red is the visible colour that has the largest wavelength (780nm) (or the smallest wavenumber). Ironically the colour that we see on a given material is not the colour that the material absorbs but all the other colours that haven’t been absorbed and that are thus reflected by the material towards our eye.
Radiations are not limited to the visible spectre. There are photons with wavelength above 780nm and below 390nm. Radiations with a wavenumber smaller than the visible spectre are called infrared (the red being the colour with the smallest wavenumber). If we continue to decrease the wavenumber (or increase the wavelength) we reach the microwaves and then the radio waves. On the other side of the visible spectre we find the ultraviolet radiations (the violet having the largest wavenumber of the visible spectre), then the X-rays and finally the γ-rays. As the energy of a photon is E=hν, the photons gain energy when we go from the radio waves towards the gamma rays. X-rays have enough energy to extract a deep electron (not an electron of valence) from an atom. No need to say the damages that gammas rays from radioactive elements can do.
The electronic transitions we discussed previously correspond to radiations in the UV/visible spectre. Those transitions are not the only transitions that can take place. Between each electronic level we find vibration levels and between the vibration levels we find rotational levels. The transitions between vibration levels are in the range of the IR while rotational transitions are in the range of the microwaves. These transitions lead to an emission of heat and that’s exactly how the microwaves oven works: the food is bombarded by radiations in the range of microwaves and the molecules of the food rotate, generating the heating of the food.
Spectroscopy
The absorption of radiations of a solution depends thus on its composition. We can whether measure how a solution absorbs a given radiation or how this solution emits photons when its molecules are excited.
Absorption spectroscopy
The absorbance A of a solution is its capacity to block/absorb radiations. The absorbance A(λ) depends on the wavelength of the radiation.
If we consider an incoming ray with an intensity I0 that is heading towards a cell of length b containing a solution with a concentration c, the intensity I of the ray behind the cell is decreased by dI proportionally to the length of the cell (a longer cell absorbs more) and to the concentration of the solution (a more concentrated solution absorbs more).
E is the coefficient of absorbance of the solution that does not depends on the concentration nor on the size of the cell and dc is the concentration of solution through which the ray passed through, i.e. the difference of concentration between inside and outside the cell. We can rewrite this expression as
and we can integer dI and dc between the emission of the ray and its detection, i.e. from I=I0 to I=I and from c=0 to c=c. It gives
The absorbance is thus given by the law of Beer-Lambert
We can also define the transmittance that is T=I/I0.
The absorbance is thus directly proportional to the concentration of the solution. Deviations from the linearity can be observed for concentrated solutions (c≠activity) or if some molecules of the sample are involved in an equilibrium.
The walls of the cell are made to let a maximum of the ray pass. They are usually in quartz (transparent between 200 and 380nm). A variation of the intensity of the ray can however be observed but can be determined using a white solution, i.e. a solution that only contain the solvent, with c=0 or a reference. The detector can be setup to define T=1 (or A=0) with the white solution. As the absorbance is directly proportional to the concentration of the solution we can determine the concentration of our sample if we measured the absorbance of our white solution and of an etalon solution the concentration of which is known.
If several species are in the solution, the absorbance is the sum of the individual absorbances.
To determine the concentrations, we need to repeat the experiment at several wavelengths. Don’t forget that epsilon depends on the wavelength.
We can thus determine c1 and c2 if the εi are known.
Experimental setup
The instrument is composed of 5 major parts:
- A stable source of radiant energy,
- A transparent device destined to contain the sample,
- A system to select a range of the spectre,
- A detector that can transform the luminous signal into an electric signal,
- A device to treat the signal.
The source of the ray has to be a monochromatic lamp, sending only photons with a given wavelength. It can be for instance a hollow cathode lamp or a laser source. However, there is always a small range of wavelengths that is emitted. The impact can be limited if the wavelength is so that the ε coefficients don’t vary too much on this range of wavelengths.
The cell is usually in quartz and its size is usually 1cm long for spectroscopy of solutions. For gases the thickness is between 1 and 100mm but the ray can pass several times in the cell with the use of mirrors, giving optical paths up to 120m. It is also possible to allow a flow of gas.
The selection of the wavelength is done by a combination of prisms/mirrors and thin gaps. The prisms separate the wavelengths of the incident light and the gaps only allow a small range of wavelengths to pass toward the detector.
The detector can also introduce some error in the measure. The relative intensity of those errors is large when A→0 or when it A is large. Again, a good choice of wavelength limits the experimental errors.
Molecular spectroscopy
Another way to use the absorption properties of solutions is to sweep a range of wavelengths and to detect the absorbance. It requires a source of light able to change of wavelength. If there were only the electronic levels, we would obtain discrete rays corresponding to the exact energy of the transition between the ground state of the electron and one excited state. However, the rotational and vibrational sublevels transform the rays into bands. The bands are thinned if we perform the spectroscopy of gases. In the case of UV-visible absorption spectroscopy, this technique is mostly used quantitatively. For instance we can follow the evolution of a reaction through the spectre of absorbance. If the products and the reactants are absorbing at different wavelengths, the intensity of the peaks characteristic of the products will increase over time while the peaks of the reactants decrease in size.
Chromophore: it is an organic covalent unsaturated group that absorbs in the UV (ex: C=C, C=O, NO2) with electrons that can be delocalised. The photons excite electrons that jump between energy levels that are extended π orbitals, created by a series of alternating single and double bonds, often in aromatic systems.
Auxochrome: A saturated group with free electrons that modifies the intensity and the wavelength of the absorption when bound to a chromophore.
Bathochromic shift: displacement of the absorption towards larger wavelengths (displacement towards the red) due to a solvent effect or a substitution.
Hypsochromic shift: displacement of the absorption towards smaller wavelengths (displacement towards the blue) due to a solvent effect or a substitution.
Hyperchromicity: increase of the intensity of the absorption.
Hypochromicity: decrease of the intensity of the absorption.
Chapter 1: Reactions of substitution on aromatic cycles
Aromatic cycles, such as the benzene, are very stable because of their energy of resonance. As a result, it is very difficult to “open” the cycle by an usual reaction of addition.
Instead of addition reactions, we observe reactions of substitution. The mechanism involves two steps.
- the first step is the electrophile attack of one pi liaison on an electrophile. As this step implies the loss of aromaticity of the substrate, this step is slow and is the determining step of the reaction. The product of this step is called an intermediate of Wheland or an arenium ion.
- the second step involves the removal of a proton from the cycle to regenerate the aromaticity. This step is fast.
Most of the electrophiles have to be activated to allow the first step of the reaction. It is done by a Lewis acid.
Halogenation
FeBr3 and AlCl3 can be used as Lewis acids to bind a halogen (Br and Cl respectively) on a benzene ring.
They enhance the electrophile character of the halogen that can now be attacked by the aromatic substrate.
FeBr4– acts like a base to take a proton and close the ring.
In the following table, we can find the energies of liaison involved in the process for the halogens. On the left, we have the energies for the reactants and in the middle column we have the energies for the products. The enthalpy of reaction is shown on the right column.
If we take a look at the variation of energy involved by a halogenation, we see that the enthalpy of reaction is positive for iodine. The reaction is thus not done. The reaction is highly exothermic for F2. In fact, this reaction is explosive. For Cl and Br, we need to use catalysts (the Lewis acids).
Sulfonation and nitration
SO3 and NO2+ are electrophile enough to bind with an aromatic ring.
The nitrate can be reduced selectively to obtain an amine.
Sulfonation
The sulphur atom is electrophile because of the electrocaptor character of the oxygen’s. However, the reaction is reversible in presence of water to form sulphuric acid. This process is exothermic and we should keep an eye on it.
We produce detergents from the benzenesulfonic acid.
And from that point we can produce sulfonamides that are usually good antibiotics.
The first of this kind was the Prontosil (4-[(2,4-Diaminophenyl)azo]benzenesulfonamide) in 1932, developed by Domagk at Bayer, who won a Nobel prize in medicine for it in 1939. The research program was designed to find dyes that might act as antibacterial drugs in the body. The discovery and development of this first sulfonamide drug opened a new era in medicine. Other examples of antibacterial agents follow:
Alkylation of Friedel-Crafts
This reaction, as its name mentions, allows to bind a chain on an aromatic ring. The chain that is to be added has to have an electrophile carbon. Again, we need a Lewis acid to do this reaction. The first step is the activation of the halogenoalkane by the Lewis acid.
Next, the cycle attacks the alkane, ejecting the halogenated Lewis acid. The product of this step is called an intermediate of Wheland or an arenium ion. This step is the determining step of the reaction, involving the opening of the ring due to the electrophile attack. A proton is taken by the halogenated Lewis acid to give the aromaticity back with the recovering of the Lewis acid and the liberation of an acid. This step is fast with regard to the previous step. As a global result, we added a new carbon chain on the phenyl.
The halogen on the added chain is not mandatory. An alcohol can do the job as well, or other precursors of carbocations.
The alkylation can be intramolecular if it results in a new cycle.
Limitations of the method
The alkyl group that has been added to the phenyl is an inductive donor group. It means that it gives some of its charge to the phenyl, increasing its ability to attack electrophilic carbons. As a result, the alkylation process does not stop after the addition of one chain if there is still places on the phenyl to greet new ones (we will see a bit later on which spot which group can be added).
A second limitation is the rearrangement of the carbocation (as usual).
Acylation of Friedel-Crafts
The difference between the alkylation and the acylation is that for the second one the electrophile is an acylium cation, leading to the addition of -C=O-R on the phenyl.
The acylium ion is obtained with the help on a Lewis acid
The rest of the process is identical.
However, there is no polyacylation because the carbonyl is a mesomeric and inductive captor, taking electrons from the cycle. It is possible to reduce the ketone with the reaction of Clemmensen or of Wolff-Kishner.
Regioselectivity
A benzene that already wears a group can be attacked on 3 non-equivalent positions: the ortho, meta and para positions. Some groups orient the reaction towards the ortho/para positions and other groups towards the meta position.
Mesomer effect
The mesomeric effect is the possibility for a heteroatom to share one lone pair with nearby atoms. For instance, O and N are mesomeric donors. They can stabilise carbocations by the sharing of one of their lone pairs that counterbalances the positive charge. They also enhance the nucleophile character of double liaisons. We note the mesomeric donors +M.
Groups can also be mesomeric acceptors and are noted –M. For instance the NO2 group is a mesomeric acceptor because it has a resonance form that can keep the additional charge.
Note that the oxygen can be mesomeric donor or acceptor depending on the group it is in and of the structure of the molecule.
Inductive effect
When two atoms are of different electronegativity, there is a displacement of electrons from the least electronegative atom to the most electronegative one. Groups or atoms can thus take or give some electrons from or to the nearby atoms. Atoms or groups that take electrons from the rest of the molecule are inductive acceptors and are noted –I. They destabilise carbocations and positive charge and can enhance the electrophile character of the atom they are bond with. For instance, the carbon of a carbonyl give a part of its charge to the oxygen and wears a partial positive charge δ+. A nucleophile is thus prone to attack this carbon.
An atom that is less electronegative than the carbon will give a part of its charge to the chain. They are called inductive donors and noted +I. The simplest inductive donor is H that is less electronegative than the carbon. However, H is taken by convention as the neutral intensity of the inductive effect. –CH3 is an inductive donor because the inductive effect of the 3 hydrogen’s is transmitted through the carbonic chain (over 2-3 carbons). As a result, the alkyl groups are inductive donors. The effect is stronger for -C(CH3)3 than for –CH3 because the amount of hydrogen atoms that can share their electrons.
The hybridation of the carbon is something to be taken into account to determine the inductive effect. The electrons in the s orbitals are more bound to the atom than the ones from the p orbitals. As a result, the electronegativity of sp2 carbons is slightly higher than the electronegativity of sp3 carbons.
Regioselectivity in function of the substituents of aromatic rings
The mesomeric and inductive effects are cumulative and a nitrogen in a NH2 group is simultaneously a mesomeric donor and inductive acceptor (+I-M). The mesomeric effect always prevails in intensity.
- inductive donors
The groups that are donors of electron by hyperconjugaison (or inductive donors) are activating, i.e. favour the addition of new groups on the carbon. The substitution is oriented towards the ortho and para positions because the carbocation which has been made during the first step of the substitution can be stabilised by the inductive donor.
It is not possible to place the positive charge on the spot of the group if the substitution was to be made on the meta position. Usually, the para position is favoured to the ortho position because of the steric hindrance. However some groups such as NO2 seem to show more interest on the ortho position.
- inductive captors
Inductive electrocaptors are deactivating and orientate the reaction in meta. The reason is that in the other two positions, the carbocation can be at the feet of the CF3 group that wants to take more electrons, destabilizing furthermore the carbocation.
- mesomeric donors
Mesomeric electrodonors are activating and orientate the reaction in ortho/para because there is an additional resonance form.
Note that NH2, as well as the oxygen from the ether, is a mesomeric donor and an inductive captor. The mesomeric effect is always more important than the inductive one.
- mesomeric captors
Groups that are electrocaptor by resonance are deactivating and orient the reaction in meta.
- halogens
Halogens are deactivating but orient the reaction in ortho and para.
The steric hindrance here is very important and explain the difference of population between the ortho and para reactions.
If there were two groups on the phenyl, the effects are additive and the substitution is made on the most activated/ less deactivated positions.
Both methyl groups of the xylene (dimehtylbenzene) shown above are activating and orientate in ortho/para. As both groups are activating, this reactant is more reactive than the toluene. The positions 2, 4 et 6 are thus favoured. The positions 4 and 6 are slightly more probable because there is less steric hindrance. In the case of the following xylene, the slots are almost equivalent.
In the case of deactivating groups, the same reflexion is made. The COOH’s orientate in meta and the position 5 is the least deactivated position.
Nucleophilic substitutions
The nucleophilic substitution on aromatic rings is slower than the electrophilic substitution and that substitutions on sp3 carbons.
The reason is that the cycle is already full of electrons. Moreover, a sp2 carbon is more electronegative than a sp3 carbon. It is thus difficult to add a nucleophile (that loves positive charges) on a phenyl and the presence of a captor group on the phenyl is required to stabilise the carbanion. The leaving group has to be a good one.
Several mechanism are possible to add a nucleophile on an aromatic substrate. One of them is the Addition-Elimination.
The activating group (NO2 here), is necessary to stabilise the negative charge of the carbanion formed during the first step of the reaction which is the slowest one. The intermediate complex is called intermediate complex of Meisenheimer.
The halogen (as leaving group) reactivity sequence is opposite to the one for SN2. On an aliphatic chain, the cleavage of the C-X liaison is made during the determining step of the SN2. On an aromatic, the cleavage doesn’t take place during the determining step. Moreover, the halogens take electrons from the cycle and the small halogens are thus more reactive than the big ones. As a result, we have the following reactivity sequences:
Aliphatic: F<<Cl<Br<I
Aromatic: F>>Cl>Br>I
A heterogeneous atom in the cycle (O or N) can play the role of the captor group.
An application of this mechanism is the determination of the terminal amino acid of peptides. The peptide reacts with an aromatic compound through its terminal amine group.
Once the two substrates are bound together, we hydrolyse the peptide bonds (i.e. the amides). All the amino acids are now separated but only one of them is bound to the aromatic group.
SN1 mechanism
This mechanism is mostly used to produce salts of arenediazonium. This species is obtained from aniline C6H7N with NaNO2 in an acidic environment.
The mechanism is the following:
Arenediazonium salts are stables at low temperatures and lose N2 at higher temperatures, freeing a phenyl cation that can react with a nucleophile.
Other halogens than iodine don’t give good results because of secondary reactions. To add Cl, Br or F on an aromatic cycle, we use the Sandmeyer reaction, using copper salts like CuCl, CuBr or CuCN. The mechanism is a bit more complex and involves radicals.
Mechanism involving a benzyne
Normally, halogenoarenes cannot make usual SN2 or SN1 reactions. However, in very harsh conditions of temperature and of pH, it is possible to force such reactions.
The mechanism involves a triple liaison in the cycle, the species being called a benzyne, The existence of this intermediate has been shown by an isotopic labelling. The C bound to the halogen is an isotope and we observe a racemic melange as product: