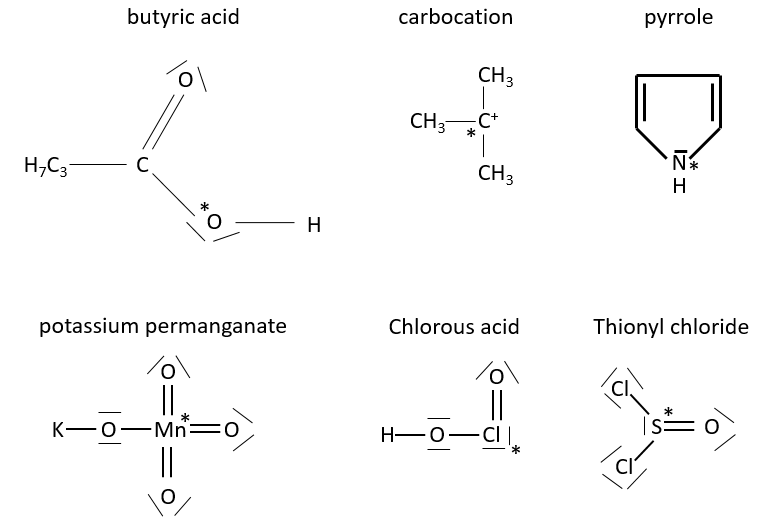
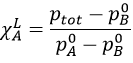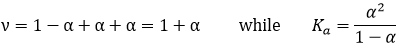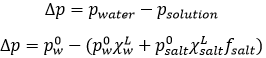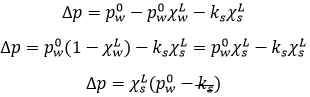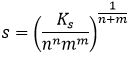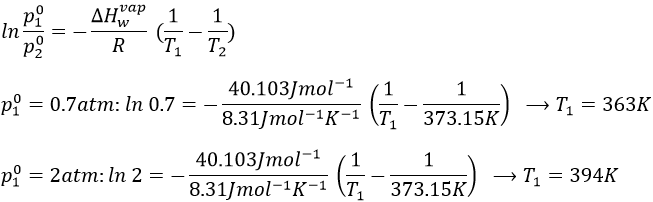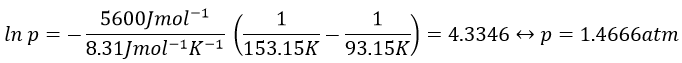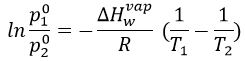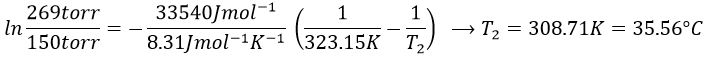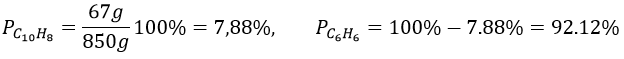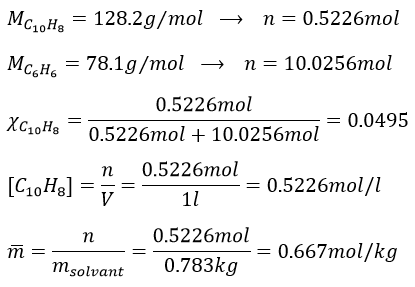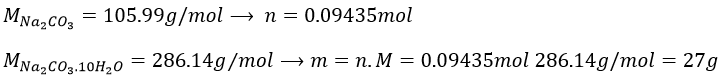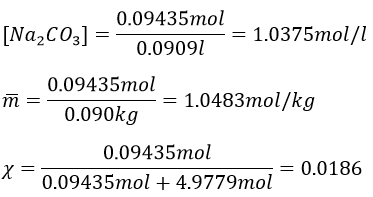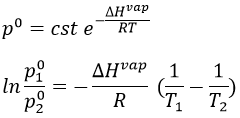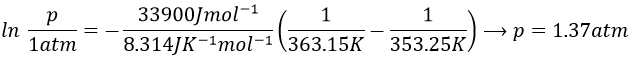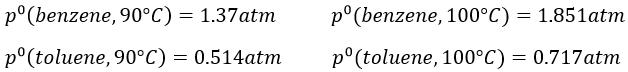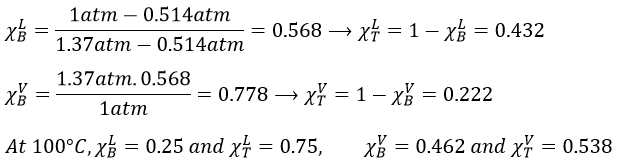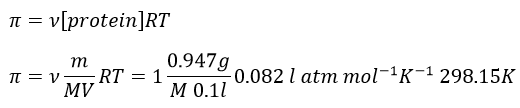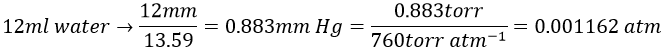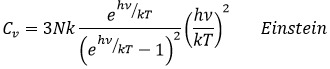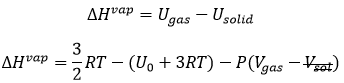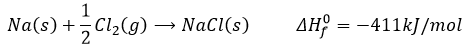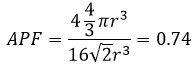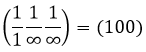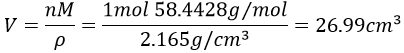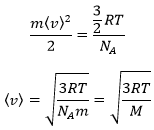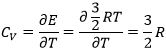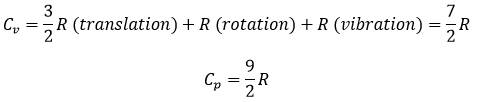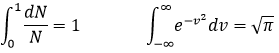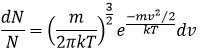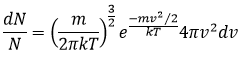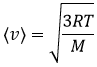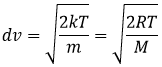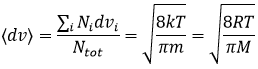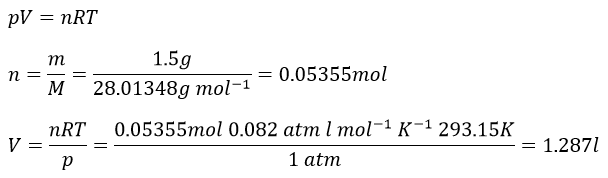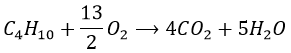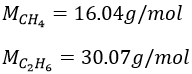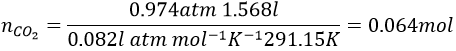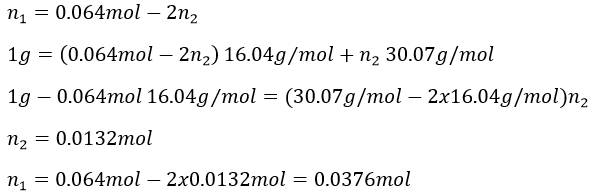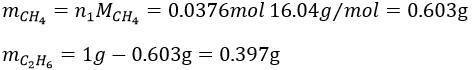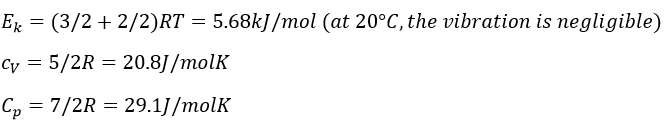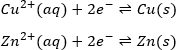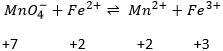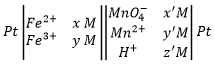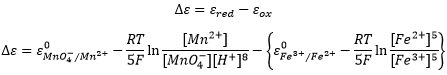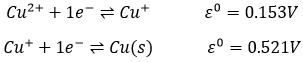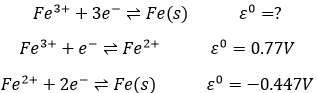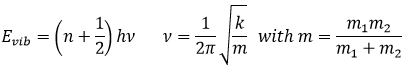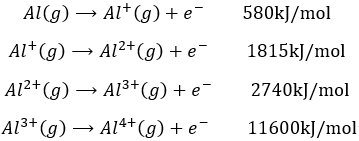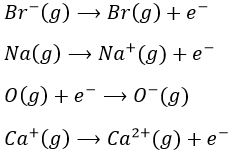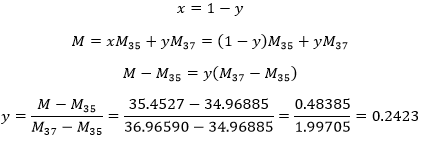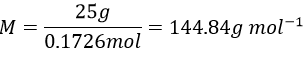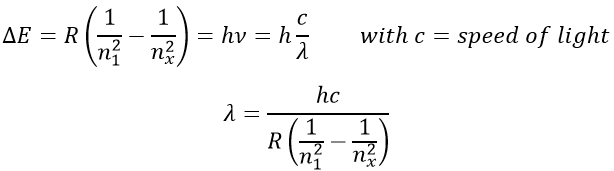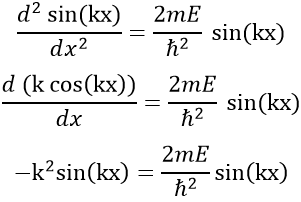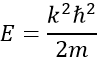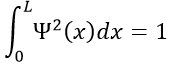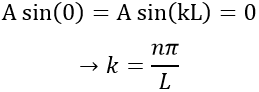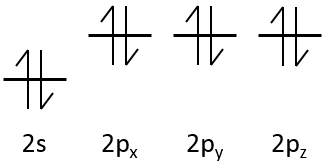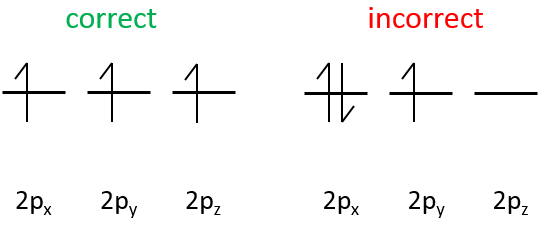Chapter 10 : solids – conductivity
Electric conduction
Some solids are conducting the electricity and some are not. We will explain here from where the conductivity comes and the difference between a conductor and an insulator. The conductivity is explained by the band theory.
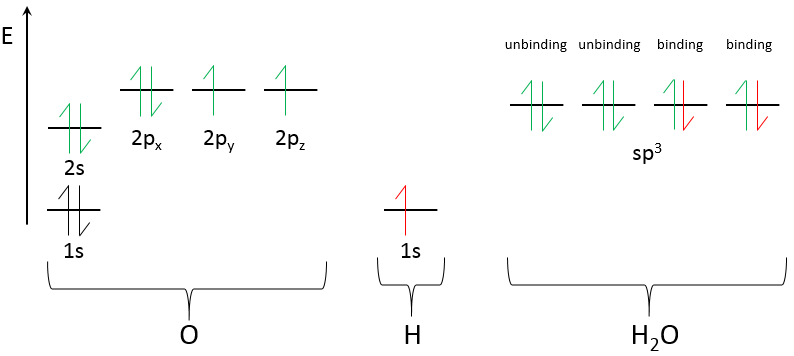
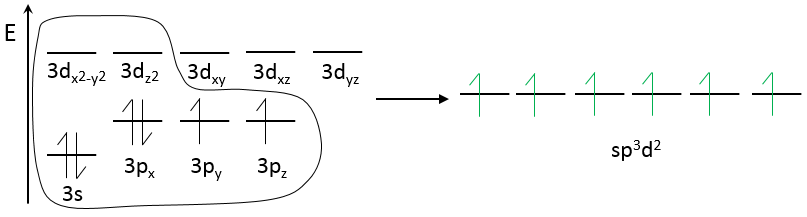
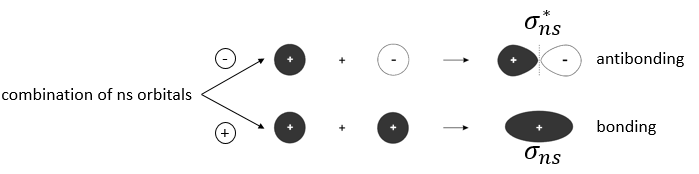
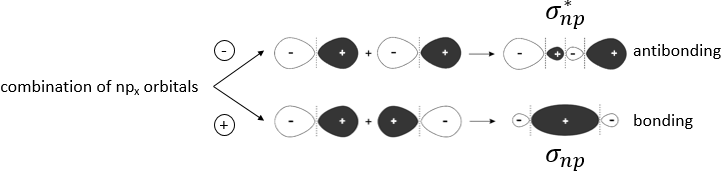
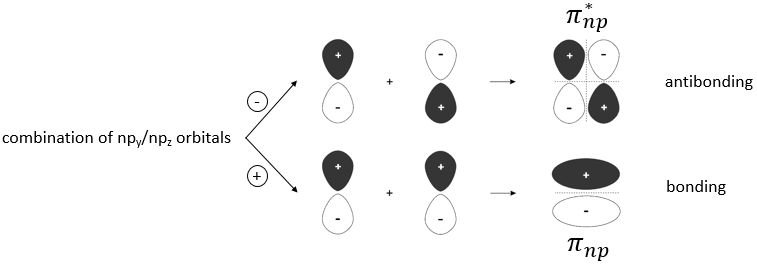
We have seen in the section on molecular orbitals that liaisons are the combination of the atomic orbitals of the bound atoms.
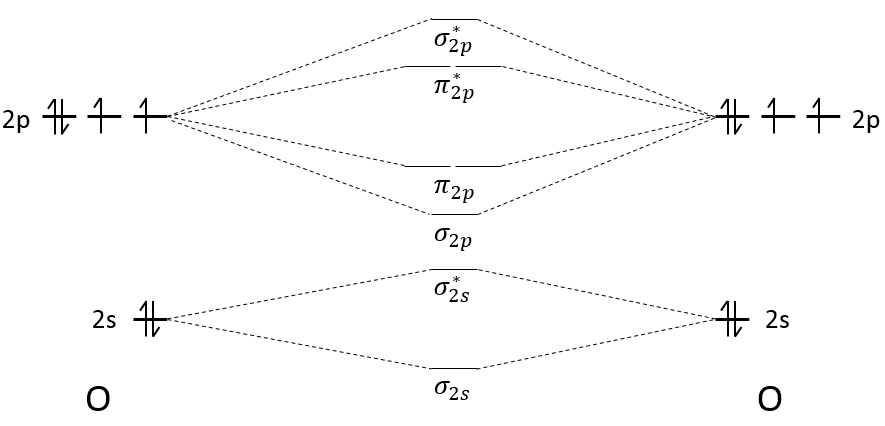
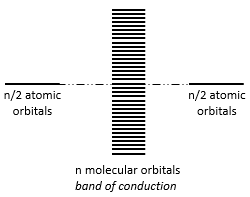
The width of the band increases with the number of atoms but the difference of energy between the molecular orbitals decreases significantly and in metals, the atoms are all bound together, leading to a continuum of molecular orbitals, a band.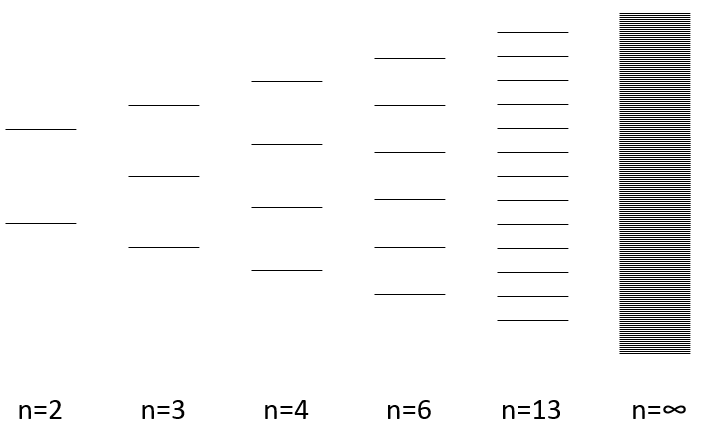
The energy required to an electron to jump from a lower orbital to a higher one is thus small inside the bands and a simple thermic agitation may be enough.
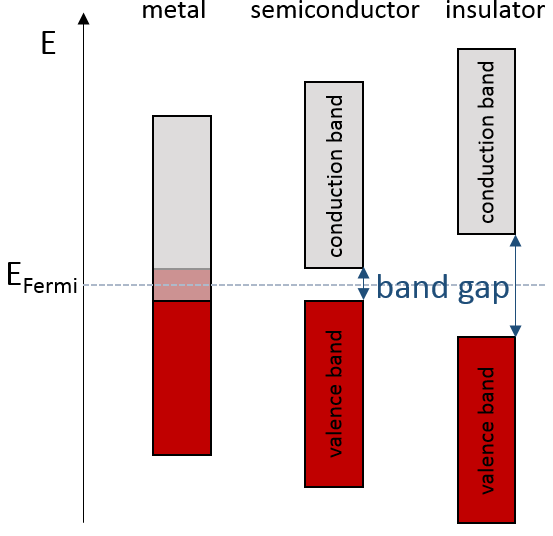
The bands can extend on a wide range of energy but there can be some space between two bands of molecular orbitals. The ranges of energy not covered by any band are called band gaps. In some cases, there is no gap between two bands: the bands overlap.
The electrons in solid respect the Pauli principle of exclusion: lower energy levels are filled first and by pairs of electrons. The highest occupied molecular orbital is called HOMO and the lowest unoccupied molecular orbital is called LUMO. The HOMO and LUMO can be in the same band or in bands separated by a gap.
The Fermi–Dirac distribution f(ϵ) gives the probability that (at thermodynamic equilibrium) an electron occupies a state having an energy ϵ.
T is the temperature, k is the Boltzmann constant and μ is the total chemical potential. The chemical potential is a form of potential energy that can be absorbed or released during a chemical reaction or a phase transition.
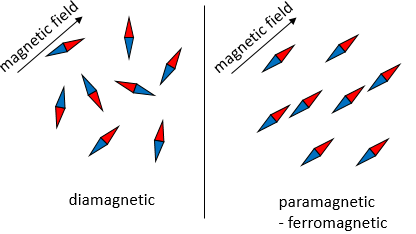
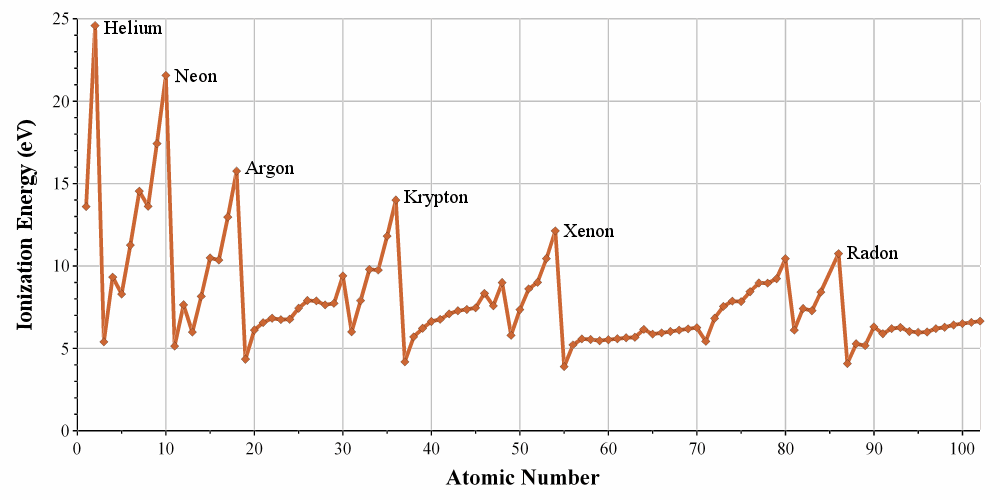
If there is a state at the Fermi level (ϵ = µ), then this state will have a 50% chance of being occupied at any given time. It is in the vicinity of the Fermi level that we find the LUMO and HOMO orbitals. The conductivity of a solid will depend on the ability of electrons to pass from a HOMO to a LUMO orbital. In a metal, the Fermi level is in a band and it is thus very easy for electrons to jump from the HOMO to an unoccupied orbital. Also remember that in metals, some electrons are not bound to atoms but are shared and can move inside the solid. For those reasons, metals conduct well electricity.
The Fermi level in semiconductors is in a small gap. It is then necessary to give an additional energy, equivalent to the energy gap, to the electrons to make them reach the LUMO. The band just beneath the Fermi level is called the valence band because the electrons of valence are in this band at the equilibrium. The band just above the Fermi level is called the conduction band. A semiconductor conducts electricity when electrons can jump from the valence band to the conduction band. In an insulator, the gap is larger and it is thus difficult for electrons to reach the conduction band.
Superconductivity
Considering this, an increase of the temperature leads to a better conductivity. However, it is not always true. Superconductors are particular materials the resistance of which drops to zero when they are cooled below a critical temperature, that can vary depending on the material of the superconductors. It is a quantum mechanical phenomenon characterized by the Meissner effect: when a superconductor is placed in a weak external field and cooled below the critical temperature, the magnetic field can no more penetrate the material (in fact, it does but only on a very small distance). In the superconductors, the electrons are bound by pairs, called the Cooper pairs. Despite the repulsion that we may expect between two electrons, an attraction can exist at very low temperatures due to the electron-phonon interaction. A phonon is a mode of vibration of the atoms of the lattice. The vibration has a given frequency and thus an energy (E=hν). The electrons of a Cooper pair are not necessary close together because this is a long range interaction. This interaction is very small but when we consider many pairs of electrons, the pairing opens a gap in the allowed energy states of the electrons. This gap prevents small excitations of the electrons, what leads to the zero electrical resistance and to the superconductivity.
Superconductors are also the most powerful electromagnets know. Those are used in several applications. One of them is the fastest train on earth, the Maglev, that uses superconductor magnets to levitate several centimetres above the rails.
Thermal conductivity
The thermal conductivity is the quantity of heat that propagates through a material by unit of time. The bigger the thermal conductivity, the better a material conducts heat. An insulation product has a low thermal conductivity. A thermal conductivity of 1 Wm-1K-1 is the quantity of heat that propagates over 1 second through a bloc of material with a surface of 1m2 and a width of 1m when a difference of temperature of 1K is applied between two opposite faces of the material.
The heat propagates from the hottest location towards the coldest location. That may sound obvious, but when we touch something cold, the cold does not comes from the cold object to us, we give heat to the cold object.
When we are cooking, the handle of pans are insulated so that we can grab them without burning our hands. The pan itself has to be a good conductor of heat.
Flaws in crystals
The arrangement in a crystal is rarely perfect. In fact, except at 0K, solids have flaws in their arrangement. It is a result of the second law of thermodynamics (next chapter) that says that the disorder of the universe has to increase during any process. A flaw in a crystal increases the disorder in the crystal: there is only one way to draw one perfect arrangement of atoms but there are many possibilities to place a flaw in this arrangement.
As a result, the single perfect crystal is at the absolute zero. For larger temperatures, the crystal has some energy from the heat that is turned into potential energy through flaws.
Different types of flaws exist:
- Punctual flaw: one individual atom is not placed correctly in the arrangement. Several cases can be sorted:
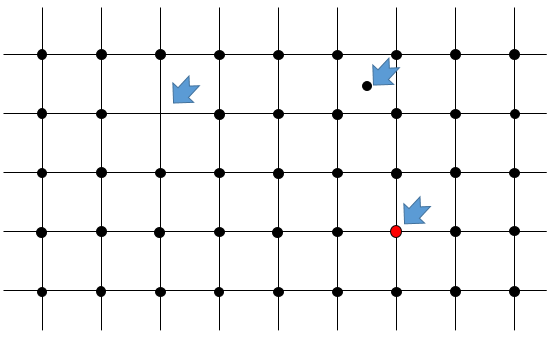
- One atom is missing in the arrangement: it has been expelled from the core of the crystal to its surface. It is called a flaw of Schotty.
- One atom is at the wrong place: the atom is still in the core of the crystal but not aligned with the other atoms. It is called a flaw of Frenkel.
- One atom has been replaced by another one
- Linear flaws: one line of atoms is out of the arrangement.
- Planar flaws: it comes from the merging of two crystals growing in different directions.
Alloys
An alloy is a solid composed of several elements and having the properties of a metal. Different types of alloys exist:
Alloy of substitution: some atoms of the metal are replaced by other atoms of similar size. The stainless steel is an alloy of substitution for which some Fe are replaced by Cr and Ni, respectively in the proportions of 18% and 8%.
Interstitial alloy: Small elements are added in the interstices between the atoms of the network. If you remember, we have seen that there is a lot of empty space in crystals and small ions can be inserted in the holes between the atoms.
Mixt alloy: it is a combination of the interstitial alloy and of the alloy of substitution.
The properties of the alloys depend on the elements composing the alloy and can drastically change from the properties of the main metal. A metal like the aluminium that is flexible can become hard if we mix manganese with it. However, this mix makes the solid very sensible to water.
Doping of semi-conductors
Semi-conductors can be doped by the intentional addition of impurities in their structure. The impurities have the effect of adding or removing electrons from the lattice. In the case of additional electrons, those are destined to fill the band gap between the valence and the conduction bands. Removed electrons come from the valence band so that the gap is displaced.
The semiconductors of the column IVa are doped by elements of the columns IIIa or Va. The replacement of a Si by a P (Va) increases the amount of electrons in the lattice. It is also the case when an element of the column IIIa (as B) is inserted in the holes of the lattice. A doping where electrons are added in the lattice is called of type n (n for negative), or n-type. We also say that Si uses P as a donor (of electron).
Elements of the column IIIa can also replace atoms of Si in the lattice. In this case, the lattice loses one electron by replaced atom. The inserted atom, Al for instance, has an electron less than the other atoms. It creates a “positive hole” in the lattice. A doping where electrons are removed from the lattice is called of type p (p for positive), or p-type. We also say that Si uses Al as a captor (of electron).
The semi-conductors or the other columns can also be doped the same way by elements of a lower or higher column.
Diodes
A p–n junction diode is made of a crystal of semiconductor, Impurities are added to it to create, on one side a region that contains electrons, forming a n-type semiconductor, and on the other side a region that contains holes, forming a p-type semiconductor. The boundary between these two regions, called a p–n junction, is where the action of the diode takes place. When those two materials are attached together, a flow of electrons occurs from n to p side. As the electrons flow there is now a region where no charge carriers (electrons and holes in this case) are present. This region is called the depletion region. The crystal allows electrons to flow from the n-type side (called the cathode) to the p-type side (called the anode), but not in the opposite direction.
Chapter 9 : Phase diagram
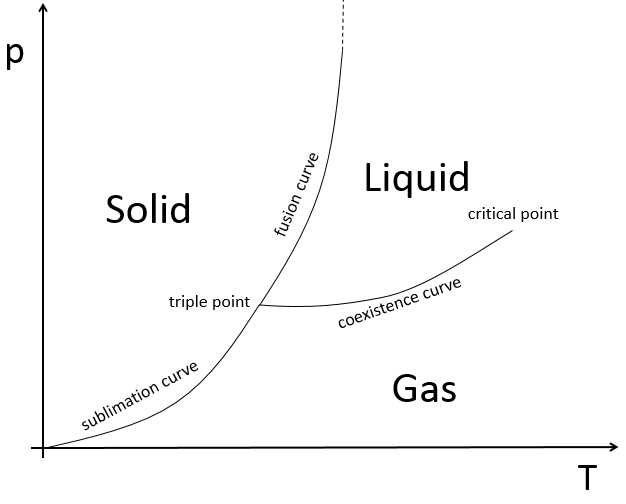
The state of compounds depends on the temperature and on the pressure. We map the states of the matter on the diagram of phases. The pressure is put as ordinate and the temperature as abscise.
The states are separated by full lines, the curves of transition of phase.
The curve between the liquid and the solid is called the curve of fusion.
The curve between the liquid and the gas is called the curve of vaporisation/coexistence.
The curve between the solid and the gas is called the curve of sublimation.
Curve of vaporisation
In a closed system containing a liquid and a gas, there is an equilibrium between the two phases. The gas becomes liquid at a given speed vGL and the liquid becomes gas at a given speed vLG. The equilibrium is reached when those speeds are equal.
The liquid becomes a gas if the molecules have a kinetic energy large enough. If this energy is not large enough, the molecules remain liquid because the interactions between the molecules make it more favourable. The kinetic energy can be provided by heating or excitation. Typically, we have to heat water to make it boil.
The other reaction, from a gas to a liquid is favourable but is not complete because of the entropy. The entropy is an expression of the disorder in the system. The second law of thermodynamics (the thermodynamics will be explained in its own chapter) imposes that the universe evolves towards a greater disorder. It means that the sum of the variations of entropy inside and outside the system has to be positive.
There is thus a competition between the increase of entropy and the decrease of the energy in the system.
The free enthalpy of Gibbs represents/reflects this competition:
The Gibbs free enthalpy is thus a thermodynamic potential taking into account the implications of the system on its environment.
The vapour pressure in the system at the equilibrium p° (also called the pressure of Clausius-Clapeyron) is
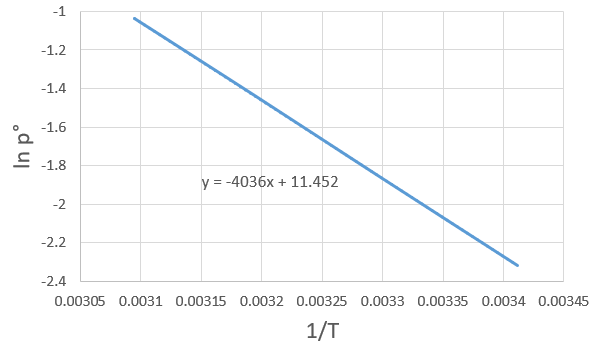
The entropic terms are present in the pre-exponential constant and the enthalpy is in the exponential term. As the temperature increases, the vapour pressure increases exponentially. Experimentally, we can find the enthalpy of vaporisation by plotting the curve ln p° vs 1/T.
The slope of the curve is –ΔH/R. The value of ΔHvap depends on the interactions between the molecules. Strong interactions mean that the molecules are not easily getting away from each other and that the vaporisation requires more energy, i.e. ΔHvap is large and p° is small. It is logical: if the molecules don’t easily vaporise, there are not a lot of molecules in the gas and the pressure of the vapour is thus low.
In the cyclohexane, there are barely no interactions between the molecules and its ΔHvap is small. The cyclohexane is a volatile liquid.
The boiling temperature of a liquid is the temperature at which the vapour pressure of a liquid is equal to the atmospheric pressure. For the water, this temperature is 373K (100°C) if the atmospheric pressure is 1 atm. In altitude, the atmospheric pressure decreases and so does the boiling temperature. For example, the boiling temperature is 363K (90°C) at an altitude of 3000m. In a pressure cooker, the pressure is greater than 1 atm and the water boils at a temperature larger than 100°C.
Curve of sublimation
The sublimation is the transition of phase between a solid and a gas
We can define a vapour pressure for solids too, but it is much lower than for a liquid because interactions in a solid are stronger than in a liquid. The equation is similar
But the constant is different and ΔHsub>>ΔHvap, for the exact same reasons.
Curve of fusion
The fusion is the transition of state from a solid to a liquid.
We can also define a pressure such as
The enthalpy of fusion is very small and the curve is almost a right vertical line. In general, the slope is positive, meaning that when a liquid becomes solid (by decreasing its temperature for example), its volume decreases. It is however not always true.
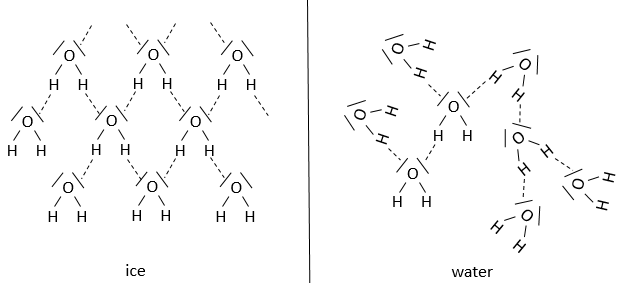
A particular case is the water: the volume of 1kg of water is smaller than the volume of 1kg of ice. It is a tip of the barmen to decrease the volume of drink that they give to their clients but it is also what allow us to ice-skate:
When we skate, all our weight is applied on a very small surface. The ice at this place instantly becomes liquid because of this pressure. If the ice did not change into liquid, the friction between our skates and the ice would be much larger, as it is in general the case between two solids. The small puddle of water that is formed lubricates the ice and allow us to slide with almost no friction. Because the volume of water was smaller than the volume of ice, the water remains in the small hole that our skates dug in the ice. After our passage, the water turns back into ice at the same place where we skated. If the volume was the water was larger than the one of the ice, the puddle would extend near the skates and deform the surface of the ice. If it was the case, in a skating rink, the surface of the ice would not remain flat for a very long time.
The carbon dioxide in an extinguisher is in a liquid state, near the triple point. When we use the extinguisher, the pressure drops suddenly. We should thus expect a gas outside of the tube. However, there is a detente of the gas during the process (moving from a narrow space to a large space) that involves a decrease of the temperature, making the gas become a solid.
Variance
It is the number of degrees of freedom that characterise a state
Where c is the number of constituents of the matter and φ is the number of phases. Let’s take a look at different points on the phase diagram
- in the middle of a phase: V=1-1+2=2: we can modify the pressure or the temperature without transition of state.
- on a curve: V=1-2+2=1: if we want to modify the pressure or the temperature of the matter without transition of state, the other parameter (T or p) has to be fixed.
- on the triple point: V=1-3+2=0: if we want to keep the matter in this state, we can’t change the conditions of temperature and of pressure.
At the triple point, the enthalpy of sublimation equals the sum of the enthalpies of vaporisation and of fusion. The triple point for the water is at t=273,16K and p=0.006atm.
Another remarkable point is the critical point:
After this point, the liquid and gaseous phases become indistinguishable. In water, the critical point occurs at around 647 K and 218 atm.
In the vicinity of the critical point, the physical properties of the liquid and the vapour change dramatically, with both phases becoming ever more similar. For instance, liquid water under normal conditions is nearly incompressible, has a low thermal expansion coefficient, has a high dielectric constant, and is an excellent solvent for electrolytes. Near the critical point, water becomes compressible, expandable, a poor dielectric, a bad solvent for electrolytes, and prefers to mix with nonpolar gases and organic molecules.
At the critical point, only one phase exists. The heat of vaporization is zero.
Above the critical point (T>Tc and p>pc) there is a state of matter that is continuously connected, without transition of phase, with both the liquid and the gaseous state: supercritical fluid. Such a fluid has usually properties between those of a gas and a liquid.
Case of mixtures
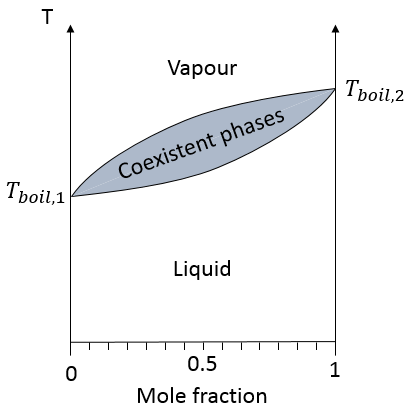
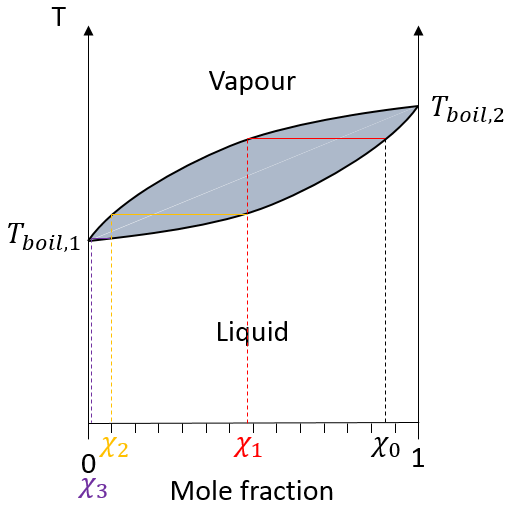
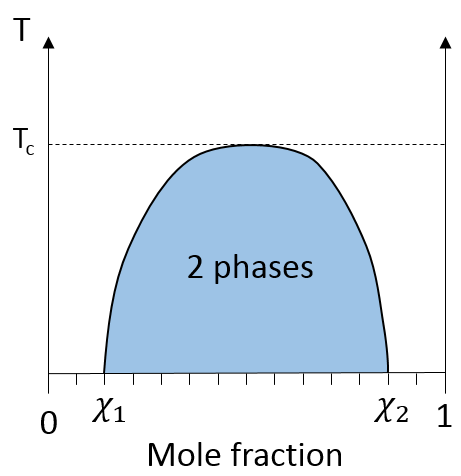
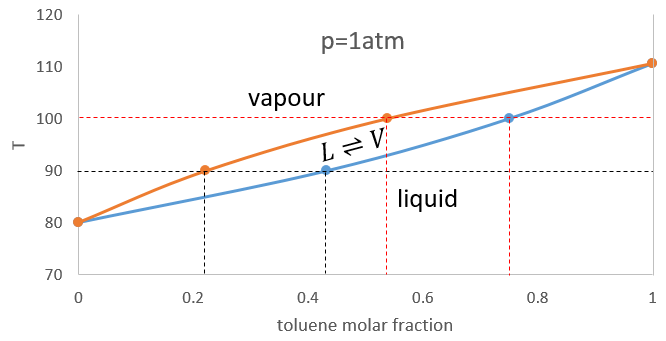
In a solution, the elements of the mixture don’t necessarily have the same boiling point. The element of lower boiling point will evaporate faster than the other components of the mixture. If we consider a binary mixture, we can plot the composition of the melange in function of the temperature on a diagram shown underneath
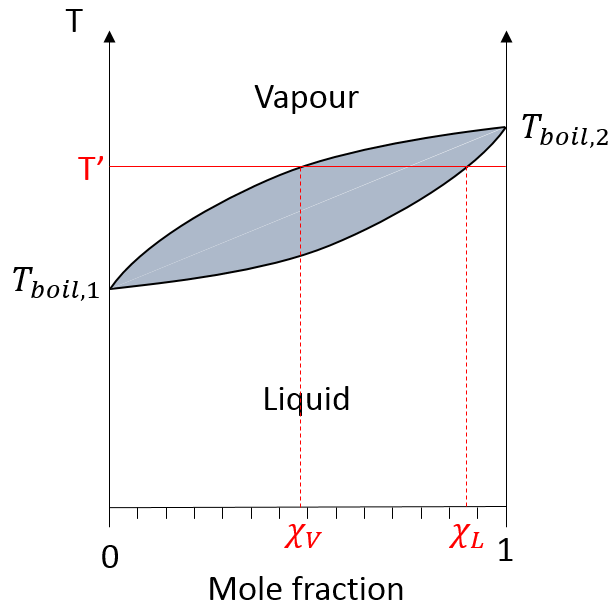
On this diagram, the temperature is reported on the ordinate and the mole fraction χ of the second component of the melange is set as abscise. At χ=0, the solution is a pure solution of the solute 1, and the boiling temperature of the solution is Tboil,1. At χ=1, the solution is a pure solution of the solute 2, and the boiling temperature of the solution is Tboil,2. In between, the solution is a mixture of the two components. In this case, we considered a solution in which the solute 1 has a lower boiling temperature than the solute 2. If we increase the proportion of the solute 2, the boiling temperature of the mixture increases. This increase is not linear and one can see that there is an area in which both vapour and liquid coexist. If you look at a given temperature T’, the composition of the liquid and of the vapour is different: the composition of the vapour is composed by a larger fraction of the most volatile solute than the liquid.
The molar fractions of the melange can be determined with the law of Raoul. The total pressure of an ideal mix is the sum of the partial pressures of the gases
The partials pressures are proportional to the mole fraction of the compound in the solution χLA multiplied by the vapour pressure of the pure compound p°A:
The total pressure is thus
Given that the sum of the mole fractions in solution is equal to 1, i.e. χLA+ χLA=1, we find the mole fraction of one species from the pressures
Moreover, this allows us to connect the vapour and liquid mole fractions together by
Distillation
The distillation is a separation process based on the difference of boiling temperature of different solutes in a solution. Basically, if the initial solution has a mole fraction χL, we can boil it at the temperature T’. The goal is to collect the vapour and to liquefy it. The collected solution has a composition χV. We can keep doing this multiple times to obtain a virtually pure solution of the solute 1.
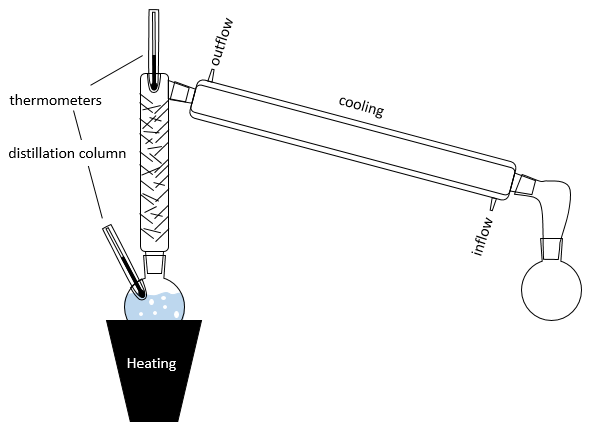
In practical, multiple distillations are done at once. The setup is composed by a balloon containing the initial solution, a heating system (as an infra-red lamp), a column of distillation, a cooling tube and a balloon to collect the distillate. Thermometers can be placed in the first balloon and at the top of the distillation column to control the temperature of the solution and of the vapour.
The cooling device is composed of two tubes, one thinner placed inside the other one. The inner tube has openings at both extremities and is connected to the column and the collecting balloon. The other tube has lateral openings connected to a counter flow of cool water. The flow of cool water goes this way to avoid an unfilled area and also because the water near the column, that has been heated by the vapour, is quickly evacuated. If the water was going in the opposite direction, the water gets heated by the vapour and the cooling power of the tube would be decreased.
The distillation column if filled with small pieces/tubes of glass to increase to surface of contact with the vapour. In some columns, needles are part of the column and no additional pieces have to be added.
In the distillation column, hot vapour goes up and meets the pieces of glass of lower temperature. At their contact, there is an exchange of heat and the vapour may turn back into liquid, not with the composition of the liquid in the balloon χ0 (to keep the notation of the figure above), but the composition of the vapour χ1. Droplets will eventually fall back into the balloon or evaporate on their way because of the hot vapour. Their composition will now be χ2, as if two distillations had been performed. The vapour continues its way up to the top of the column, getting more pure, and enters the cooling tube where it turns into liquid, finishing its path inside the collecting balloon.
It is good to put some pumice stones in the balloon to avoid overheating and to obtain bubbles of a controled size.
Azeotropes
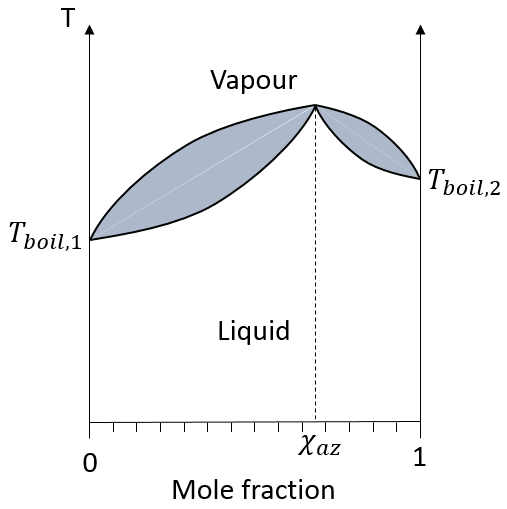
The diagram of boiling is not always that simple. Some mixtures are said to be azeotrope. An azeotrope mixture acts like a one-component solution, i.e. the mole fraction does not change during the boiling. On the diagram, the curves look like
If the initial solution has the azeotrope composition, the liquid and vapour compositions are identical and do not change over time. If the initial solution has a smaller mole fraction, we will eventually obtain a pure solution of the solute 1 but it is impossible to obtain a pure solution of the solute 2: the composition tends towards the azeotrope. The same is true if the initial composition of the mixture has a larger mole fraction than χaz: it will be impossible to obtain a pure solution of the solute 1 in this case.
Two types of azeotropes can be sorted: the positive ones and the negative ones. The differences is simply their boiling temperature. On the diagram above, a positive azeotrope is represented: its boiling temperature is larger than the ones of the pure components of the mixture. A negative azeotrope has a lower boiling temperature.
Demixing
In mixtures, different interactions exist: the interactions between two identical molecules and between the different molecules of the mixture. If
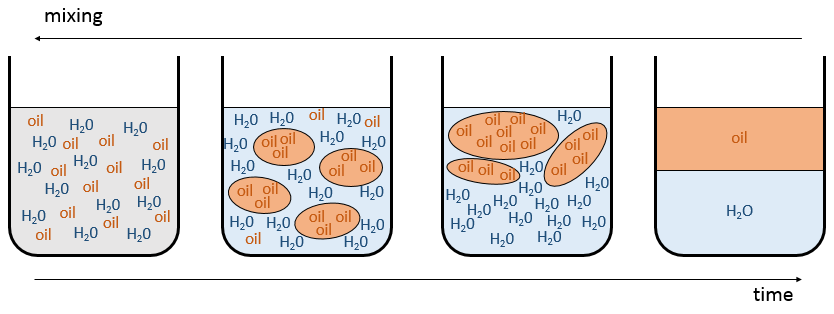
then the mixture tends to separate. The expression above means that the interactions between identical molecules are more favourable than the interactions between different molecules. Imagine that in that case the molecules A and B are perfectly mixed together. The interactions between A and B are not necessarily unfavourable but with the Brownian motion, the molecules will tend to regroup between species and they will form clusters/bubbles to have the maximum amount of favourable interactions. That is how emulsions form. The clusters will merge together over time to improve the ratio volume/surface of the clusters and the solution will eventually end as two separated phases. It is the phenomenon of demixing.
For example, oil and water do not mix well. They form two separate phases. Yet, we can dilute a bit of water in oil or vice versa but if we continue to add water, the phases will separate. It is shown on the following figure.
If the oil is the component 1 and water the component 2, this figure shows that we can add water to oil up to the mole fraction χ1 before a separation of phases. We can add oil into water without demixing for mole fractions larger than χ2. As we can see, the demixing process depends on the temperature. The quantity of solute that we can dissolve before the demixing depends on the local temperature. Above a critical temperature (not the same as in the phase diagram), the mixture will remain as one phase no matter the composition.
Colligative properties
The colligative properties are properties that depend on the number of the particles in the solvent, of the solvent but not of the solute species. The fact that the boiling temperature of water increases when we add a bit of salt inside is a colligative property. It does not matter that it is salt or something else. The temperature of freezing decreases as well: we use salt on snow to make it melt. In the phase diagram, the coexistence curve has been translated down because of the addition of the salt. The ebullioscopic law says that
With kb the ebullioscopic constant and ms the molality of the solute. When we add salt into water, we add two species: the ions Cl– and Na+. It is thus better to write this relation as
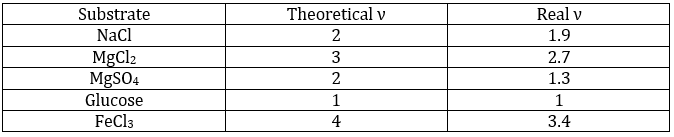
ν is called the van’t Hoff factor and is the number of ions found by unit formula. In fact, we observe that this factor is often smaller than its expected value: some of the molecules don’t dissolve in the solution.
That means that for 100 molecules of NaCl in solution, 90 will dissolve to produce the ions Cl– and Na+ and 10 molecules don’t dissolve (making a total of 190 molecules instead of 200). ν can be determined from the constant of dissociation of the molecule. For example, all the molecules of a weak acid don’t dissociate in water.
The Ka of this reaction is
Let’s take a look at the concentration of the species before and after the reaction. In fact, instead of the concentrations, we will consider the concentrations/initial concentration of CH3COOH.
The total number of molecules is
So, we know that there is a decrease of temperature due to the colligative properties. The variation of temperature is coupled to a variation of the vapour pressure of the mixture. Intuitively, the vapour pressure of the dissolved salt is in general very small with regards to the vapour pressure of the water. Some salts are not volatile at all. The pressure is equal to the sum of the partial pressures
The addition of a salt B into the solution A has thus lowered the pressure.
The mathematical demonstration follows:
Considering the dissolution of NaCl in water, the variation of pressure is
Fsalt is a coefficient of activity of the salt, present for reasons similar to that of the van’t Hoff factor ν.
We can still simplify the expression:
On the phase diagram, the coexistence line is translated downwards by Δp. The ΔT can also be calculated:
The derivative gives
Math tells us that it also gives
So
dp°/dT is in fact equivalent to Δp/ΔT from the phase diagram. We obtain that
The difference of temperature is thus proportional to the square of the temperature and directly proportional to the amount of species in the solvent.
Similarly, it is possible to detect if solids are pure. If a solid melts at a temperature lower than its normal melting temperature, it shows that there are impurities in the solid.
The osmotic pressure is also a colligative property: in cells, the concentration of ions must be identical at each side of the cell membrane. Otherwise the cell expends or shrinks. The osmotic pressure of a solution is the difference in pressure between a solution containing solute particles and the pure liquid solvent when the two are in equilibrium across a semipermeable membrane, i.e. a membrane which allows the passage of solvent molecules but not of solute particles. If the two phases are at the same initial pressure, there is a net transfer of solvent across the membrane into the solution known as osmosis. The process stops and equilibrium is attained when the pressure difference equals the osmotic pressure.
Solubility
The solubility is the ability of a substrate to dissolve in a liquid. We are talking of solubility for solids, salts for instance, and for gases.
Solubility of gases
Some unnaturally sparkling mineral water sold in the market are enriched in carbonic gas. A given quantity of gas can be dissolved in a liquid by the direct injection of the gas into the liquid with a given flow. This quantity is not infinite and depends on the conditions of pressure and of temperature. If a large pressure is applied, more gas can dissolve in the liquid. The quantity is proportional to the vapour pressure p° of the gas.
fA is a function that depends on the molecule. The molar fraction of A in the solution is thus proportional to the pressure of the gas multiplied by a constant kA=p°A fA. We can rewrite this in function of the concentration in the solution instead of the molar fraction as
A way to dissolve a gas inside a liquid is thus to increase the pressure of the gas.
Acidification of the oceans
We often hear about the greenhouse effect and about the massive impact that the modification of the concentrations of the greenhouse gases may have on our lives. An important actor of the greenhouse effect is the CO2. Animals exhale CO2 and ours industries and locomotion middles (cars, trains, planes, etc) also produce a lot of this gas. Plants are consuming the CO2 to produce O2 that we breathe. It is a fragile equilibrium that we are menacing with the deforestation, but it is not our point here. The point is that oceans represent a colossal volume of water in which CO2 may be absorbed (each day, it absorbs 4kg of CO2/man, 25 billion kg CO2/year). In the oceans, algae’s are playing the same role than the plants on the ground and their effect is probably as important with regard to the quantities of CO2 absorbed. A global increase of the concentration of CO2 would increase the quantity of CO2 in the oceans, forming carbonic acid (H2CO3) that acidifies the water, slowly menacing the lives of oceanic species, including algae’s, planktons, corals, etc. Before the industrial revolution, the pH of oceans was 8.2. The actual pH is 8.05 and is expected to decrease to 7.8 at the end of this century.
Another way is to change the temperature. At the beginning of this chapter, we discussed about the free enthalpy of Gibbs G=H-TS. The temperature is thus coupled with the entropy. The ΔG associated with the transition of phase is thus directly dependant on the temperature multiplied by the variation of entropy due to the transition of phase. The dissolution of a gas in a liquid decreases the entropy of the system: the disorder is greater in a gas where there is a lot of space to move and barely no interactions between the molecules than in a liquid where the space is limited and interactions may be strong. On the other hand, the dissolution is exothermic: new liaisons are generated. As a result, there is a competition between the entropy and the enthalpy of the dissolution. The enthalpy can be expressed by ΔH=-RTlnχL2, from the van’t Hoff equation ln Csat = -DH/(RT) + Const.
We can visualise the dissolution of a gas in a liquid with this diagram:
The energy is put as ordinate and the mole fraction of the gas in the liquid is put as abscise. A horizontal dashed line is traced at E=ΔH° and two dotted lines at E=TΔS, T1<T2. We will call those lines the enthalpic and the entropic lines. Those lines are in the negative values of the energy as explained before. Next, we trace the curve ΔG(χL2)=TΔS- RTln χL2. This curve has been plotted for two temperatures. The curves terminate for χL2=1 at E=TΔS, i.e. it crosses the entropic line. On its path, the curve crosses the enthalpic line. At the crossing point, we find the maximum amount of gas χ1 that the liquid can dissolve. For larger temperatures (red lines), the entropic line moves deeper in the negative values of E. The curve of ΔG translates the same way, still ending at E=TΔS. ΔH doesn’t change. The crossing point between ΔG and ΔH indicates now a smaller mole fraction of gas χ2 into the liquid. An increase of temperature involves thus a decrease of the solubility of the gas. As a reminder from the phase diagram and the curve of coexistence, the heating of a liquid increases the kinetic energy of the molecules and molecules with a kinetic energy large enough become gaseous.
Solubility of solids
Salts dissolve into ions in polar liquids such as water.
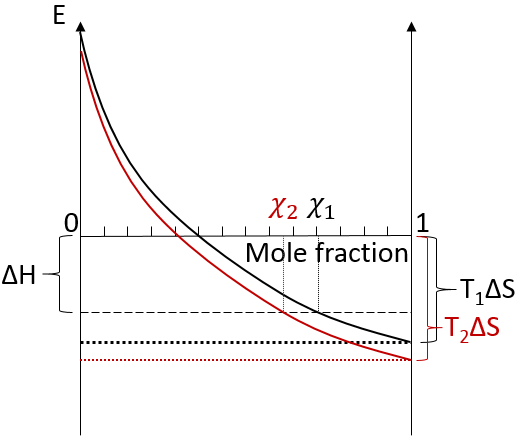
In opposition to the solubility of gases, when solids dissolve in water, the entropy increases slightly: first, solutions are ordered (short range order) but solids are more ordered than them. This variation of entropy is small with regards to the variation of entropy of the dissolution of gases. Second, there are more molecules as one molecule of salt gives several ions. Also, the dissolution is endothermic: liaisons are broken to form the ions. Both ΔH and TΔS are thus positive. We determine the quantity of salt that can be dissolved the same way as for the gases. Now that the enthalpic and the entropic lines are in the positive energies, if the temperature increases, the solubility increases.
Some salts have a negative enthalpy. In this case, the enthalpic line is under the entropic lines whatever the temperature.
There is thus no crossing point between the curve of ΔG and ΔH. The salt is said to be infinitely soluble in this case.
Constant of solubility Ks
The dissolution of a solid inside a solution respects the rules of a chemical reaction: the stoichiometry is respected and the reaction has a constant of reaction defining the speed at which the process takes place. Let’s define s as the maximum concentration of the salt that can be dissolved. If we put more solid in the solution, crystals will remain (in general) in the bottom of the solution.
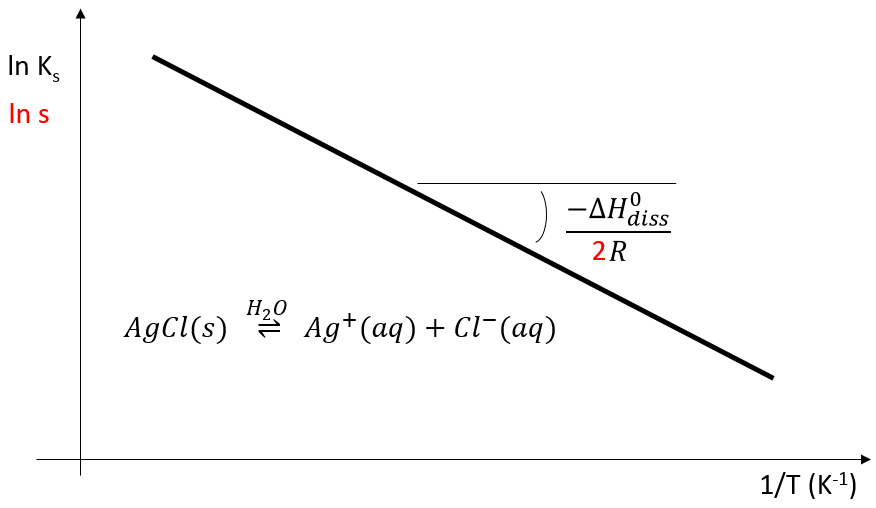
In this situation, the concentration of the ions in solution can directly be related to s. For instance, the dissolution of AgCl into water leads to the following equation
With the constant of solubility Ks
As the solid is pure, its concentration is considered as equal to 1 in the equation. It is the case for any solid. When no more salt can be dissociated, the concentration of both ions Ag+ and Cl– are equal to s.
s is thus equal to √Ks. For CaF2, three ions are formed during the process.
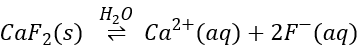
The constant of solubility Ks is
In this second case, there are two anions F– in solution for each dissolved CaF2. Its concentration won’t be s but 2s.
As a general expression,
With m and n the charge of the ions, or their stoichiometric coefficients (it is equivalent).
The value of Ks gives us precious information on the solubility of a salt, and on how much solid we can put in solution without waste. Remember that Ks depends on the temperature and that it is sometimes necessary to heat a solution to dissolve a precipitate, to reach a given concentration of ions.
This relation is very similar to the expression (Clausius-Clapeyron) for the vapour pressure in the system at the equilibrium p° which was seen at the beginning of this chapter
It is thus again possible to plot the evolution of Ks or of s with regard to the temperature
The 2 under the fraction bar is the exponent of s in the relation between Ks and s.
Exercises
1. What is the temperature of ebullition of water at 0.7atm? At 2 atm? (ΔHwvap=40kJ/mol)
2. Determine the vapour pressure of nitrogen at T=-120°C knowing that its usual ebullition point is -196°C and that ΔHvap=5.6kJ/mol.
3.
The following table shows some experimental measurements of the vapour pressure of the benzene as a function of the temperature.
Determine the enthalpy of vaporisation of the benzene. If a sample of benzene at T=50°C and p=150mm Hg is cooled down to 40°C in a closed recipient, will it condense? At 30°C? Estimate the temperature at which the gas stats to condensate.
4. In one mole of ice, there are two moles of H bonds. Determine the energy of the H bonds in one mole of ice if you know that at the triple point the enthalpies of fusion and vaporisation are respectively 333.9J/g and 2493.7J/g. Can you estimate the amount of H bonds in the water?
5. In the following systems, how many phases, independent components and variance?
- water in equilibrium with its vapour at 1 atm
- water in equilibrium with its vapour
6. 1l of naphthalene C10H8 in benzene C6H6 has 67g of solute in it. Give the mass fraction, molar fraction, molarity and the molality in naphthalene if the density of the solution is equal to 0.850.
7. Which mass of decahydrated carbonate of sodium do you have to weight to prepare 100g of a solution of Na2CO3 10%, knowing that the density of the solution will be 1.10. Determine the molarity, molality and molar fraction in Na2CO3.
8. We mix together 30ml of n-heptane (ρ=0.684) and 20ml of n-octane (ρ =0.703). Their vapour tensions at 100°C are respectively 829 and 344torr. Find out the molar fraction of the solution and of the vapour if the temperature is 100°C, Is this an ideal solution? Draw the corresponding isotherm (T=100°C) diagram of phases of this melange.
9. The temperature of ebullition of the benzene and of the toluene are respectively 80.1°C and 110.6°C. Their enthalpies of vaporisation are 33.9kJ/mol and 37.4kJ/mol. Determine the vapour pressure of those two compounds at 90°C and 100°C.
Determine the composition of the solution of benzene and toluene that starts to boil at those temperatures if the pressure is 1 atm.
What is the composition of the vapour at those temperatures?
10. How much ethylene glycol (CH2OH)2 has to be dissolved in 2l of water to prevent it to freeze at -10°C considering a constant of freezing Kf=1.86K kg mol-1 for the water)? Same question with CaCl2 instead of the ethylene glycol, considering a total dissociation of the salt.
11. The osmotic pressure of 100ml of a solution containing 0.947g of a protein corresponds to a column of water of 12mm at 25°C. What is the molar mass of the protein?
Answers
1.
2.
3. If we plot ln p0 as a function of 1/T, the slope α equals –ΔHvap/R, so ΔHvap=- αR
The sample is not at the equilibrium but we have the values of the vapour pressure at the equilibrium. At 40°C, the vapour pressure is larger than the pressure in the flask, so the gas doesn’t condense. At 30°C however, the vapour pressure from the table is smaller than the pressure in the flask and the gas condense under the effect of the cold.
To estimate the temperature at which the gas starts to condensate, we chose one value of the table and apply the formula
to determine the temperature at which the condensation begins:
4. At the triple point, the chemical potential are equals. It means that
This enthalpy is the energy required to break the bonds between the molecules, i.e. the hydrogen bonds. As there are two H bonds per mol, the energy of one mol of H bond is 25,57kJ.
We can estimate the amount of H bonds in the water from the enthalpy of fusion. During the fusion, a given amount of H bonds are broken to make the solid ice become liquid.
We know that 25.57kJ are required to break 1 mol of H bond, so we can estimate that 6.01/25.57=0.235 mol are broken during the fusion. There are thus 1.765 mol of H bond/mol of water.
5. The expression for the variance is V=2+c-φ-n where c is the amount of constituents, φ is the amount of phases and n is the amount of fixed parameters.
- V=2+1-2-1=0
- V=2+1-2-0=1
6. The density is the mass by unit of volume, so the litre of solution weights 850g. We have 67g of naphthalene and 783g of benzene. The mass fractions are thus
Knowing the masses, we can find the quantity of moles for both species
7. As the mass of the solution is 100g, we want to have 10g of Na2CO3. To determine the mass of decahydrated carbonate, we first need to know the amount of moles of Na2CO3 in solution.
The volume of solution is 100g/1.1g ml-1=90.90..90..ml
In the vapour, the molar fractions are
This melange is an ideal solution because the n-heptane and the n-octane are both nonpolar species without dipolar moment and unable to form H bonds. As a result, they don’t have any specific interactions together.
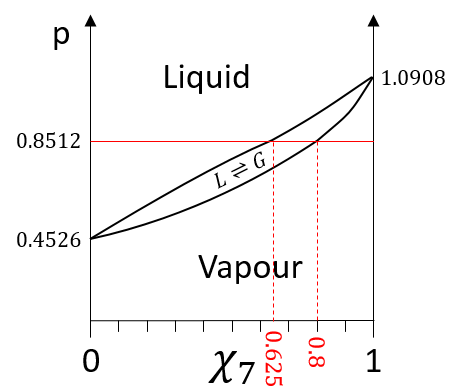
The information we have to draw the phases diagram are that the pure solutions have a vapour tension of 0.4526atm (χ7=0) and 1.0908atm (χ7=1). We also know that at p=0.8512atm, the molar fraction is 0.625 for the liquid and 0.8 for the gas.
8. The partial pressures can be found with the equations of Clausus-Clapeyron
Either we find the constant in the first one with the values we know from the wording to be able to solve the equations at the given temperatures. Or we can use the second equation that doesn’t need to determine the value of the constant.
First method:
Second method:
We do the same for the tow compounds and the two temperatures to find
To determine the molar fractions at a given temperature, we use this expression
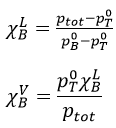
At 90°C, we have
We can plot all those points on the phase diagram.
9.
10.
The osmotic pressure is normally given as a pressure. To obtain it in atm, we transform the height of water in height of mercury and then in atm. The ratio between the density of mercury and water is 13.59
We can now determine the molar mass of the protein
Chapter 8 : Solids – lattice energy
In gases, the heat capacity was a resultant of translation, vibration and rotation.
In a solid, there is no translation and no rotation. The atoms may vibe around their equilibrium position. The vibration involves a potential energy and a kinetic energy, each term participating for ½R. As a solid has 3 dimensions, Cv=3R
However, this equality is not true at low temperatures. It is related to the radiation of the black body. In this case, the heat capacity is given by
A black body is an idealised body that absorbs all electromagnetic radiation (of any frequency). It only emits a radiation called black-body radiation that depends on the temperature alone. A model for the black body is a cavity with a tiny opening.
The radiation penetrating in the cavity are trapped inside because of tis geometry and/or the absorption of the radiation by the walls of the cavity.
At a fixed temperature and considering the thermal equilibrium, the hole may allow some radiation to escape from the black body. It is the black-body radiation and it only depends on the temperature. Because of the size of the hole with regard to the body, the escaping radiation has negligible effect upon the equilibrium of the radiation inside the cavity.
The reticular energy U0, or energy of network is the energy of the solid at T=0K. The energy of the solid at a given temperature is
We cannot measure U0 but we can approximate its value from the enthalpy of sublimation: to determine the energy of the solid, we break all the liaisons to obtain the gas.
The last term comes from the dilatation of the solid into the gas. The volume of the solid is negligible with regard to the volume of the gas. If we consider a perfect gas, then pV=RT. As a result,
We can also find the reticular energy with the Born-Haber cycle explained in a previous section.
For a solid with several elements, such as an ionic solid, the calculation is more complex: there are two or more gases and electronic interactions (ionic liaisons, repulsion).
Born–Haber cycle
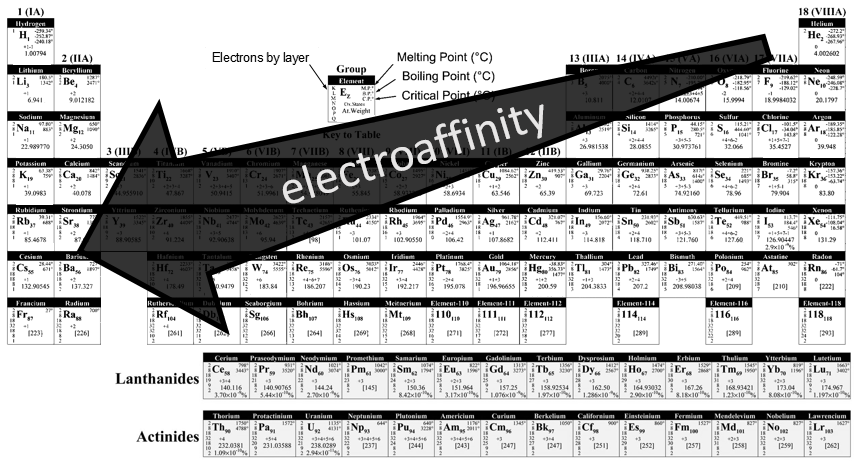
Atoms form solids because it leads to a decrease of their energy. One measure to quantify this stabilisation is the lattice energy ΔH0L, i.e. the energy required to form a solid from the gaseous ions.
This energy is negative and cannot be determined experimentally. The usual way to determine it is to build the so-called Born–Haber cycle. This cycle is made from the basic transformations of the constituents, taken them apart one from each other and starting from their normal state at sctp. Several transformations can be considered:
- Sublimation: transformation from a solid to a gas
- Vaporisation: transformation from a liquid to a gas
- Electroaffinity: the addition of an electron to a gas particle
- Dissociation: the separation of two atoms
- Ionisation: the liberation of an electron from a substrate
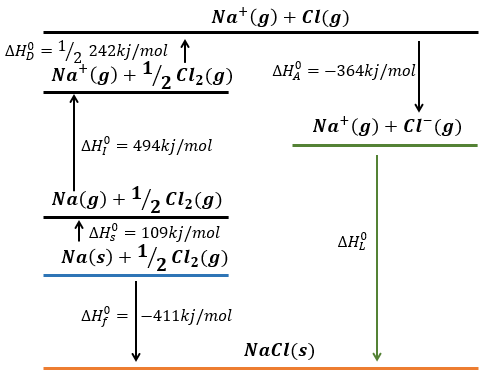
Let’s build the Born–Haber cycle for NaCl. We want to determine the enthalpy of this reaction:
To do so, we start from a reaction with a known enthalpy. We know that the enthalpy of reaction to form the solid from Na(s) and Cl2(g) is
The transformation from Na (s) to Na+(g) is made in two steps: first the sublimation of the solid into a gas
And then the ionisation of the gas
There are two steps as well to obtain Cl–(g) from Cl2(g). The first step is the dissociation of the two atoms of Cl2. As we only need one atom of chlorine, the enthalpy of dissociation is divided by 2.
The second step is to add an electron to Cl(g) (electroaffinity)
This energy is heavily negative because the chlorine reaches the octet. Now we have the two gaseous ions. We just need to add the enthalpy of all the steps together to obtain the lattice energy. The Born–Haber cycle is often represented this way:
Chapter 7 : Solids – crystallography
A characteristic of the solids is that they have their own shape. Liquids are taking the shape of their recipient and gases take all the available space. So solids have their own shape but some are malleable, can be cut, be creased or smashed or can be very rigid. As explained at the beginning of the chapter, all is a question of interactions between the elements of the solid.
There are different types of structure for solids:
Amorphous: disordered arrangement of the atoms
Crystalline: ordered arrangement of atoms. In a monocrystal, the whole solid grew from one point and there is a single arrangement. However, it is difficult to obtain a monocrystal because several growth point can develop simultaneously crystals with different orientations. Several crystals can grow in different directions and coexist in one solid.
Ceramic: some crystals in an amorphous network. It is a melange of the two previous types of structure.
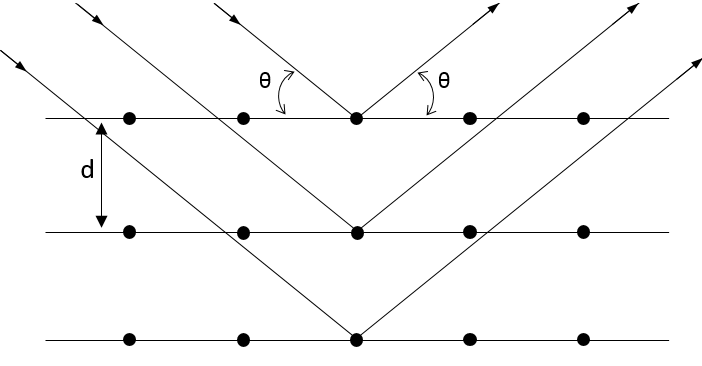
The structure of a solid can be determined through the diffraction of X rays.
The solids can be made of different types of liaisons:
Metallic: electrons can move along the solid. They are very compact and show identical properties in all the directions
Ionic: anions are surrounded by cations and vice versa. In the case of spherical ions, the properties are identical in the three directions.
Covalent: electrons are localised between the nuclei, in the liaisons between atoms. The atoms cannot move freely. It is less dense than ionic or metallic solids because of the imposed liaison length and orientation.
Molecular: there is no specific rule to bind. In molecular solids, the molecules can move easily.
Crystal lattices
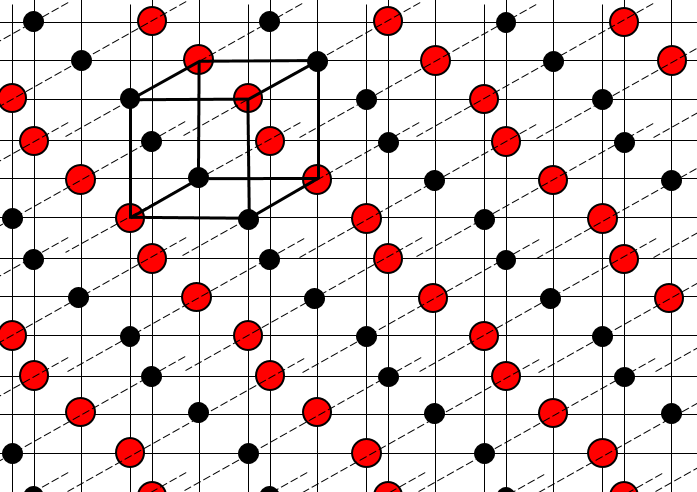
The structure of crystals can be defined through the smallest repeatable constituent of the network. NaCl is an ionic solid. Each Na is surrounded by 4 Cl and vice versa. The smallest repeatable constituent of the network is a cube made of 4 Na and 4 Cl, the atoms being in the corners of the cube.
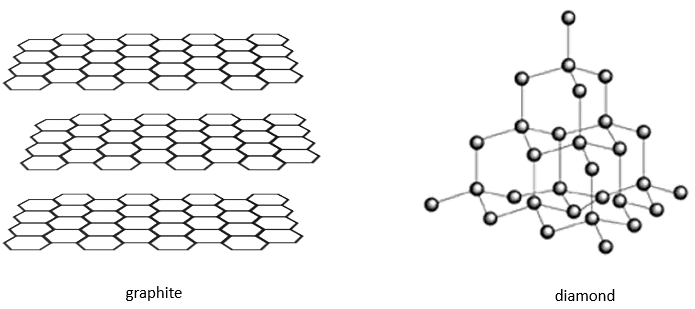
There are different base structures for solids. In general, one compound means one crystalline structure. Crystals of salt NaCl have a cubic structure. Carbon can have two different structures: the graphite (hexagonal) and the diamond (face-centred cubic). In the graphite, there are weak interactions between the sheets of carbon, making them easy to separate.
While the atoms are the same, the properties of the diamond and of the graphite are very different. Diamonds don’t conduct electricity, don’t break and are translucent. Their colour and opacity depend on impurities. Graphite conducts electricity (the electron of the orbital p are not bound and can move along the planes), break (planes can slide on each other) and are opaque.
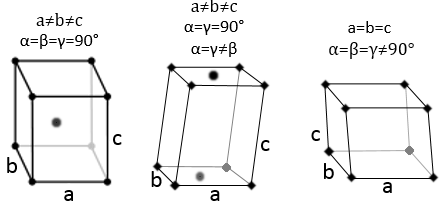
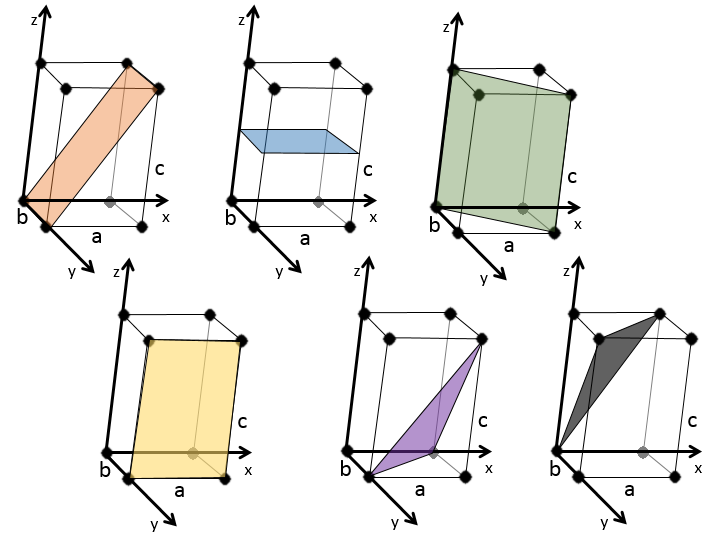
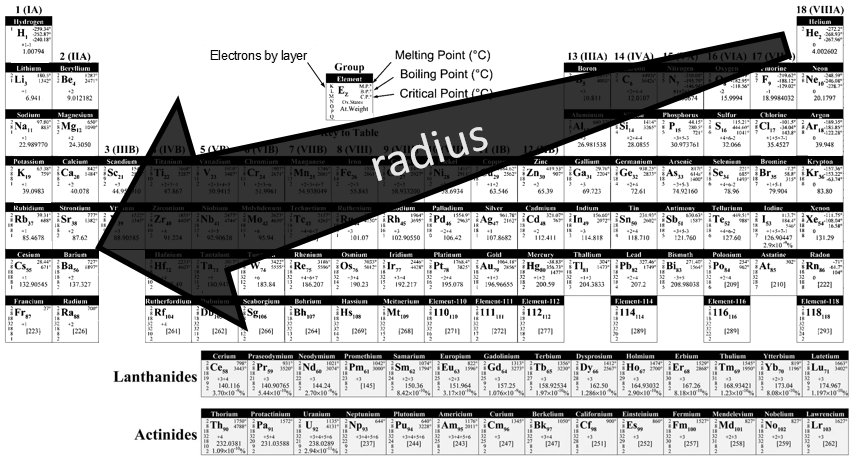
3 parameters are to be considered to sort the crystals: the lengths of the sides (a, b and c) of the structure, the angles between the sides (α, β and γ) and the position of the atoms in the structure. The geometric parameters give 7 lattice systems, given bellow while the position of the atoms sub-sorts them in 14 Bravais lattices
The different types of structures are:
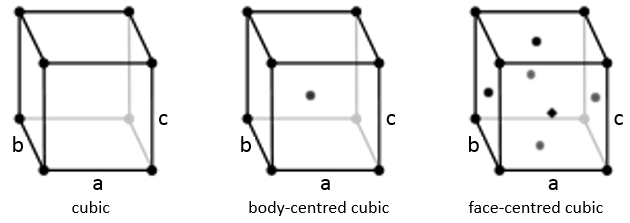
Cubic
In the cubic structure, the lengths of the sides are equal, a=b=c and α=β=γ=90°. If one atom is in the middle of the cube, we call this structure body centred. If one atom is in the middle of each face, we call it face centred.
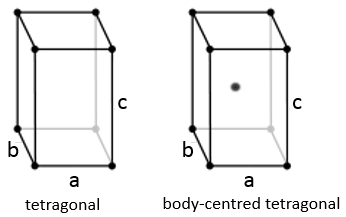
Tetragonal
When one side has a different length than the two others (a=b≠c), the structure is called tetragonal. The body-centred also exists for this structure.
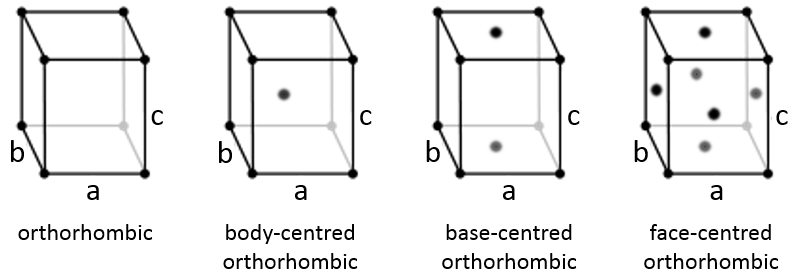
Orthorhombic
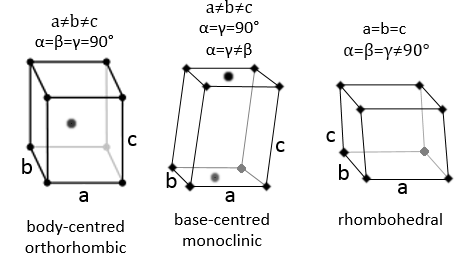
The angles are still 90° but none of the three characteristic lengths are equal (a≠b≠c). In the case of orthorhombic structures, an additional structure exists: the base-centred structure. In this structure, two opposite sides exhibit an atom at their centre. The other two sides do not.
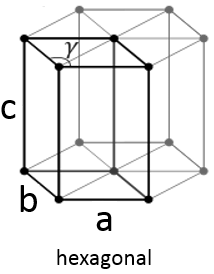
Hexagonal
This structure is called hexagonal but none of its face is hexagonal. However, if you assemble three of them you obtain a hexagonal prism. The base and top sides are diamond-shaped (a=b) with an angle γ=120°. The other faces of the structure are rectangular (a=b≠c) or cubic (a=b=c).
Rhombohedral
As for cubic structures, a=b=c and the angles are equal but in a rhombohedral structure they are not right: α=β=γ≠90°.
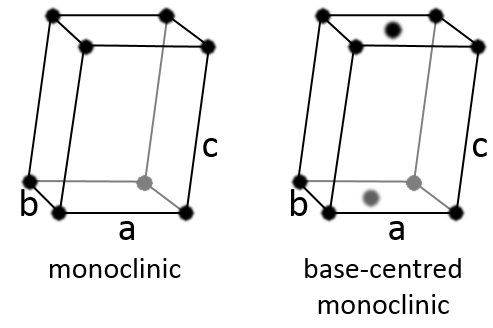
Monoclinic
In this case, two angles are equal to 90° but the third angle is not right. The sides have different lengths a≠b≠c.
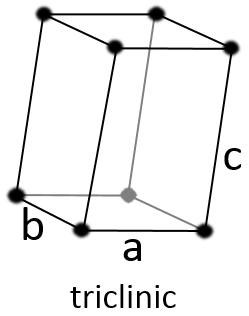
Triclinic
The angles α≠β≠γ≠90° are different and there is no right angle. Also, the lengths are different a≠b≠c.
Atomic Packing factor
It is determined by the ratio of the volume of the atoms in the crystal and the total volume
Considering spherical atoms, a portion of the cube is inevitably empty. The figures above are schematic and in a real solid, the liaisons are not so long. We would see something like this instead:
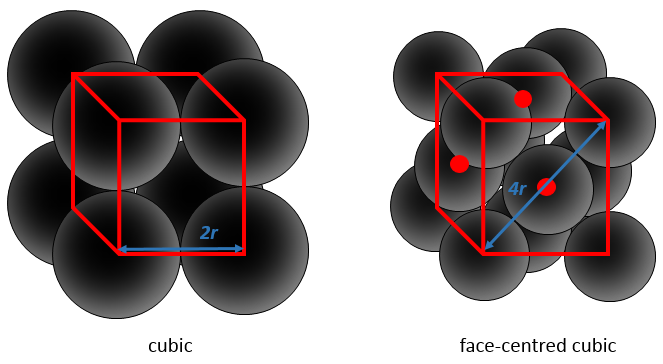
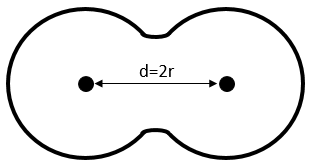
This proportion varies from one solid to another one. As an example, let’s consider a face-centred cubic structure wherein all the atoms have the same size, the same radius r. The length of the cube is a and is volume is thus a3.
The length of the diagonal is 4r, and from Pythagoras’ theorem, the square of the hypotenuse equals the sum of the square of the other two sides of a triangle. As a result,
We know the total volume of the cube
We just need to determine how many atoms are in the structure. In each corner of the cube, there is 1/8 of an atom. There are 8 corners, so there is the volume of one atom in total for the corners. At the centre of the faces, there is the half of an atom. There are 6 faces so that makes 3 additional atoms. In total, there are 4 atoms in the cube. The volume of one atom is 4/3 pi r3. The APF for this face-centred cubic is thus
For this particular structure, approximately one fourth of the cube is empty. It is the same for the hexagonal structure, reaches one third for the body-centred cubic and one half for the cubic.
- Hexagonal close-packed: 0.74
- Face-centred cubic: 0.74
- Body-centred cubic: 0.68
- Simple cubic: 0.52
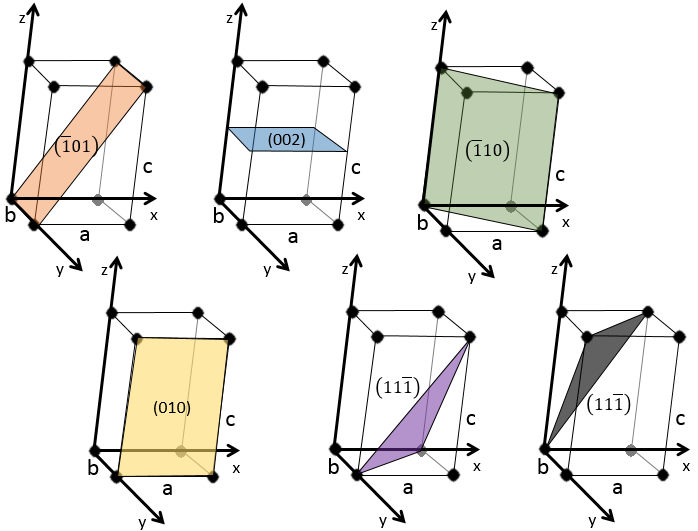
Miller indices
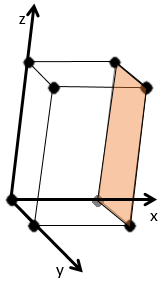
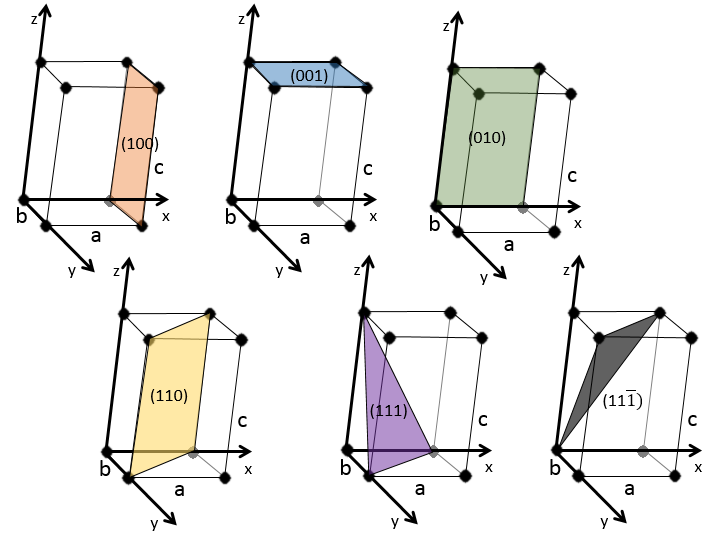
Miller indices form a notation system for planes in crystal lattices. It is mainly used in crystallography but I did not used it a lot myself as a chemist. I won’t develop it intensely here. The Miller indices are a trio of 3 integers, written (hkl). Considering one corner of a crystal structure, let’s say a cubic one, as the base (000) of the notation, the axis are following the sides of the crystal. This base is thus not always orthogonal if one of the angles α, β and γ is not right. In the case of a cubic structure, the base is orthogonal.
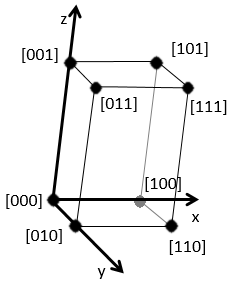
Moving in the x direction, we will find an atom after a distance a=2r. It is the same if we move in the y or z directions. For the Miller indices, the coordinates x, y and z are divided by the structure dimensions a, b and c respectively.
The atom on the x axis is on the location [100] (it is not a Miller index, just a coordinate). The atom on the y axis is on [010] and the atom on the y axis is on [001].
The Miller indices (hkl) describe a plane by telling where they cross the axis x, y and z. Considering the following plane
We see that it is parallel to the y and z axis and that it crosses the x axis at x=1. As the plane is parallel to y and z, they will never cross. We consider that it would be done at y=∞ and z=∞. To obtain the Miller indices, we take 1 over these values:
If negative values are used, we overstrike them instead of putting a minus sign.
Some examples of planes are next
Exercises
1. How do you call these structures?
2. Give the Miller indices of the following planes:
3. The density of the solid NaCl is 2.165. What volume is occupied by 1 mol of it?
4. Calcium has a fcc configuration. The length of one side of the cube measures 0.557nm. What is the radius of the calcium, the filling ratio and what is the density of this crystal?
Answers
1:
2:
For the first one, the showed plane passes by the y axis. Consequently we have to translate it. By default, we translate it following the x axis by one length a to the left.
For the second one, the plane is placed on the middle of the structure, horizontally. Remember that we take the inverse of the position: 1/0.5=2.
As for the first one, the third plane passes by an axis. We translate the plane to obtain the correct answer.
The two last planes have the same Miller indices. They are parallel and merge if we apply a translation in the z direction.
3.
4. The structure is fcc (face-centred cubic) so our point of reference is the diagonal: its length is 4 times the radius of one atom.
To know the density, we calculate the volume of 1 mol
Chapter 6 : Liquids
Liquids
Liquids are a condensed state: the volume of a liquid does not change by much when a pressure is applied. A liquid is a fluid: it has not its own shape and molecules can move inside it. As said previously, liquids are characterised by a short range order and a long range disorder.
Properties of liquids
Superficial tension
When a droplet of water falls on a metal surface (for example), the droplet does not spread completely. The droplet is not a monolayer of water but has still a characteristic shape and a width.
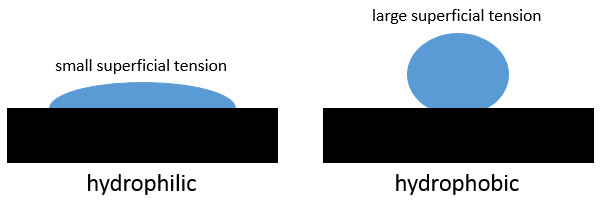
The shape depends on the interactions between the molecules of the liquid between themselves, their interaction with the molecules of the surface. If the interactions with the surface are stronger than the intern interactions of the liquid, then the droplet spreads on the surface. The surface is said to be hydrophilic if a liquid spreads on it. On the opposite, on a hydrophobic surface, droplets remain in a spherical shape (it is possible to almost have a complete sphere). If the surface is inclined, the droplet will just roll on the surface. With a designed surface, it is possible for a droplet to climb on an inclined surface shaped like a stair (Enhanced Droplet Control by Transition Boiling, Alex Grounds, Richard Still & Kei Takashina, Scientific Reports 2, 720)
The superficial tension is a property of the liquid while the hydrophobicity is a property of the surface.
To increase the surface (by ΔS) between a liquid and a solid, a work W is required
γ is given for a type of surface, so that it only depends on the interaction between the molecules of the liquid. A small superficial tension means that the liquid will easily spread, that the work to increase its surface with the solid is small. Oil for example spreads easily on a surface. On the contrary, the mercury has very strong metallic bonds and minimises its surface with the solid. It keeps a spherical form.
Capillarity
It is the ability of a liquid to flow in narrow spaces without external forces, or in opposition to external forces. Typically, if you partially plunge a piece of paper in water, water will move upwards on the paper, despite the influence of the gravity. The capillarity is the resultant of several forces: the adhesion force between the liquid and the surface against the weight of the liquid and the cohesion force in the liquid. On the paper, the water will stop to move upwards when those forces are cancelling each other.
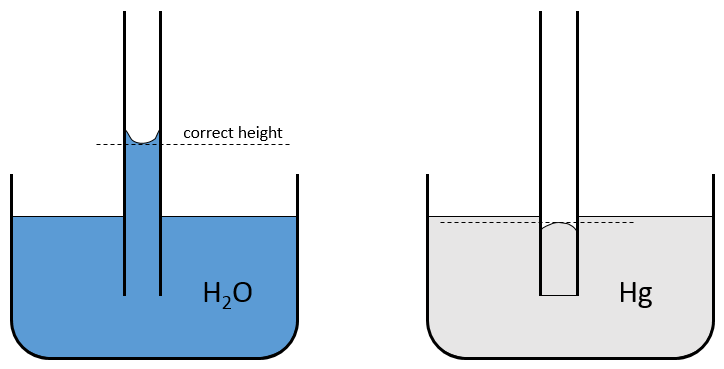
In a tube of glass, the adhesion force is important because the glass possesses O– anions which favour the adhesion. Consequently most of the inorganic liquids climb in a tube, we can see that the surface of the liquid is generally not flat but incurved. It is called the meniscus. The adhesion energy is favourable enough to increase slightly the water-air surface so that the height along the wall is greater than in the middle of the tube. The difference of height can be several millimetres. On a graduated tube, the height to consider is the one in the middle of the tube.
When the adhesion force is smaller than the cohesion force, the level in the tube will be lower than the level of liquid out of it. It is the case for the mercury. Its meniscus is also different from the meniscus of the water as the mercury avoid the contact with the surface.
Chapter 5: The states of matter: Gas
The states of the matter
We can consider 3 different states –gas, liquid and solid– and a melange of them. One important difference between the three states of the matter is the volume they occupy. A gaz takes all the available space, a liquid takes the form of its recipient and a solid has its own form. It is the result of the interactions between the molecules composing the matter. The composition matters but it is not the single parameter to considerate. Simply set, the composition of water, ice and vapour of water is the same (H2O), but the interactions between the molecules of H2O are different. Sometimes things are not totally a solid nor a liquid nor a gas. An example is the shaving foam: it has not its own shape but does not completely take the shape of its recipient. Generally, in this case we are in presence of a melange of two cohabitating states. The goal of this chapter is to describe the different states of the matter and the transitions between them.
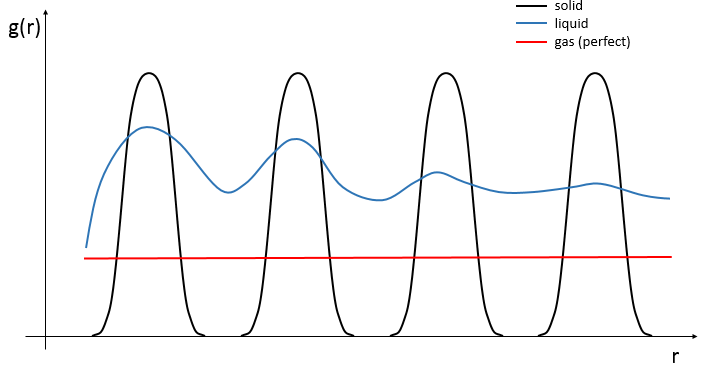
The arrangement of the matter can be defined from the repartition of neighbour atoms between them. If we focus on one specific atom, the probability g(r) to find one or many atoms at a given distance r of the atom differs strongly between liquids, solids and gases.
In a solid, the atoms are organised and don’t move freely (they can vibrate around their position). The repartition depends on the geometry of the solid but it is characterised by high, localized peaks at regular distances with g(r)»0 between them. In a liquid, we can see that there are still layers of neighbours around a given atom but that the order is less important. Moreover, the peaks vanishes after a few layers. A liquid is thus characterised by a short range order and disorder at long range. The average number of neighbours in a liquid is in general smaller than in a solid. In a perfect gas, the atoms don’t feel each other and have no interaction. The probability to find an atom at a given distance of another one is thus equal at any distance. In real gas however, interactions can exist and g(r) varies slightly.
Gases
We are surrounded by gases. We can displace them when we are moving but they apply a resistance to our moves. Even when we are not moving, there is a pressure of the air on us. We don’t feel it because we are used to it and our body applies a force to counter this pressure. If the void was made, we would expand because of this force. The fact that air applies a pressure has been proved by Otto Von Guericke (XVIIth century). He build two half spheres, fitting each other. He removed the air from them and asked to his lord to try to open it with the help of four horses. They did not success. Putting back air into the sphere, it was possible to open it again.
There are still objects that we often use based on this principle: suction pads for plumbing, the ones to put your GPS on the windscreen. The void that we create is never complete and the strength necessary to remove a suction pad depends on the degree of void that we created. It becomes way easier to remove them once we allowed a bit of air to get in the suction pad.
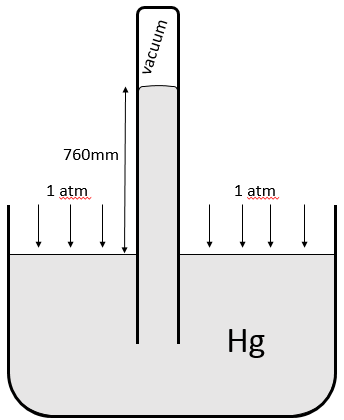
A pressure is a force applied on a surface. The pressure applied by the air in standard conditions is 1 atmosphere, which equals 101325 Pascals, more usually given in hectoPascals (1013hPa). We also measures the pressure of a gas with torr. 1 atm=760torr. The torr unit is the height, in mm, that mercury reaches in a voided tube when a pressure is applied on the rest of its surface in the following disposition.
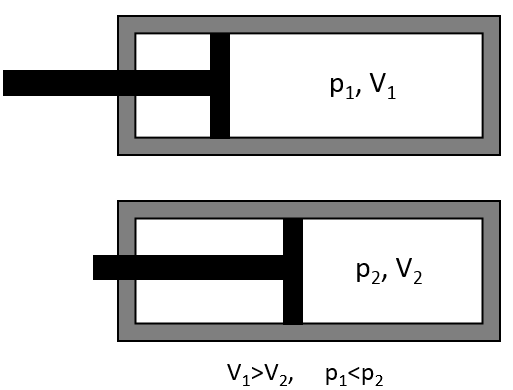
There is a relation between the volume of a gas and its pressure. Boyle determined that at a constant temperature, the multiplication of the pressure of a gas by its volume gives a constant.
If the volume decreases, the pressure increases by the same ratio:
Charles Gay Lussac observed on the other hand that the volume of gas depends on the temperature and that, does not matter the gas, its volume trends to 0 when the temperature goes towards 0K (he extended the curves when the gas changes of state).
A third contributor to the understanding of the gases is Avogadro who said that at a given temperature and pressure, the volume of a gas is proportional to the number of atoms it contains:
k is the constant of Boltzmann. Considering all of that, the law of perfect gases was established:
This law is limited to diluted gases and we consider that the particles are punctual, distant and that there is no interaction between them.
If we consider several gases, Dalton showed that the total pressure is given by the sum of their individual pressures.
![]()
As a consequence, if we consider a melange of two gases
![]()
The individual pressure of one component of the gas is proportional to its concentration in the gas:
![]()
Kinetic theory of gases
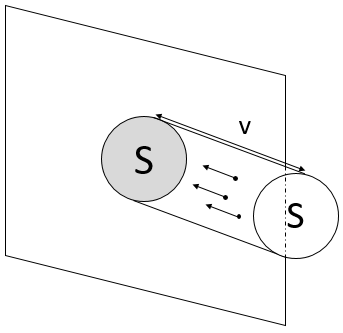
We can measure the pressure applied by a gas on a surface. As explained before, a pressure is a force applied on a surface. A force is a mass multiplied by an acceleration. An acceleration is the variation of speed over a time.
Note that only the component of the speed perpendicular to the surface affects the pressure. The two other components don’t have an influence on this particular surface.
We make several assumptions about the particles of the gas:
- The particles are small and their volume is negligible compared to the volume of the gas. They are considered as dots.
- They all have the same mass m,
- They have a constant speed and go in random directions. We can define an average speed <v>.
- The particles don’t interact together
- All the collisions are purely elastic: there is no loss of speed or energy
To determine the pressure on a surface S of one of the walls, we consider the particles that are able to hit this surface in a period of time dt. As a result, we only consider the particle present in a small cylinder in front of the surface.
When a particle hits the wall, there is an elastic collision and the particles goes back with the same speed. Over one period of time, the speed of a particles changes from v to –v. The force applied on the surface by one particle is thus
![]()
In the cylinder, there is a given number of particles:
N/V is the density of particle in the gas. Amongst them, only the particles going in the x direction are important for us, and amongst them only the particles going in the direction of the surface (not in the opposite direction) induce a pressure on the surface. A 1/6 multiplication is thus applied to determine the number of particles impacting the surface. The pressure is thus
![]()
In this equation, we recognise the kinetic energy Ek=mv2/2. Keeping in mind that N=n.NA, we can write
As a result, we see that the kinetic energy of particles in a gas is directly proportional to the temperature
From there, we also see that the average speed of the particles is related to their mass:
It means that in a gas at a given temperature, particles of oxygen and of nitrogen do not move at the same speed. For example, a balloon of nitrogen (N2, M=28) deflates faster than a balloon full of oxygen (O2, M=32)
This property is used to enrich uranium, i.e. obtain a larger proportion of one isotope of the uranium. Considering a volume of gas containing 235UF6 and 238UF6, a bigger proportion of 235UF6 will pass through a small gap because it has a larger speed than 238UF6. This process is the effusion: a separation based on the speed of the particles.
The heat capacity (at V=cst) is the energy required to increase the temperature of one mole of gas by 1° is
The heat capacity (at p=cst) is
In a monoatomic gas, all the energy is used to increase the speed of the particles.
Diatomic gases
For molecules of more than one atom, the kinetic energy is split up in the three directions (1/2R by direction).
If a diatomic gas is heated, the energy is used by several processes:
- translation/acceleration: the speed/kinetic energy of the molecule increases,
- rotation and vibration
There are two angles of rotation, the energy required to rotate is 2*1/2R
If the molecules vibes, they have a potential energy. The energy obtained from the heating is thus distributed in kinetic energy and in potential energy. The energy required to vibe is thus also 2*1/2R.
The values of Cv and Cp are thus higher than for a monoatomic gas:
So, if we give energy to Ne and N2, which gas should heat more? N2 uses the energy of the heating to accelerate but also to vibe and to rotate. Ne uses all the energy as kinetic energy and will thus heat more than N2.
Distribution of Maxwell-Boltzmann
The calculations we have done assumed that all the particles of a gas were affected identically by the heat. In reality, the heat capacity depends on the temperature but trends to 7/2R for T trending to infinite. The explanation follows:
Particles can have different levels of kinetic energy. When energy is supplied, not all the particles are equally excited. One proportion of their population increases its kinetic energy by one level (or more eventually). At OK (absolute zero), all the particles are at the lowest level and don’t move. They are frozen.
The population on the second level is given by
ΔE1 is the difference of energy between the level 1 and the level 0. k=R/NA is the Boltzmann’s constant. In general, the population is given by
The distribution of speed of the particles in the levels of energy are given by the law of distribution of Maxwell-Boltzmann. From above, we can determine that the variation of level with regard of the variation of speed
With A an undetermined constant. We can write this equation differently:
It is possible to integer this equation, knowing that
It would mean that A=(m/2πkT)1/2. However, the speed has three components. As a result, the distribution is
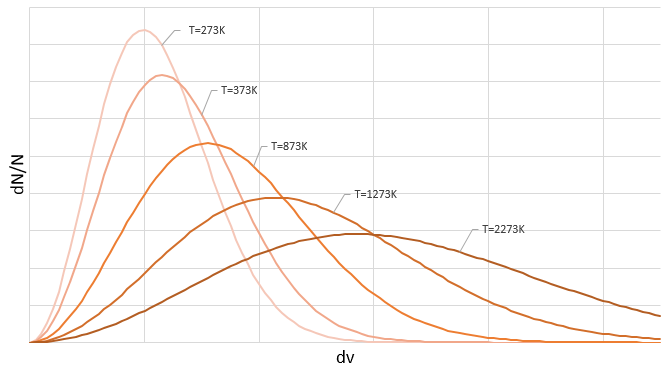
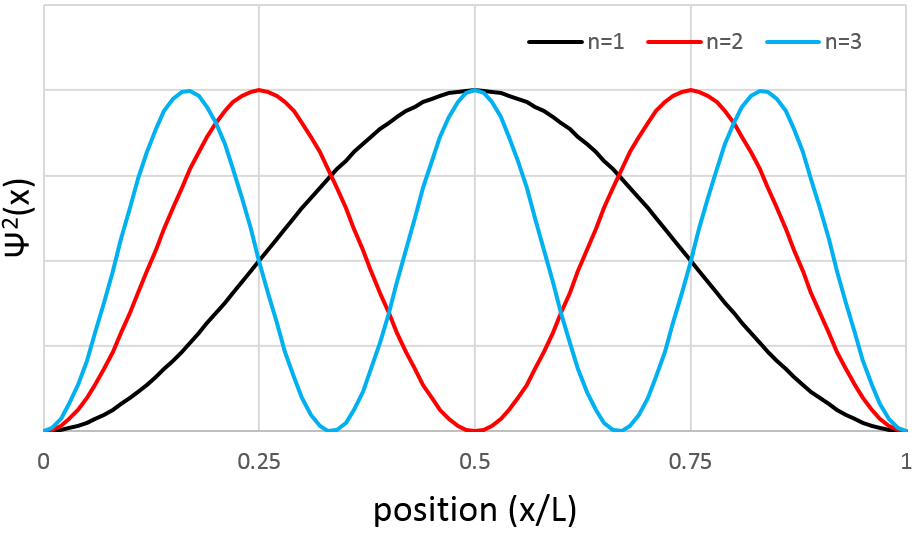
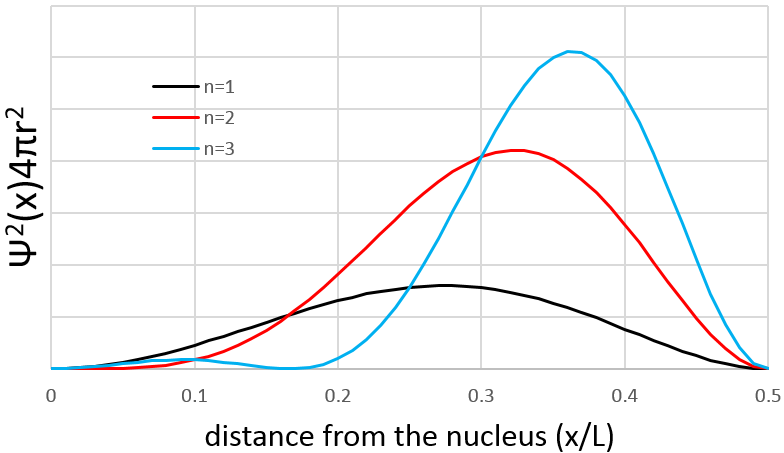
Similarly to the probability of presence of the electrons for the electronic orbitals, we integer on a sphere and we should multiply this equation by 4πv2. We have thus obtained the proportion of particles dN on the total number of particles N with a given speed dv.
One can see on this figure that the average speed increases with the temperature, as it was determined previously in the relation
from the law of perfect gases. The most probable speed is found at the maximum of the curves, when dN/N/dv=0, i.e. at
The average speed that we find is a bit smaller than the one obtained from the law of perfect gases:
Real gases
The law of perfect gases works well for diluted gases. If we increase the pressure or the temperature of gases, we see deviations from the law of perfect gases.
It is because the number of interactions between the particles becomes less negligible. The interactions can be attractive or repulsive but are weak with regards to the energy of a liaison for example. The interactions can be between induced dipoles or between permanent dipoles:
Interaction permanent dipole-permanent dipole
In this case, the molecules composing the gas already possess a dipolar moment. The δ+ and δ- charges of molecules passing near each other interact: an attraction is induced between opposite charges and repulsion between dipoles of same charge.
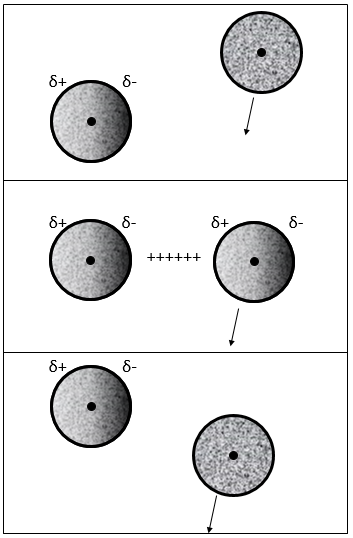
Interaction induced dipole-induced dipole
The electrons near a nucleus are, statistically, equally distributed around the nucleus. In other words, the cloud of electrons is spherical and the density of electrons is identical in all the directions. However, the electrons are continuously moving and heterogeneities of charge may appear temporarily. In fact the apparition of these dipoles is frequent but in average the dipolar moment is cancelled.
When an atom passes near another atom showing a dipole, the atom adapts its electrons cloud to the dipole to reduce the repulsion between them.
In general, the interactions are favourable between the particles of a gas. The particles tend to remain close of each other, decreasing the pressure with regard of a perfect gas.
On the other hand, the particles have a proper volume and the other particles cannot penetrate this volume. In the law of perfect gases, the particles were considered as dots, with a negligible volume.
As a result, despite the increase of interactions, the pressure increases faster than for a perfect gas.
Instead of the perfect gas law PV=nRT, we have to consider the van der Waals equation for real gases:
In the pressure term, the +a(n/v)^2 expresses the interactions between the particles. a stands for the interaction strength, the value of which depends on the type of interactions, the size of the molecules, the number of electrons, etc. (n/V)^2 stands for the “density” of interactions and should in fact be n/V*(N-1/V) as each particle of the volume (n) can interact with all the other particles (n-1) but as n is proportional to NA, the difference is negligible.
In the volume term, b stands for the covolume of one particle. The empty volume where particles can move is the total volume minus the volume of the n particles composing the gas.
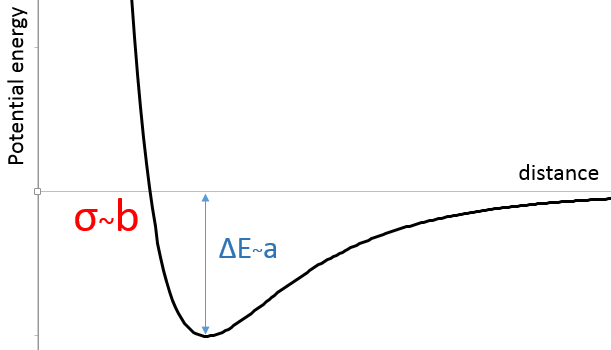
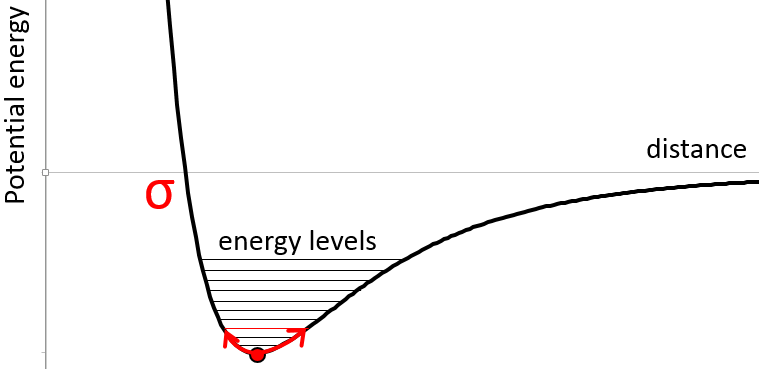
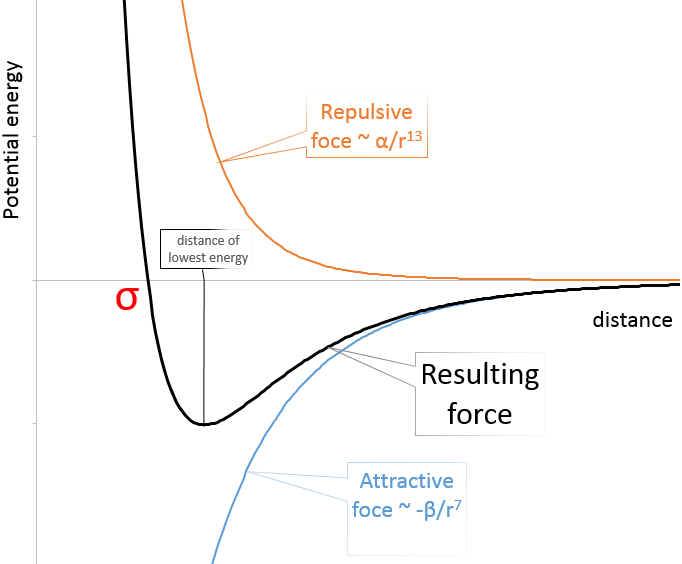
In the figure of the potential of Lenard Jones, we can relate a and b to the energy of the pit and to the distance of smaller approach σ.
The enthalpy of vaporisation ΔHv reflect the energy required to transform a liquid into a gas. It requires more energy to vaporise molecules with strong interactions than molecules with only induced dipoles. Sprays of water are sold because of this property: once on our skin, the small droplets vaporise, taking the energy from the skin, decreasing its temperature and giving a feeling of freshness.
The opposite process is the liquefaction. The molecules in the gas are distant from each other. To become liquid, the particles move into the potential pit. However if they have a too large kinetic energy (depends on the temperature), they will get away from the other particle. It takes energy to leave the potential pit. As a result, liquefaction involves a decrease of the temperature.
Exercises
1. What is the volume of 1,5g of N2 under a pressure of 1atm, at 20°C?
2. What is the total pressure of a gas composed of 120g of H2 and of 80g of He if the temperature is 25°C and the volume is 300l? Express your answer in atm, Pa and torr. What in a volume of 450l or 600l?
3. What is the required volume of oxygen to burn 1g of butane (C4H10)? Knowing that all the products are gaseous, what will be the volume after the complete combustion?
4. Considering that the combustion of 1g of a gas composed of CH4 and C2H6 formed 1568ml of CO2 and water at 18°C and 742torr, what are the masses of CH4 and C2H6 of the sample?
5. To produce a neon lamp of 520cm long by 2cm of diameter, the pressure inside the tube has to be equal to 1.5mm Hg at 37°C. Determine the mass of neon required to obtain those conditions.
6. A recipient of 500ml is filled with CO2(g) at the pressure of 1 atm at 20°C. What is the mass of the gas? What is the pressure if we increase the temperature by 40K? What is the pressure if we next compress the gas to a volume of 100ml?
7. Sort the following systems from the closest to the farthest of a perfect gas:
a)H2 at SCTP
b)He at 350K and 1 atm
c)H2 at 273K and 2 atm
d)He at SCTP?
8. Compare the results of the equations of the perfect gases and of Van der Waals (a=4.17l2/mol2, b= 0.0371l/mol) for a volume of 20l, 2l and 0.2l containing 1 mol of NH3 at 0°C.
9. Considering that the minimum of the function of Lennard-Jones for the argon is at -996J/mol at a distance of 0.382nm between the atoms, what would be the potential at a distance of 1/2×0.382nm, 2×0.382nm and 3×0.382nm?
10. What is the kinetic energy of 1 mol of Ne at 20°C and 1 atm. What are its heat capacity at a constant pressure and at a constant volume? What is the difference if instead of neon we had nitrogen?
Answers
1. We use the law of perfect gases to solve this problem
2.
3. The first step is to determine how many moles is 1g of butane:
Now we write the chemical reaction to find the stoichiometric coefficients
The required volume of oxygen is thus
9 moles of gas are produced by the reaction per mole of butane, so the volume after the reaction is
4. The reactions of combustion are
We know that 1g of reactants give 1568ml of CO2. The molar masses of the reactants are
In 1g we have n1 moles of CH4 and n2 moles of C2H6
As we have the volume, the pressure and the temperature of the CO2, we can determine how many moles of CO2 are produced by the reaction with the law of perfect gases
The pressure has to be put in the IUPAC units (atm) instead of torr: 1atm=760torrà 740torr=0.974atm and the temperature is put in Kelvin (°C+273.15)
1 mol of CO2 is produced for each reaction of combustion of CH4 and 2 are produced by each reaction of C2H6. The total amount of CO2 is thus equal to
We have two equations with two unknowns to solve. To do so, we can insert the expression of x into the first equation
The masses are thus
5.
6.
7. b-d-a-c
8.
9.
Diatomic gas:
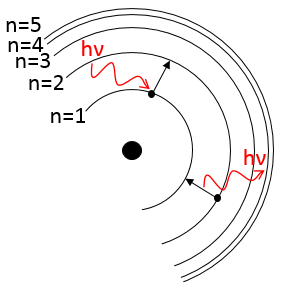
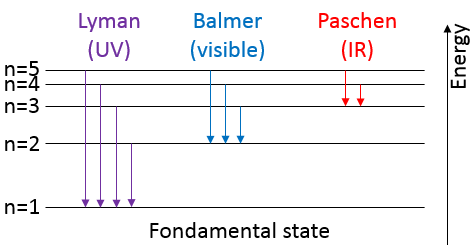
Chapter 4: Redox reactions
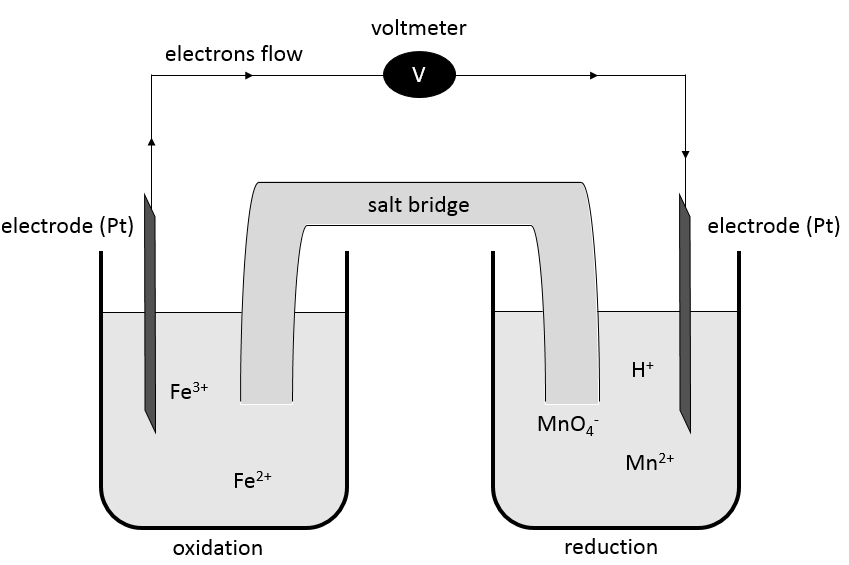
Oxido-reductions, or redox, are reactions involving a transfer of charge between molecules. During such reactions, some chemical energy is transformed into electrical energy.
An oxidation reaction is a reaction during which a substrate (molecule, atom or ion) loses electrons.
A reduction reaction is a reaction during which a substrate gains electrons.
An oxidant is a substrate with the ability to oxidize other substances. During this process, the oxidant is thus reduced. They are also called oxidizer or oxidizing agent.
A reductant is a substrate with the ability to reduce other substances. During this process, the reductant is thus oxidized. They are also called reducer or reducing agent.
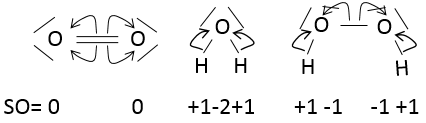
The state of oxidation
The state of oxidation (SO) is an integer the value of which is the charge of an atom if we break all its liaisons. In O2, each atom takes its electrons back (it is a homolytic cleavage or homolysis). The global charge of O2 is neutral. Thus the SO of each oxygen is 0. However, in H2O, the oxygen takes the electrons from the hydrogen’s when we break the liaisons because the oxygen is more electronegative than the hydrogen (it is a heterolytic cleavage or heterolysis). The SO of oxygen in H2O is -2 and the SO of the hydrogen’s is +1.
In general, the SO of the oxygen is -2 and we can find the SO of the other atoms of the molecule without the full representation of the molecule. For example, we can determine the state of oxidation of the manganese in MnO4–: the global charge is -1 and each oxygen has a SO of -2. The SO of Mn is thus +7 so that the global charge equals the sum of the states of oxidation -1=+7-(4x-2). In heavy water, H2O2, the SO of the oxygen’s is -1.
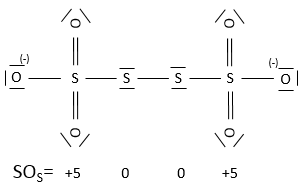
An atom can thus have several possible SO. If several SO are present for one atom in a single molecule, we take the average between them. For example, S has a SO of +2.5 in S4O62-. Sulphur can have a SO from 0 (solid sulphur) to +6 (H2SO4).
Redox reactions
So, in a redox reaction, an oxidant oxidizes a reductant while the reductant reduces the oxidant. In presence of two compounds, it is however not always obvious to determine the direction of the reaction
This reaction involves two half reactions:
The reaction will go in the direction that has a negative enthalpy. In the present case, the reaction goes from left to right and it can be explained because Cu is more electronegative than Zn. It is thus harder to take its electron from Cu than from Zn.
It is possible to determine the strength of the oxidants and reductants from their ability to attract electrons in a battery, i.e. their standard potential ε0 (in volts). However, an absolute value of the standard potential is not measured. We can only know the value of ε0 with regard to another couple. We use the couple H+/H2 as a reference, with its standard potential set to ε0=0.000V in sctp by convention. The name of a couple is put in the direction of the reduction: oxidant/reductant. For example: Cu2+/Cu, Zn2+/Zn.
To establish a redox reaction correctly, a method exists:
First, we write the supposed equation without stoechiometry, protons, water or OH–. Just the oxidants and reductants. We determine their state of oxidation
Second, we determine the individual standard potentials of each couple. The values of ε0 can be found for a large range of compounds on the back of Mendeleev tables. It is given for the reduction reactions (for the oxidation, take the negative value). For the iron, the reaction is
For the manganese, 5 electrons are added to obtain Mn2+.
Be careful to consider how many atoms are reduced/oxidized. In the couple Cr2O72-/Cr3+, Cr has a SO of +6→+3 but 6 electrons have to be added in the reaction because two Cr are reduced.
Coming back to the problem involving manganese, the reaction is not balanced yet. Oxygen’s are also involved in the process. We balance the reaction with water molecules, protons or OH– depending on the acidity of the solution. To determine how many species are required, we count the charges at each side of the arrow:
There are 6- at the left because MnO4- is negatively charged. The difference of 8 charges is balanced by the addition of 8 protons at the left of the arrow and we balance the equation:
The standard potential of this reaction is known. Now, we put together the two half reactions. Don’t forget to consider that one half reaction introduces 5 electrons and the other one introduces 1 electrons. The equation of Fe3+/Fe2+ is thus multiplied by 5.
This final reaction is correctly balanced. Note that even if the half reaction Fe3+/Fe2+ is multiplied by 5, it is not multiplied in the determination of the standard potential. As Δε0>0, it means that the reactions goes from left to right. This reaction is spontaneous if the production of enthalpy ΔG0<0. The enthalpy of reaction is a measure of the work required to do the reaction. If this value is negative, the reaction is spontaneous and liberates energy, generally in the form of heat. The reaction is said to be exothermic. If this value is positive, it is necessary to give some energy to do the reaction. The reaction is endothermic as it absorbs heat from its surrounding.
The relation between the enthalpy of a reaction and its potential is
This relations comes from the fact that a potential V is the variation of work J to modify the charge Q
Batteries
In batteries, the elements of a redox reactions are separated. The two solutions are connected by a salt bridge and two electrodes connected to a voltmeter.
A salt bridge is a device used to connect two half batteries, that is full of ionic species conducting electricity (electrolytes) but not interfering with the compounds of the battery. Without the salt bridge, one half cell would accumulate negative charge and the other half cell would accumulate positive charge as the reaction proceeds. The cations and anions of the half bridge are chosen so that they have a similar high conductivity. KCl, KNO3, NH4Cl are some examples of electrolytes composing a salt bridge.
A battery is written by convention as follows:
The electrodes are put at the extremities and the compounds of the two half batteries are separated by a double line symbolizing the salt bridge. The oxidation is put in first and the reduction in second.
The oxidation of Fe2+ is done at the electrode of platinum that catches the freed electron. This electron goes through the voltmeter to the other half battery where it is used in the reduction. The salt bridge closes the electric circuit.
The potential of a battery, also called electromotive force, is given by the Nermst equation and depends on the concentrations of the different species:
We can also obtain the potential from the difference between the two cells of the battery:
Be careful that the concentrations of Fe2+ and Fe3+ were inverted in the last equation because we consider the products and reactants of the half batteries in this case.
In a battery of concentration, the electromotive force is only given by the concentrations of the species:
The two sides of the battery have the same ε0 and the equation for the electromotive force is thus limited to
Here, we cannot use KCl as electrolyte because Cl– would react with Ag+ to form a precipitate of AgCl.
Electrodes of reference
An electrode of reference is an electrode the potential of which is known and does not varies during an experiment. The standard hydrogen electrode (SHE) is a first electrode of reference but is not often used because it is not entirely reproducible.
Dihydrogen gas is introduced in an acid solution of 1M with a pressure of 1atm.
The silver chloride electrode is used as electrode of reference
The potential of the electrode depends on the concentration of the ionic form of Ag.
However, this concentration also depends on the solubility of AgCl in water
The constant of dissolution of AgCl is KS=[Ag+][Cl–]. By saturating the solution with KCl (>3.6M), the concentration of chloride is constant, hence the fixed concentration of Ag+.
The potential written above is not totally correct because at large concentrations, the concentration is no more equal to the activity of an ion.
The saturated calomel electrode uses the same principle:
Here the mercury cations precipitate with chloride which is saturated the same way as for the silver chloride electrode
The reverse of a battery is the electrolyse: a current is applied in a cell to induce a reaction with a negative electromotive force. It is a way to depose metals from a solution.
The quantity of deposed metal depends on the applied current:
All the first column of the Mendeleev table are obtained by electrolyse. In the nature, they exist in their oxidised form because the world is oxidant: H2O and O2 are everywhere. The production of Na can be done from its salt by electrolyse:
This reaction is performed at high temperature (>600°C) and in total absence of water.
Disproportionation
In some cases, a single species plays simultaneously the role of oxidant and reductant. A reaction involving such a process is called disproportionation. The salt of copper dissociates in water in Cu+ and Cl-. However solid copper is obtained during the process. It is a consequence of the disproportionation of copper:
As the second reaction has a larger potential, the global reactions forms solid copper:
The Cu+ dissociated from CuCl forms spontaneously Cu2+ and Cu(s).
Monoxide of carbon is the result of disproportionation between CO2 and C. It is a process responsible of many incidents, often lethal, in bathrooms with an insufficient ventilation. Traces of carbon, obtained from burned organic compounds, reacts with the carbon dioxide emitted by boilers or heaters. The problem is that CO takes the place of O2 on our blood cells and is much strongly bound to them than O2 (by a factor 200). Once CO is bound to a blood cell, O2 can difficulty bind, Because of that, only a small proportion of CO can be catastrophic. To treat people affected by CO, they are placed in a room overpressured with O2 to force the equilibrium and remove the carbon monoxide.
The standard potential of a reaction can be found from its intermediate reactions.
In total, 3 electrons are required to obtain the iron on its solid state. 1 electron is required for the first step and 2 for the second step. The (approximate) standard potential is found by a combination of the standard potential of each step, taking in account the required electrons for each step:
In total, the process has a negative standard potential. The reverse reaction is thus spontaneous in presence of an oxidant. It is the production of stain (hydrated Fe3+) from iron. On a car for example, the iron is protected by a thin layer of painting/coating, not allowing water to the contact of the iron. If there is a default on the coating, the iron is oxidised but the stain will not always appears at this location: the electrons freed by the oxidation can move through the metal.
To avoid this, surfaces are connected by an electric cable to a piece of zinc. The zinc will oxidise instead of the iron because its standard potential is smaller.
Stain is a porous material and the oxygen can pass through it to proceed further. ZnO is not porous so a monolayer of Zn can protect iron pieces from stain. It is the principle of stainless iron, but applied with Cr2O3.
Chapter 3: Liaisons and molecular orbitals
Atoms make liaisons because they get more stability. A proof is that to break a liaison, we need to give energy to the molecule.
Atoms in a molecule are at a given distance, and oscillate slightly from this position depending on the energy they receive.
The atoms cannot oscillate at any frequency. There are authorized levels of energy at which the atom can be placed.
Even at n=0, the fundamental state, the atoms oscillates at a given frequency.
It is difficult to approach more the atoms from each other but it also requires energy to pull them away. The dissociation energy is the energy required to separate two atoms by an “infinite” distance.
To form a liaison, the clouds of electrons around the nuclei concentrate between the two nuclei to shield their charge and decrease the repulsion between them. The repartition of electrons differs depending on the type of liaison. New orbitals, molecular orbitals are formed from the atomic orbitals to bind two atoms.
Only the last layer of electrons, the electrons of valence, is taken in account for the molecular orbitals: the inner layers are too distant to interact.
4 types of liaisons exist: covalent, ionic, metallic and coordinative liaisons (or hydrogen bridges). We will develop the two first types of liaison here
Covalent liaisons:
Such a liaison is made between atoms of same electronegativity (or almost). Each atom put one electron in common to make a covalent liaison. The electrons in the liaison are shared equally along the liaison.
Ionic liaisons:
Such a liaison is made between atoms of different electronegativity. In an ionic liaison, the electrons are not shared equally. One atom is the donor of electrons and the other is the acceptor of electrons. The acceptor is more electronegative than the donor.
As the electrons are not equally shared, a gradient of charge exists along the liaison. We say that there is a dipolar moment.
Polarity
H and F have different electronegativities (2.1 and 4 respectively). Most of the electrons of the liaison are thus closer to the atom of fluorine than to the atom of hydrogen.
The dipolar moment μ of this liaison can be defined as
By definition, the dipolar moment goes from the positive charge to the negative one. If the charges were completely separated, this moment should be
D stands for Debye and equals 3.336Cm.
The value obtained experimentally is 1.83D. It means that the hydrogen does not totally give its electron to the fluorine. The ionic character of a liaison is given by
And if this value is over 50%, we consider that the liaison is an ionic liaison.
Fluorine has the highest electronegativity but has not a polarity large enough to have an ionic bond with the hydrogen (only 41.6%). The reason is that both H and F have a very small radius and that the liaison’s length is thus small and the liaison is strong. It is the reason why HF is a weak acid while the other acids of halogen are strong acids: the negative charge is more stabilised on Cl–, Br– and I– than on F–.
Note that a molecule that has polar bonds is not automatically polar CH4 is nonpolar. The polyfluorocarbon (CF2)n is nonpolar as well.
Polar molecules are soluble in polar solvents and nonpolar molecules are soluble in nonpolar solvents. In polar solvents, the acceptor and the donnor of electrons dissociate because the charges of the ions are stabilised by the solvent molecules (the solvation has been explained in the section on the nucleophile substitutions). For instance, when we put some NaCl into water, the salt dissociates into the ions Na+ and Cl–. If this salt is put in a nonpolar solvent, NaCl remains as one molecule.
On jackets, nonpolar molecules are grafted so that rain does not penetrate the jacket but can only roll on it. On a nonpolar surface, water does not spread but restricts its surface at the maximum, forming a sphere.
Rule of the octet and formal charge
Through bonding, atoms try to have 8 electrons of valence, the electronic configuration of noble gases. For example CaCl is not a correct molecule. Ca has 2 electrons of valence and Cl has 7. To bind, Ca gives one electron to Cl. Cl reaches the octet but Ca has still one electron of valence to lose. The correct formula is CaCl2: Ca gives one electron to two Cl to reach the electronic structure of the noble gas Argon.
In CO2, the liaisons are covalent and the electrons are shared between C and O. CO2 could possibly have two structures:
One can see that the oxygen’s of the molecule of the left are not equivalent. In a molecule, the electronic distribution has to be the most homogeneous possible. Each atom has a formal charge (FC)
Let’s check the FC of each atom:

In the molecule of the right, atoms don’t have formal charges and this molecule is thus more stable than the molecule of the left, where charges are separated. In fact, the first molecule is a resonance form (i.e. a structure with the same composition but a different electronic repartition), but less stable, of the second molecule:

The rule of the octet works very well for the three first lines of the Mendeleev table. After that, some empty nd orbitals can be used to bind atoms. For example S can bind 6 atoms of fluor (SF6).
Now, is that molecule really linear, as we draw it? To determine the spatial structure of a molecule, we have to consider the atomic orbitals of each atom and the fact that liaisons are repulsive between each other (they are densely negatively charged). CO2 is thus linear, having an angle of 180° between the two double liaisons to reduce the repulsion between them. CH4 is a regular tetrahedral, having an angle of 109° between each liaison:
The black triangle is a liaison going in the direction of the reader and the dashes represent a liaison goind in the opposite direction.
The lone pairs also take space in a molecule. In fact, they take more space than a normal liaison: the electrons are piled up near the atom. As a result, H2O is not linear but is a tetrahedral. Yet, it is not a regular tetrahedron as the angle between the lone pairs (>109°) is greater than the distance between the liaisons (<109°). NH3 is tetrahedral as well but has the specific particularity that it quickly oscillates between two equivalent forms:
Hybridisation
We have seen earlier the forms of atomic orbitals (AO) and none of them was tetrahedral. The atomic orbitals mix together to form new molecular orbitals (MO) that are used to bind with other atoms. It is the hybridisation process.
One of the molecular orbitals is outlined in red for convenience. These hybrid orbitals are the result of the hybridisation of the atomic orbitals s and p. The orbitals ns and np have different energies and merge into molecular orbitals sp of equal energies. Only the last layer of orbitals (with exceptions) merge to form a new set of orbitals. The inner orbitals are not modified as shown for NH3 next:
N has 5 electrons of valence: 2 in 2s and 3 in 2p. They merge into 4 sp3 orbitals of equal energy. The exponent 3 on the p indicates that 3 orbitals p were merged with one (not indicated as an exponent) orbital s. As usual, the electrons are placed on all the orbitals before being paired. One orbital contains 2 paired electrons already: it is the lone pair. The three other sp3 orbitals contains 1 electron each. The hydrogen will bring one additional electron on those orbitals to bind and form NH3.
We can do the same for H2O:
The oxygen has one more electron than the nitrogen. It results in a second lone pair and only 2 hydrogen’s binding to O.
For SF6, two empty 3d orbitals are used.
Four of the six liaisons are in the same plane and the two others are on each side of this plane. SF6 has thus a octahedral structure.
Bonding and antibonding orbitals
When two atoms are approaching each other, their outermost atomic orbitals interact to form molecular orbitals. We have seen earlier bonding orbitals but it is not the only possible combination of orbitals that can take place. The combination can either be positive or negative.
Li2 combines the 2s orbitals of each atom. The positive and negative combinations of the wave functions give
If we put this to the square, we obtain the probability of presence of the electrons. In the case of the negative combination, one can see that between the atoms, there is a point where the probability of finding electrons in null. It leads to an antibonding orbital. In the case of the positive combination, the probability of finding electrons between the atoms is high everywhere. It leads to a bonding orbital. Bonding orbitals are stable and lead to a persistent liaison. Antibonding orbitals are unstable and liaisons are not made. We denote those orbitals with a *. The molecular orbitals resulting from ns orbitals are called sigma σ:
The same kind of bonding and antibonding orbitals exist for the np, nd and nf orbitals. The np orbitals in the direction of the liaison form a sigma orbital and the other np orbitals are responsible for the double and triple liaisons and are called liaisons pi.
The molecular orbitals have different energies and we will now explain how to determine which orbitals are used and which ones are not.
The atomic orbitals of the two atoms are placed on the left and on the right. On the middle, we place the molecular orbitals that result from the atomic orbitals.
Each orbital gives one bonding and one antibonding molecular orbital. The molecular orbitals are placed from bottom to top, going from the less energetic to the most energetic orbital. For Z<8, the MO π2p and σ2p are inverted: the MO σ*1s and σ2s are repulsing each other. To determine the energy of a molecular orbital, we use the linear combination of atomic orbitals (LCAO) method. This method will not be explained right now, but probably in the second or third year lessons. Yet, as it is a linear combination, the average energy of the molecular orbital obtained from atomic orbitals equals the average energy of those atomic orbitals. For example, the energy of the molecular orbitals σ2s+ σ*2s equals the energy of the atomic orbitals 2s+2s. It is also the case when the atomic orbitals don’t have the same energy.
The second step is to distribute the electrons on the MO. The electrons are distributed from bottom to top and each molecular orbital accepts 2 paired electrons.
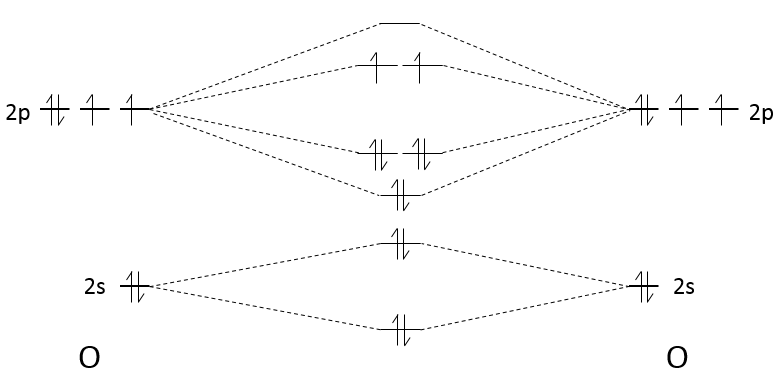
The effect of building those molecular orbitals is that the energy of the electrons has been decreased: only 2 electrons have a higher energy than the 2p orbitals but 6 have a smaller one (not counting the electrons from the 2s orbitals). The order of the liaison gives a good idea of the strength of the liaison and is given by:
The order tells us that the liaison between two oxygen’s is a double liaison. When the order of liaison is great, it means that the liaison is energetic and short.
Magnetism
Magnetism is the reaction of a particle to a magnetic field. As a reaction to a magnetic field, a particle orientates against the magnetic field or in its direction. This behaviour depends mainly on the electronic structure of the particle and on the temperature.
Diamagnetism
Diamagnetism is the opposition of any particle to a magnetic field. It appears in all materials but is very weak with regards to other magnetic behaviours. As a result, it is only observable in purely diamagnetic materials. To be so, a diamagnetic material has all its electrons paired. The opposite spins of paired electrons cancel the intrinsic electron magnetic moment: electrons are charged species revolving in one direction (spin) around the nucleus and can interact with an external magnetic field.
Paramagnetism
Unpaired electrons line up with a magnetic field and orientate particles in the same direction that the magnetic field. However, when the external field is removed, the particles do not retain the magnetic properties.
Ferromagnetism
It is the strongest reaction to a magnetic field and is the property of magnets. As for paramagnetism, unpaired electrons line up with a magnetic field but an additional effect exists for ferromagnetic particles: the aligned, adjacent particles exhibit a magnetic dipole-dipole interaction. Under certain conditions, the orbitals of their unpaired electrons can overlap. As a result, a similar effect than the exclusion of Pauli applies: it reduces the electrostatic energy of the electrons when their spins are parallel and not anti-parallel. The difference of energy between the parallel state and the anti-parallel state is called the exchange energy and defines the strength of the ferromagnetism of a particle.
Colour
The colour of compounds comes directly from the difference of energy between the highest occupied molecular orbital (=HOMO) and the one above it (=LUMO, lowest unoccupied molecular orbital). The molecule absorbs light to excite one electron. To jump by one level, the photon must have the same energy that the difference of energy between the levels. It means that only the light of a given colour is absorbed. Because this colour is absorbed, we don’t see it but see the colours that are not absorbed by the molecule.
Fluorescence is the light emitted when an excited electron de-excites to an intermediate level instead of its fundamental level. The emitted colour is thus different than the one absorbed and the process is very slow.
Metallic liaisons
In a metal, all the atoms are bound together. The molecular orbitals merge into a continuum band of conduction. As a result, the electrons are shared by all the atoms in the metal and electons can move along the metal. It is why metals conduct electricity.
Coordinative liaisons
Coordinative liaisons are liaisons made when an atom wearing one (or more) lone pair of electrons uses one pair to bind a cation.
The two electrons of a coordinative liaisons come both from one atom. The geometry of the molecule does not change when a coordinative liaison is made and the liaison has to be at the initial position of the lone pair.
In hydrogen bonds, the cation is a proton. These liaisons are weaker than a normal covalent liaison but can have an important role in the structure of a compound.
For example, the difference between ice and water is the proportion and the arrangement of the hydrogen bonds. Indeed, the hydrogen bonds are working in synergy to strengthen the structure. There is a restriction for the angle between the hydrogen bond and the other liaison of the hydrogen, which depends on the compound. The presence and absence of hydrogen bonds have a big responsability in the structure, and thus the effectiveness, of proteins.
The cation can also be a metal of transition. In this case, the bonding molecule is called a ligand. The ligand will target the empty nd orbitals of the metal. The geometry of the resulting compound is tetrahedral or octahedral depending on the generated molecular orbitals.
The atomic orbitals nd splits into two levels of different energy. The lower energy orbitals are dxy, dxz and dyz for the octahedral structure and the orbitals dx2-y2 and dz2 have a higher energy.
It is the opposite for the tetrahedral structures.
The chemistry of coordination is a complex domain of the chemistry and it will be discussed in details in the courses of second year.
Exercises
1. What is the formal charge of the atoms with a *?
2. Which of those diatomic molecules are paramagnetic and what is their order of liaison? O2, N2, C2, F2, B2
3. What is the spatial structure of these molecules?
CO2, NO2, H20, CH3+, C2H6, BF3, C2H2, HCN
4. Explain why SiF4 is nonpolar while the liaison Si-F is polar.
5. Do these molecules have a dipolar moment? CCl4, HCl, F2, CO2, H2O, (C2ClH3)n
6. Why is the angle of liaison in SCl2 equal to 101°?
7. What is the hybridisation of the underlined atoms in these molecules? What is the spatial geometry around them?
H2O, XeF4, PCl5
Answers
1.
Butyric acid: FCO*=6-4-4/2=0
Carbocation: FCC+*=4-0-6/2=1
Pyrrole: FCN*=5-2-6/2=0
Potassium permanganate: FCMn*=7-0-14/2=0
Chlorous acid: FCCl*=7-4-6/2=0
Thionyl chloride: FCS*=6-2-8/2=0
2. Let’s focus on O2 and then extend the reasoning to the other species. Each oxygen atom has 6 electrons of valence. To determine if a molecule is paramagnetic, we need to know if there are unpaired electrons. To do so, we apply the LCAO (linear combination of atomic orbitals).
There are 2 unpaired electrons in the π*2p orbital. O2 is thus paramagnetic. The order of the liaison is given by
For the other species, we can do the same thing. Nitrogen has one valence electron less than the oxygen. The π*2p orbitals are thus unoccupied and N2 is not paramagnetic. The order is (8-2)/2=3.
C2: paramagnetic, order: 2
B2: not paramagnetic, order: 1
F2: not paramagnetic, order: 1
3. CO2: linear
NO2: linear
H20: bend
CH3+: planar
C2H6: tetrahedral
BF3: planar
C2H2: planar
HCN: linear
4. The dipolar moments of the liaisons cancel each other.
5. CCl4: No
HCl: Yes
F2: No
CO2: No
H2O: Yes
(C2ClH3)n: Yes
6. The S atom has 6 valence electrons, as the oxygen does. It means that S has a sp3 configuration with 2 liaisons and 2 lone pairs. The normal angle between liaisons for the sp3 configuration is 109.5° and there is a smaller angle in SCl2 because lone pairs take more space than liaisons because electrons are packed nearby the atom.
7. H2O: sp3
XeF4: sp3d2
PCl5: sp3d
Chapter 2: Periodic table of elements
The table of Mendeleev is also called the periodic table of the elements. More than a simple list of the existing atoms. Mendeleev sorted the elements with regard to their oxidation/reduction by O/H
R20 R0 R302 RH4 RH3 RH2 RH R
Where R is the element. The atoms of same oxidation were sorted by weight to obtain the different lines. Some holes were present in the table but it was assumed that the missing elements were not yet discovered. Scientists have been able to fulfil the periodic table by the artificial synthesis of those elements. In the table showed above, the elements from 110 to 118 are theoretical.
It may not look like, but the determination of this table was a huge improvement for the chemists. The table contains a gigantic number of information for each atom, but also shows some periodic trends.
One case
There is a large number of different models for the periodic tables. Some of them only show the symbol, name, atomic number (Z) and weight of each element but many other information can be displayed for each element. An example follows for the Aluminium.
Its symbol is Al, its atomic number is 13 and it has a weight of 26.981538 units of atomic mass (which is equivalent to the molar mass, in g/mol). The weight of an element is the average of the mass of its isotopes, taking in account their proportions. The weight is the property that we seek most of the times on a Mendeleev table. The number of electrons by layer can be determined from Z but is often indicated on the periodic table. Aluminium Z=13, meaning that the layer n=1 is complete with 2 electrons, the layer n=2 is complete with 8 electrons (2 in 2s2 and 6 in 2p6) and that 3 electrons are to be distributed in the n=3 layer. The 2 first electrons are in 3s2 and the last electron is in a 2p orbital. From that, we can determine that Al is on the third line of the table (n=3), in the third column (3 electrons are in the last layer).
Aluminium has a unique oxidation state (OS) of +3 (to be seen in a next section). Elements after the third column can have several OS depending on how they use their electrons. Finally, some temperature are indicated to let us know in which state, solid, liquid or gaseous, the element is found at a given temperature.
Lines
Each line corresponds to a value of n. Because a layer of electrons is added for each line, the radius of the elements increases when we are descending in the periodic table. The number of elements in a line is not identical from line to line, because the orbitals p and d are not present in the first lines. One can also see two particular lines at the bottom of the table, the lanthanides and the actinides, corresponding at the elements possessing an outer nf orbital.
Columns
The elements on a same column have the same number of electrons of valence. Each column is called a family and has a particular name. The three first columns and the 5 last are denoted Ia, IIa, IIIa,…,VIIIa and contain the main elements. In between are the transition metals, noted Ib, IIb,…
Ia (except H): alkali metals: they are all shiny (but tarnish in the contact of air), soft, highly reactive metals (in sctp, standart conditions of temperature and pressure) and readily lose their outermost electron to form a cation. They form strong bases when bound to OH– (NaOH,KOH).
IIa: alkaline earth metals: they are all shiny and reactive (in sctp). They readily lose their outermost electrons to form a cation of charge 2+.
IIIa: icosagens or triels: the column of Boron and Aluminium. They have 3 electrons in their outermost layer. Aluminium is one of the rare metals to have a low density.
IVa: crystallogens or tetrels: the group of the carbon and of the silicon. They have 4 valence electrons. Carbon is the essential component of living bodies (~23% of a human) but it is also a constituent of the earth through carbonates, and of the atmosphere through CO2. It is very resistant to heat. Silicon is a major constituent of the earth, second in abundance there. Si and C are in the same column but are surprisingly different. One of their common properties is that they can make long chains (C can make chains much longer than Si though). C can form pi liaisons while Si cannot because its radius is too large (no possible superimposition of the orbitals). CO2 is a gas while SiO2 is a solid (quartz) that is the base of the glass materials.
Va: pnictogens: the group of the nitrogen and of the phosphorus. 5 valence electrons, with two paired. They form stable covalent liaisons and can form double and triple liaisons. This ability to form persistent liaisons is the source of the toxicity of some elements of this group (arsenic, antimony). On the other hand, N2 is an inert gas which represents 78% of the air.
VIa: chalcogens: The group of the oxygen and of the sulphur. Oxygen has very different properties than the rest of this group: they are soft and do not conduct heat well. Oxygen makes up 21% of the atmosphere by weight, 46% of the earth’s crust by weight and 65% of the human body. Oxygen also occurs in many minerals, being found in all oxide minerals and hydroxide minerals, and in numerous other minerals. Ozone is spontaneously formed in the high atmosphere where it catches UV rays from the sun.
The emitted radical will react immediately with an adjacent molecule. The ozone is a better oxidant than O2 because a pi liaison is delocalised. As a result, ozone is often used to kill bacteria’s without waste.
VIIa: Halogens: All the halogens form acids when bound to a hydrogen and are generally toxic. They also from salts when bound to alkali’s.
VIIIa: Noble gas/Rare gas: those element are inert: they do not react with any other element. Helium is the most common element in the universe (~24% of its mass). Because of their lack of reactivity, there are used in lighting (also true for nitrogen)
Metals, metalloids, nonmetals
The periodic table can be divided in three broad sections: metals, metalloids, nonmetals. These three categories are well regrouped in the table (except H, as always). Most of the elements are metals. The nonmetals are on the top right corner of the table (+H) and metalloids are only the elements on a diagonal from Boron to Polonium.
Metals
Metals have good thermal and electrical conductivity. As a broad category, they have common properties but exceptions exist for several elements for one or more properties.
They have in general a low ionisation energy, a low electronegativity and give or share their electrons when bonding. The bonding of two or more metals forms an alloy. Most of them can form oxides and are naturally found in this state.
In general, they are soft and malleable solids of high density but some are liquids in sctp (Hg for example). Most of them are silvery coloured.
Nonmetals
Most of nonmetals are low density gases in sctp. When bonding, they share or accept electrons and do not form basic oxides (but well acidic oxides as HClO, H2SO4, etc). In opposition to metals, they do not conduct electricity or heat well, and have a high ionisation energy and electronegativity. Usually, they are not naturally found in a combined state.
Metalloids
They are the minority of the elements. They look like metallic solids and can form oxides (acidic, basic or amphoteric). Most are semiconductors, and moderate thermal conductors, and have structures that are more open than those of most metals.
Periodic properties
Atomic radius
Several kinds of radius can be determined for a single element.
Crystalline radius: a crystal is a solid in which the atoms are spatially arranged. Monocrystals are obtained from the aggregation of atoms on one unique atom. They have the advantage of having less defaults in their structure than crystals arranged around several sources. Crystals are not necessarily a structure made of a single element. It is for example usual to make crystals from proteins to determine their spatial structure.
The method to obtain crystals is as follows: the element of the crystal is first dissolved in a solvent. The dissolution can be helped by an increase of the temperature. Once the dissolution is complete, the goal is to decrease very slowly the affinity of the element with the solvent. It can be done through the evaporation of the solvent (another solvent of lower affinity replaces the evaporated solvent) or if the solution was heated, through a slow decrease of the temperature. The process has to be slow to avoid the formation of several centres of aggregation.
The structure of the crystals and the distance between atoms inside a crystal depends on its constitutive elements and can be determined by RX diffraction.
In this method, a RX beam hits the surface of a crystal with a given angle θ.
The interaction of this beam with the atoms of the first layers of the crystal. This interaction gives place to diffraction only if
Where d is the distance between layers in the crystal, θ the angle of incidence and λ the wavelength of the beam. This equation is the equation of Bragg. If this condition is not fulfilled, the interaction between the atoms and the beam are destructive (i.e. they are cancelling each other) and no diffraction occurs. The radius is the half of the distance between atoms in the crystal.
Calculated radius: we consider here that the radius for which the probability of presence of the electron is the largest is the radius of the atom.
Van der Waals radius: The van der Waals radius is obtained by the addition of the repulsive force and the attractive force between two atoms. These two forces depend on the distance separating the atoms but not the same way. The attraction is proportional to the radius power -7 while the repulsion on the radius power -13. As a result, there is a favoured distance between the atoms when they bind. It is the attraction pit. Reducing this distance increases drastically the potential energy. σ is the distance of smallest approach and is the crossing between the curve and Epot=0. Increasing the distance also increases the potential energy towards 0.
The radius of the atom can be determined from σ.
Covalent radius: for diatomic molecules, the radius of the atom is considered as the half of the liaison’s length.
Empirical radius: it is obtained from the volume of the atomic gas. In a given volume of gas, there is a given number of atoms. Considering spherical atoms, the volume of one atom is V=4/3π r3. Therefore the radius is determined.
Those different radius are not equals and in some case they do not exist. For example, there is no covalent radius for He.
However, each of them follows the same logical repartition in the periodic table:
As we have seen in the previous section, a layer of electrons is added at each new line of the periodic table. It is thus logical that the radius of the elements increases in a single column. Moving across a line, the number of protons in the nucleus increases and the outer electrons are thus more and more attracted by the nucleus. From left to right, the radius decreases. As a result, Li and Mg have a similar radius, as do Na and Ca.
Ionisation energy
The ionisation energy (IE) is the energy required to remove one electron from an atom of a gas.
This energy is positive (atoms in gas don’t lose their electrons spontaneously) and depends on the energy of the electron: an electron close to the nucleus is hard to remove. It is also way more difficult to remove a second electron from an atom which had already lose one. For example, the aluminium has the following ionisation energies:
The first electron is relatively easy to remove: it is the single electron on the orbital 3p of the aluminium. The next electron is way more difficult to remove: it is an electron on a complete orbital. The third energy of ionisation is small for a third ionisation: we obtain the electronic structure of the noble gas Neon: the octet is complete and this structure is stabilized. This stabilisation is visible in the next energy of ionisation: a gigantic energy is required to remove one additional electron.
The energies of ionisation are periodic on the Mendeleev table. It requires a massive energy to remove an electron from a noble gas but it is easier to go towards its electronic structure. In one period/line, one can see that the trend of the IE is not linear. It is more difficult than average to remove an electron from a complete orbital
It is easier to remove one paired electron (less repulsion)
It is easier to empty one orbital: the last electron is shielded by the electrons of inner orbitals.
For the same last reason, the IE decreases when moving downwards in the periodic table: the shielding effect is bigger and bigger with the number of layers of electrons.
Electroaffinity
The electroaffinity is just the opposite of the ionisation: it is the energy required by a gaseous atom to accept an additional electron and follow the opposite evolution than the IE.
Note that noble gases don’t have any electroaffinity because they are inert.
Electronegativity
The electronegativity is an important notion in chemistry: it is the ability of an atom to attract the electrons of a liaison it shares. The symbol for the electronegativity is χ.
Pauling determined that, by convention the fluor, being the atom of largest electronegativity, has χ =4. The other elements have an electronegativity given by
Where DXY is the energy of dissociation between X and Y, i.e. the required energy to break a liaison between X and Y.
The fluor being in the top right corner of the table, it is not difficult to understand the trend for the electronegativity.
Exercises
- What is the symbol, atomic number and weight of the following species?
Chlorine, silver, sodium, carbon, argon, neon, cerium, magnesium, oxygen, iron, tin, antimony
- Name the following species:
O2, NaCl, 10n, HNO3, SnBr4, 21H, P2O5, H2S, HClO2, CO2, HClO3, HNO2, HClO4.
- What is the molar weight of the above cited species?
- What is the formula of
Carbon monoxide
phosphorous acid
sodium bromide
dinitrogen trioxide
hydrogen peroxide
- How much perchlorate of calcium do we have to weight if we want 50 moles of it?
- How many molecules of AgI is there is 20g?
- Which element has a higher electronegativity?
- F or I
- Na or Cl
- Mg or Ar
- Which element has a higher energy of ionisation?
- I or Br
- C or F
- P or Na
- Which element has a larger radius?
- Al or S
- Li or O
- Sn or Rb
- Chlorine has two stable isotopes: 35Cl and 37 Their masses are 34.96885 and 36.96590. What are is the proportion of both of the isotopes knowing that the atomic mass of the chlorine is 35.4527?
- The mass of 0.1726mol of an acid HXO4 is 25g. Determine the element behind X.
- How many valence electron in halogens? In earth-alkalines?
- What are the names of those reactions?
Answers
- What is the symbol, atomic number and weight of the following species?
Chlorine, silver, sodium, carbon, argon, neon, cerium, magnesium, oxygen, iron, tin, antimony
- Name the following species:
O2: oxygen
NaCl: Sodium chloride
10n: neutron
HNO3: nitric acid
SnBr4: tin (IV) bromide
21H: deuterium
P2O5: phosphorus pentoxide
H2S: hydrogen sulphide
HClO2: chlorous acid
CO2: carbon dioxide
HClO3: chloric acid
HNO2,: nitrous acid
HClO4: perchloric acid
- What is the molar weight of the above cited species?
O2: 32g/mol
NaCl: 58.44g/mol
10n: 1g/mol
HNO3: 63.01g/mol
SnBr4: 438.33g/mol
21H: 2.01g/mol
P2O5: 141.95 g/mol
H2S: 34.08 g/mol
HClO2: 68.46 g/mol
CO2: 44.01 g/mol
HClO3: 84.46 g/mol
HNO2,: 17.18 g/mol
HClO4: 100.46 g/mol
- What is the formula of
Carbon monoxide: CO
phosphorous acid: H3PO3
sodium bromide: NaBr
dinitrogen trioxide: N2O3
hydrogen peroxide: H2O2
- How much perchlorate of calcium do we weight if we want 50 moles of it?Formula of the perchlorate of calcium: Ca(ClO4)2Its molar mass is: M=40.078g/mol+ 2x(35.4527g/mol + 4×15.9994g/mol) =238.9786g/molThus, 50mol of it weight 11.948kg.
- How many molecules of AgI is there is 20g?1 mol of AgI weights 234.77267g. There are thus 0.085mol of AgI in 20g. The question is how many molecules are in 20g of AgI. In one mole, there are NA (the Avogadro number=6.022 1023) molecules. That makes 5.13 1022 molecules.
- Which element has a higher electronegativity?
- F or I
- Na or Cl
- Mg or Ar (Ar is a noble gas, so it does not accept any additional electron)
- Which element has a higher energy of ionisation?
- I or Br
- C or F
- P or Na
- Which element has a larger radius?
- Al or N
- Li or O
- Sn or Rb
- Chlorine has two stable isotopes: 35Cl and 37 Their masses are 34.96885 and 36.96590. What are is the proportion of both of the isotopes knowing that the atomic mass of the chlorine is 35.4527?
To solve this, we have to consider 2 things:
- The atomic mass of an element is the average of the masses of its stable isotopes. So 35.4527=x 34.96885 + y 36.96590 where x and y are the proportions of each isotope.
- The sum of the proportions of the isotopes is 100%: 1 (100%)= x + y.
We have thus two equations with 2 unknowns. That can easily be solved:
The proportions are thus 24.23% of 37Cl and 75.77% of 35Cl.
11.We determine first the molar weight of the acid:
The mass of X is the molar weight of the acid minus the known atoms:
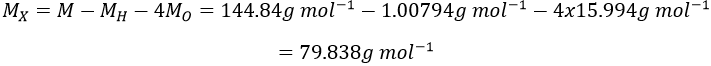
X is thus the bromine Br.
12. 7 in halogens, 2 in earth-alkalines
13.
Chapter 1: Electronic structure of atoms
Let’s resume what we know from the atoms: atoms can be broken and are composed of charged species – protons and electrons – and neutral particles – the neutrons. Atoms are different for each element (or isotope) by the number of those three species. A nucleus is at the centre of the atom and is surrounded by void and a cloud of electrons. The nucleus is made of neutrons and protons and makes the major part of the mass of the atom. However, the spatial distribution of the electrons is not random. Several planetary orbit theories were proposed after the works of Rutherford on the atomic nucleus but it is the Bohr’s model which can be considered as the first viable model. Some of the hypotheses of this model were not correct but it was the first step toward the understanding of the structure of an atom.
Bohr worked on the emission of light from dihydrogen H2. In an electric environment H2 dissociates in 2 excited H* that emit light to get back to its fundamental level.
hν is the usual way to represent a photon, emitted or absorbed during a physical or chemical process. h=6.626×10−34Js is the Planck constant. The emitted light has only a few selected wavelengths.
Based on that fact, he elaborated a model for the electronic structure of the atom. Unfortunately, the model only works for the Hydrogen and for the cation of He, i.e. atoms with a single electron.
Bohr used 4 postulates:
- electrons revolve on circular orbitals
- On a given orbital, an electron does not lose energy
- Gains or losses of energy correspond to the jump from one orbital to another one.
- Electrons are subject to a angular moment L
Bohr calculated the radius and the energy of the orbitals: to stay on a given circular orbital, the electron endures a centrifugal force (left part of the equation), which is counterbalanced by the attraction of the nucleus (right part)
where ε0 is the permittivity of the medium. As mvr=nħ, we can simplify the equations from the square of it:
Injecting the centrifugal force into the previous equation, we obtain an expression for the radius of an electron:
The energy of an electron is the sum of its kinetic energy and its potential energy. The potential energy comes directly from the Coulomb’s Force (remember that an energy is a force multiplied by a distance)
The radius was determined previously and can be used to determine the energy of an electron for a given atom
R is the constant of Rydberg and R=-2.178 10-18J.
To jump to an orbital of greater number/radius, an electron requires a given amount of energy, obtained from heat or light. Doing so, the electron is said excited.
To go back to its fundamental state, the excited electron frees the same energy in the form of a light of a given wavelength. The wavelength of the light is directly related to the difference of energy between the orbitals:
This kind of transition, from an excited level to the fundamental one is called a Lyman transition and emits in the UV wavelengths. If the destination level is not the fundamental one, others names are given:
The second hypothesis of Bohr was incorrect and electrons interact together.
To determine the correct form of orbital and the position of electrons, it is first necessary to develop quantum mechanics.
Quantum mechanics
An important principle of the quantum mechanics is the uncertainty principle of Heisenberg: it is impossible to determine at the same time the exact position and the exact movement of a particle such as an electron or a photon:
This relation means that we can only work with probabilities for an electron to be at a position. The electron is not considered as a point but as a stationary wave along its orbital.
The wave has a given number n (1, 2, 3,…) of fixed points, i.e. points where the wave crosses the theoretical position of the electron on its orbital. It is easier to explain this on a linear path but it works as well on a circular orbital. This number n will be useful later.
To determine the (probability of) position of an electron, we have to solve the equation of Schrödinger
Ĥ is the Hamiltonian operator and Ψ is the wave function, to be determined. To solve this equation, we use the particle in the box method: considering a square box of length L containing a particle, the probability to find the particle at a given place can be determined. In our case, the particle is an electron and the nucleus is in the centre of the box.
So, the relation to solve is
The fact that the second derivative of the function gives the function let us guess a sine or cosine function. The fact that it is negative indicates that it is a sine function. We will try a solution of the type
A and k will be determined later but do not depend on x. We can easily confirm our previous guess now:
As A does not depend on x, it can be placed out of the derivative without problem, and simplified with the other side of the equation
Giving us a relation for E
The values of k and of A will now be determined from the boundaries conditions of the box:
- The electron is not on the boundaries
- The electron is in the box. Its probability of presence Ψ2
From the first relation, we find the value of k:
Taking this into account, the second relation gives the value of A:
The integral of the sine equals 1, so the value of A is simply
The wave function is thus
The probability to find an electron at a given place is Ψ2(x):
As a result, for n=1, the probability to find an electron is the greatest at the centre of the box, i.e. close to the nucleus. For n=2, there is a fixed point at the centre of the box, meaning that the probability to be near the nucleus is null.
However, the volume near the nucleus is very limited and this parameter has to be taken in account. We use thus a radial probability of presence: Ψ2(x)4πr2 to obtain the distribution of electrons.
Depending on n, the (probability of) position of an electron can thus vary. For an increased n, the distance of the electrons increases but become closer and closer to each other (remember the figures of the Bohr model).
We won’t develop much more develop quantum mechanics in this section. One more notion is however needed to determine the number of electrons in the different orbitals: the quantum numbers.
Quantum numbers
There are 4 quantum numbers (QN)
- Principal QN: n=1, 2, 3,… this number defines the size and the energy of the orbital
- QN of angular moment: l.
L goes from 0 to n-1. Depending on the value of l, the orbitals are named s, p, d or f. The shapes of these orbitals are different:
- Orbital s
- Orbital p
Orbitals p are axial
- Orbital d
Orbital d are essentially biaxial. Two of them are on the axes and the three other are at 45° between axes
- Orbital f
Orbital f are polyaxial (and won’t be drawn here, sorry)
- Magnetic QN:ml
ml goes from –l to l and defines the orientation of the orbital
- QN of spin: ms
ms defines the spin of the electrons. Electrons can go in two opposite directions and ms= -½ or ½.
Electrons must have a different set of QN: it is the Pauli’s principle of exclusion. That means that an orbital can only accept a given number of electrons. There can thus only be 2 electrons of opposite spin for a given set of the three other QN. When the two electrons are together, we said that they are paired.
For example, there can be 8 electrons for n=2: l can have a value of 0 or 1
For l=0, the corresponding orbital is the orbital 2s. ml=0 and ms can either be ½ or -½. There are thus 2 electrons of opposite spin in the 2s orbital.
For l=1, the corresponding orbital is 2p. Three ml values are possible (going from –l to l): ml=-1, ml=0 and ml=1 (corresponding in the three Cartesian directions x, y and z). Each of those can accept an electron of spin ½ and -½. The orbital 2p can thus possess 6 electrons.
In total, 8 electrons can be placed for n=2.
If n=3, 10 additional electrons can be placed in the d orbital, for a total of 18.
All the orbitals don’t have the same energy. And electrons will first take place in the lower energy orbitals. Indeed, the external electrons are on more energetic orbitals: the inner sheets of electrons are shielding the charge of the nucleus and also have a repulsion effect on the external electrons.
The energy of orbital depends on n
E(n=1)<E(n=2)<….
But also on l
Ens<Enp<End<Enf
However, the global classification is more complicated than just all the orbitals of n=1, then of n=2, etc…
There is a method to remember the order in which we place the electrons on orbitals:
The electrons are placed following the arrows. 2 electrons can be placed on ns orbitals, 6 on np orbitals, 10 on nd orbitals and 14 on nf orbitals. This number is indicated on the figure on the top right for each set (n,l) of orbital. Two electrons are first placed on the 1s orbital, each with a different spin. The same is done in the orbital 2s. It takes less energy to place two paired electrons on the orbital 1s than one in the 1s and 2s orbitals. However in a same set of (n,l) it takes less energy to place one electron on each individual orbital. So, there are three orbitals in the 2p: 2px, 2py and 2pz. One electron is thus placed on each of those three orbitals and then electrons are paired.
There are some exceptions in this method due to the particular stability of d orbitals. d orbitals are the outer orbitals of the metallic atoms of transition. The d orbitals are very stable when they are complete or half complete, i.e. have 10 or 5 electrons. Electrons of lower orbitals can be displaced in the d orbitals to reach this quota. Let’s take a look on some metals to understand better this phenomenon.
The electronic configuration of V (Z=23) is
[Ar] 4s2 3d3
There is no need to write the complete configuration of atoms. The inner electrons don’t have any impact on the properties of the atom. Instead, we write the name of the previous noble gas between accolades. Argon (Ar) has Z=18 so there are still 5 electrons to place on orbitals. The first tow electrons are paired on the 4s and the three other are placed on 3 3d orbitals. Even if 4s has a bigger n, it is less energetic than 3d because of an effect of penetration (develop). There is nothing particular in this case.
The electronic configuration of Cr (Z=24), that has 1 more electron than V is
[Ar] 4s1 3d5
One electron has been taken from the 4s orbital to reach the half completion of the d orbitals. For Z=25 (Manganese, Mn), the 4s orbital receives the additional electron. The same phenomenon occurs for the copper Cu (Z=29) to obtain a complete 3d orbital:
Ni: [Ar] 4s2 3d8
Cu: [Ar] 4s1 3d10
On the periodic table of Mendeleev, a line begins when we place a first electron in a ns orbital. However, this is not this way that the table was developed initially. We will look closely at this table in the next chapter, explaining its shape, the elements and the general properties that can directly be related to the place of the element in the table.
Exercises
1. To which element corresponds this electronic structure:
1s2 2s2 2p4
[Ar] 4s2 3d6
[Ne] 3s1
2. What is the electronic configuration of Ar, Si, Cr, Nb, Al, F, Rb, Es?
Answers
1.
1s2 2s2 2p4 oxygen
[Ar] 4s2 3d6 Fe
[Ne] 3s1 Na
2.
Ar: [Ne] 3s2 3p6
Si: [Ne] 3s2 3p2
Cr: [Ar] 4s1 3d5
Nb: [Kr] 5s2 4d3
Al: [Ne] 3s2 3p1
F: 1s2 2s2 2p5
Rb: [Kr] 5s1
Es: [Rn] 7s2 5f11